GOS / 19 Основы СТО

19.Релятивистская механика. Постулаты Эйнштейна. Пространство-время, системы отсчета в СТО. Преобразования Лоренца и их кинематические следствия.

СТО была разработана Эйнштейном в 1905 г. В основе этой теории лежат 2 постулата:

1. постоянство ск-ти света в вакууме;

2. принцип отн-ти Галилея, распр-й на все физич. явл-я и процессы.

Сформ-ем эти постулаты.

1. Ск-ть света в вакууме не зависит от дв-я ист-ка света и от дв-я приемника света. Она яв-ся универсальной постоянной, равной с=3*10⁸м/с.

2. Принцип отн-ти Галилея в механике утверждает,что все инерциаль. с-мы равноправны с-ме закон-тей пртекающих механич-х явл-й и прцессов. Нходясь в ИСО, невозможно опр-ть, нах-ся ли эта с-ма в покое или дв-ся прямолинейно и равномерно. Если для этой цели иссл-ть закон-ти пртекания мех-х явл-й и процессов. Во всех с-мах эти явл-я и процессы протекают одинаково.

Эйн-н распространил прин-п отн-ти на все явл-я природы и на з-ны физики. Прин-п отн-ти в формул-ке Эйн-на:

1. Все явл-я физики пртекают в различных ИС одинаково. Иначе, наблюдая за явл-ями в одной ИСО, невозможно обнаружить равномерное и прямолин. дв-е.

2. При переходе с одной ИСО в др-ю необх-мо исп-ть преобразования корд-т и времени.

В механике Ньютона такими преобр-ями яв-ся преобр-я, выведенные Галилеем. Они назся преобр-ями Галилея. Рассм-м эти преобр-я.

Осущесвим синхронизацию часов в ИСО. По преобразованию Галилея

K’ =>K: x=x’+v_ot’ K=>K’: x’=x- v_ot

y=y’ y’=y

z=z’ z’=z

t=t’ t’=t

0: х=0

х’=- v_ot’

x=α(x’+v_ot’)

0’: x’=0

x= v_ot

x’=α’(x- v_ot)

K’=>K: v₌v_’+v_o, a=a’, m=m’, F=ma

K=>K’: v_’=v_–v_o, a’=a, m’=m, F’=m’a’

В соответствии с переходами Галилея вид з-нов Ньютона не изменяется. Иначе говоря, з-ны Ньютоновской механики инвариантны отн-но преобр-й Галилея.

В СТО преобр-я корд-т и времени при переходе из одной ИСО в другую имеет иной вид. Эти преобр-я корд-т и времени впервые были получены голландским ученым Лоренцем в 1904 г. Рассмотрим преобр-я Лоренца.

Рассм-м 2 ИС. Пусть напр-я осей х и х’ совпадают, пусть с-ма K’ дв-ся дв-ся отн-но К со ск-тью v_o, пусть осущ-на синхронизация часов.

0: х=0

х’=- v_ot’ => х’+v_ot’=0

x=α(x’+v_ot’) (a)

0’: x’=0

x= v_ot => x-v_ot=0

x’=α’(x- v_ot) (б)

Из принципа отн-ти следует равноправие всех ИСО, след-но, α’= α.

x=α(x’+v_ot’) (a₁)

x’=α(x-v_ot) (б₁)

Предположим, что в момент совпадения начал отсчета с-м в этом месте пропущена световая вел-на и световая волна распр-ся………………………………….Коорд-та фронта волны в той ……….. СО выразится след. образом:

x=ct, (в)

x’=c’t’ (г)

Из принципа постоянства ск-ти света следует c=c’.

x=ct, (в₁)

x’=c’t’ (г₁)

Теперь в₁ и г₁ подставим в а₁ и б₁.

x’x=α²(x’+v_ot’)(x-v_ot)

с²tt’=α²(сt’+ v_ot’) (ct-v_ot)

с²tt’= α²ct’(1+v_o/c)ct(1-v_o/c)

1=α²(1-v_o²/c²) => (1) (1a) (1б)

Выр-е 1б подставим в 1а, тогда получим: (2б). Или наоборот: .(2а)

Соберем все преобр-я и получим:

K’ =>K: K=>K’:

y=y’ y’=y

z=z’ z’=z

Учитывая совместно оба принципа СТО, получим преобр-я корд-т и времени, к-рые наз-ют преобр ями Лоренца.

З-н преобр-я ск-тей:

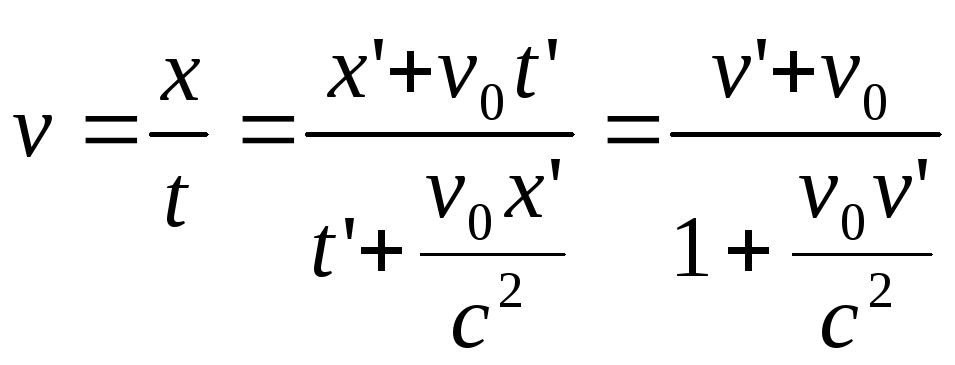(3) a=a’ (3a) a’=a

v – ск-ть дв-я тела в с-ме К, v’– ск-ть того же тела в с-ме К’, v_o– ск-ть дв-я с-м корд-т отн-но дуг друга, с – ск-ть света в вакууме.

Если дв-е тела происходит и v<c, то преобр-я Лоренца переходят в преобр-я Галилея и оказ-ся справедливыми все соотн-я Ньютоновской механики.

Выводы СТО, вытекающие из преобр-й Лоренца, имеют практич. знач-е только при дв-нии тел со ск-тями, близкими к ск-тям света.

Рассм-м вопрос о пространственно-временных соотн-ях, вытекающих из преобр-й Лоренца или действующих в СТО. Покажем, что

1. длина жесткого стержня измен-ся со ск-тью этого стержня и оказ-ся минимальной отн-но той СО, отн-но к-рой этот стержень покоится.

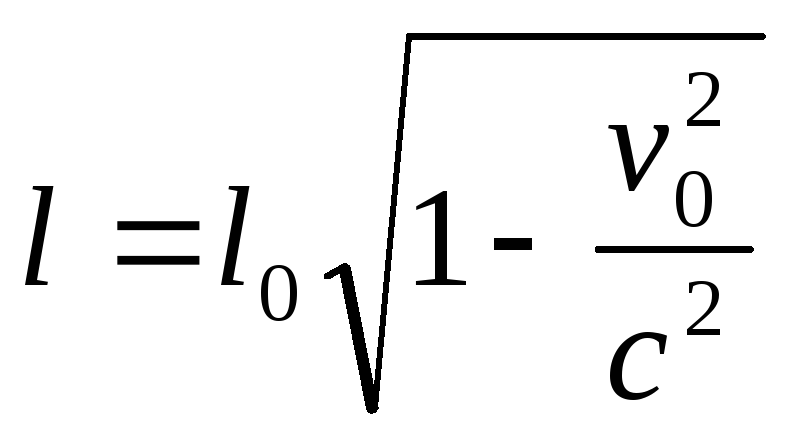
, l – длина жесткого стержня в той СО, отн-но к-рой этот стержень дв-ся со ск-тью v_o. l_o – длина стержня отн-но с-мы к-т, отн-но к-рой стержень покоится.

2. Пространственное разделение события: одновременное событие в одной СО не яв-ся одновременным в др-й СО, т.е. абсолютная одновременность пространственно разделенных событий места не имеет.

3. Длительность процесса не яв-ся абсолютной, а зависит от ск-ти дв-я в той точке, в к-рой этот процесс происходит. Длит-ть процесса минимальна в той СО, отн-но к-рой точка покоится. Все эти кинематические соотн-я, все эти пространственно-временные соотн-я имеют практич. знач-я только при дв-нии со ск-тями, близкими к ск-тям света.

, .

Это из процедур измерения длин жесткого стержня, движ-гося со ск-тью v_o, следует, что t₁=t₂=t.

Вычитая х₂’-x₁’ и приравнивая х₂’-x₁’=l_o, х₂-x₁=l, получим (4).

Преобр-я Лоренца требуют вывод, что абсолютная одновременность пространственно разделенных событий места не имеет. Простр-ное разделенные события, одновр-ные в одной ИСО, не яв-с я одновр-ми в др-й ИСО.

По усл-ю: t’₁=t’_2, х₂’-x₁’=l.

а) ; б)

;

=> (5)

Из преобр-й Лоренца следует, что длит-сть процесса (одного и того же) в разных ИСО оказ-ся различной. Она минимальна в той СО, отн-но к-рой точка, где происходит событие, покоится.

По усл-ю: t’₂–t’₁= τ₀, х₂’=x₁’= x’.

; ;

t₂–t₁= τ

=> (6)

Иллюстрацией соотн-я (6) яв-ся время жизни быстро летящих мюонов τ_о=2*10^-6с.

Из проебр-я Лоренца вытекают фундаментальные динамические и энергетические соотн-я. Рассм-м эти соотн-я.

(7) соотн-е массы-ск-ти.

m_o– масса тела (элем-й частицы) в той СО, отн-но к-рой эта частица покоится. Это масса «покоящейся» частицы.

m – масса того же тела (той же элем-й частицы) в той ИСО, отн-но к-рой частица дв-ся со ск-тью v_o. Это масса «движущейся» частицы.

; (8) – соотн-е импульс-ск-ть

– вектор импульса тела (частицы), движущейся со ск-тью v_o.

; (9) – соотн-е сила-ск-ть (2-й з-н Ньютона в СТО)

(10) Е – полная энергия тела (частицы)

Е= (10а) – соотн-е энергия-масса

Для покоящейся частицы полная энергия опр-ся соотн-ем .

Кин. энергия тела в СТО выр-ся как разность м/у полной энергией движущейся частицы и полной энергией покоящейся частицы: W=E-E₀, где W– кин.эн-я тела, дв-йся со ск-тью v_o.

(11)

При ск-тях дв-я, значительно меньших ск-ти света, формула (11) дает:

(11а) – при <<1 .

Получим важное соотн-е СТО м/у эн-ей и импульсом.; Е=.Возведем эти 2 ур-я в квадрат и поделим ур-е импульса на ур-е энергии. Получим .

(*) (12)

Поделим ур-е (*) на с² и получим: (13)

В соотн-нии (13) в првой его части произведение 2-х постоянных вел-н (с² и m_о²) яв-ся инвариантом в СТО, левая часть тоже яв-ся инвариантом в СТО. Т.е. это есть вел-на, к-рая с изменением ск-ти частицы остается постоянной. Меняются Е (полная эн-я), р (импульс), но их разность не меняется.

Все релятивистские соотн-я в СТО переходят в соотн-я Ньютоновской механики, если ск-ть дв-я тела мала по сравнению со ск-тью света в вакууме. Для макроскопических тел расположение дел справедливо всегда, но для микрочастиц ск-ти дв-я могут достигать значений, близких к ск-ти света, в этом случае соотн-я СТО яв-ся опр-щими базовыми соотн-ями.

Методика.

Изучение элементов теории относительности рекомендуют начинать с повторения того материала об относительности, который знаком учащимся, а именно: некоторые физические величины, характеризующие механическое движение и электромагнитное взаимодействие (координата, скорость, перемещение, импульс тела, кинетическая энергия, работа, индукция магнитного поля и т. д.), относительны, т. е. зависят от выбора системы отсчета, а другие (ускорение, заряд и т. д.) - инвариантны, т. е. не зависят от выбора системы отсчета; все законы механики справедливы относительно инерциальных систем отсчета и никаким механическим опытом, проводимым в данной системе отсчета, нельзя обнаружить, движется эта система равномерно и прямолинейно или покоится (принцип относительности Галилея). При повторении используют видеофильм «Относительность движения» и последнюю часть первого фрагмента видеофильма «Законы Ньютона», где иллюстрируется принцип относительности Галилея. После этого приступают к изучению специальной теории относительности.

Специальная теория относительности доказала, что законы электродинамики, как и законы механики, справедливы относительно любых инерциальных систем отсчета. А одновременно она явилась более глубокой теорией пространства и времени.

СТО построена по методу принципов, т.е. в основу ее кладут два постулата, которые опираются на опытные факты и, как исходные положения этой теории, ею не объясняются.

1) Все инерциальные системы отсчета равноправны; во всех инерциальных системах не только механические, но и все другие явления природы протекают одинаково (обобщенный принцип относительности Эйнштейна).

2) Скорость света с (в вакууме) одинакова во всех инерциальных системах отсчета и равна 3*10⁸ м/с.

В качестве опытного обоснования принципа относительности Эйнштейна следует рассмотреть опыт Майкельсона (его установку, идею, ожидаемый и полученный результат). Отрицательный результат этого опыта доказывает неправильность его исходной посылки о существовании абсолютной системы отсчета - эфира, в котором якобы развертываются все электромагнитные явления. Все инерциальные системы отсчета равноправны, законы природы в них одинаковы.

В качестве опытного обоснования второго постулата целесообразно рассмотреть движение двойных звезд.

Сложение скоростей. Закон сложения скоростей целесообразнее называть законом преобразования скоростей при переходе от одной инерциальной .системы отсчета к другой. Начать ознакомление школьников с этим законом целесообразно с создания проблемной ситуации, обратив их внимание на то, что постулаты СТО, на первый взгляд, противоречат друг другу. Действительно. одним из следствий принципа относительности в механике был закон сложения скоростей и вывод об относительном характере скорости. Между. тем второй постулат теории относительности утверждает: скорость света во всех инерциальных системах отсчета одна и та же, т. е. является величиной абсолютной. А. Эйнштейн доказал, что второй постулат не противоречит принципу относительности, просто закон преобразования (сложения) скоростей выглядит иначе.

В случае малых скоростей v<<c мы получаем закон сложения скоростей в механике.

Пусть система отсчета К' связана с вагоном, который движется относительно системы отсчета К со скоростью v . Предположим, в центре вагона находится источник света и его вспышка производит зашторивание окон, находящихся в противоположных концах вагона. В системе К', связанной с вагоном, окна по световому сигналу зашториваются одновременно, так как они находятся на равном удалении от источника.

Но с точки зрения наблюдателя, находящегося в системе отсчета К, относительно которого этот вагон движется справа налево, передняя стенка вагона удаляется от светового сигнала со скоростью v, поэтому сигнал проходит расстояние l/2+vt (l - длина вагона). Задняя стенка надвигается на него с той же скоростью v, поэтому путь, проходимый сигналом, будет равен l/2-vt.

В результате заднюю штору сигнал откроет скорее, чем переднюю. Пространственно разделенные события, одновременные с точки зрения наблюдателя в системе К', являются неодновременными с точки зрения наблюдателя К, относительно которого вагон движется. Итак, одновременность пространственно разделенных событий относительна.

Замедление времени. Для вывода соответствующей формулы вначале рассматривают движение светового сигнала в собственной системе отсчета и отмечают, что свет прошел путь L за время t₀ . Затем этот же процесс рассматривают с точки зрения наблюдателя, находящегося в системе отсчета К, относительно которой система отсчета К^/ вместе с вагоном движется со скоростью v.

Время 1₀, отсчитываемое в той системе отсчета, где происходит явление, называют собственным временем. Внимание школьников обращают на то, что в любой другой системе отсчета, движущейся относительно системы К, интервал времени больше (t>t₀) т.е. часы идут медленнее. В этом состоит релятивистский эффект замедления времени в движущихся системах отсчета.

Сокращение масштаба (преобразование длины отрезка при переходе от одной инерциальной системы к другой). При выводе относительности длины подчеркивают, что измерить длину отрезка - это указать одновременно координаты его начала и конца. Так как события, одновременные в одной системе отсчета, неодновременны в другой, то следует ожидать, что длина отрезка - понятие относительное. В мысленном эксперименте рассматривают измерение длины отрезка (линейки) с помощью световых сигналов, рассматривая распространение света от одного конца линейки и обратно с точки зрения наблюдателей из двух разных инерциальных систем отсчета: неподвижной системы К и системы отсчета К', связанной с самой линейкой и движущейся вместе с ней со скоростью v относительно системы К.

Анализируют полученную формулу. Из нее следует, что длина стержня относительна, она имеет наибольшее значение в той системе отсчета, где стержень покоится.

Зависимость массы от скорости. Масса является величиной относительной, зависящей от выбора системы отсчета. Если в системе, где тело покоится, его масса т₀ (масса покоя или собственная масса), то в любой инерциальной системе отсчета, движущейся со скоростью v, масса этого тела определяется формулой

Анализируя полученную формулу, указывают, что различие между массами т и т₀ заметно лишь при движениях со скоростями, приближающимися к скорости света.

Эта формула говорит также о том, что тела, имеющие массу покоя, не могут двигаться не только со скоростями v > с, но даже со скоростью v = с, ибо при этом масса становится бесконечно большой, что лишено физического смысла.

в самом общем виде навык определяется как «действие, сформированное путем повторения, характеризующееся высокой степенью освоения и отсутствием поэлементной сознательной регуляции и контроля». Навык можно расценивать как уровень совершенства действия, его качество. Поэтому формирование навыков является одной из самых важных проблем педагогической психологии.

Процесс формирования навыка включает определение его компонентов и такое овладение операцией, которое позволяет достичь наивысших показателей на основе совершенствования и закрепления связей между компонентами, их автоматизации и высокого уровня готовности действия к воспроизведению. Образование навыков характеризуется переходом от сознательных актов к автоматическим, и этот период сознательного усвоения имеет решающее значение для правильности и быстроты образования навыка.

По П. Я. Гальперину, процесс формирования навыков осуществляется более быстрыми темпами при использовании полной системы необходимых дидактических условий, обеспечивающих активный процесс формирования чувственных образов, понятий, умственных и перцептивных действий. Такая система открывает пути к систематическому применению проблемного обучения и намечает основные типы мотиваций в процессе обучения.

Мы полагаем, что основными психолого-педагогическими предпосылками формирования прочного навыка являются следующие:

а) целенаправленность обучения;

б) наличие у субъекта деятельности внутренней мотивации;

в) автономность обучающегося;

г) внутренняя системность – понимание, осмысление обучающимся выполняемого действия, полнота уяснения содержания операции;

д) уровень развития субъекта, наличие фоновых знаний и умений;

е) аффективный фактор;

ж) знание и оценка качества результатов выполнения действия.

Целенаправленность обучения предполагает четкую организацию учебного процесса, селективный подбор упражнений, нацеленных на выполнение конкретного действия, и их правильное распределение во времени обучения.

Итак, этапами организации предметных действий являются следующие: формирование системы понятий (знания) – автоматизированные умственные операции (навыки) – сложные умственные действия (умения).

Дидактический принцип системности и последовательности требует непрерывности функционирования триады «знания-умения-навыки», а анализ ее составляющих помогает выявлять оптимальные методы усвоения содержания изучаемых дисциплин и реально формировать высокий уровень профессиональной компетенции будущего специалиста.

Общее понятие о социальной педагогике как отрасли педагогического знания.

Социальная педагогика рассматривает процесс воспитания, социологию личности в теоретическом и прикладном аспектах. Она рассматривает отклонения или соответствия поведения человека под влиянием среды, то, что принято обозначать социализацией личности.

По современным представлениям социальная педагогика — это «отрасль педагогики, рассматривающая социальное воспитание всех возрастных групп и социальных категорий людей, в организациях, специально для этого созданных» [А.В. Мудрик].

По мнению В.Д. Семенова, «социальная педагогика, или педагогика среды, является научной дисциплиной, которая интегрирует научные достижения смежных наук и реализует их в практике общественного воспитания»2.Социальная педагогика опирается на историю педагогики, на опыт обучения и воспитания в прошлом, на практику воспитания и обучения в других странах.

Социальная педагогика — это самостоятельный раздел педагогики, со своими особыми методами социальной воспитательной и образовательной деятельности.

Методы социальной педагогики направлены на личность, ее самосовершенствование, самовоспитание, самоорганизацию, самоутверждение.

Прежде всего, надо определить, что такое социальная среда.

Это, во-первых, широкая социальная действительность, общество, государство и, во-вторых, это педагогики непосредственное окружение ребенка, влияющее на его формирование.

Социальное воспитание — понятие многомерное. Это забота общества о поколении будущего, поддержка человека обществом, коллективом, другим человеком, помощь человеку в усвоении и принятии нравственных отношений, которые сложились и семье и обществе, принятии правовых, экономических, гражданских и бытовых отношений. Помочь человеку — это значит научить его найти новый путь в своей жизни, суметь перестроиться в новой жизненной ситуации.

Термин социальная работа означает профессиональную деятельность по оказанию помощи человеку, группе, с тем ,чтобы улучшить их социальное положение.

Социально-педагогическая деятельность — это социальная работа, включающая и педагогическую деятельность, направленную на помощь ребенку (подростку) в организации себя, своего психологического состояния, на установление нормальных отношений в семье, в школе, в обществе.

Специфика объекта и предмета исследования социальной педагогики. Основные категории социальной педагогики (социальное обучение, социальное воспитание, социально-педагогическая деятельность, социализация, социум, институты социализации, социальная реабилитация, социальная адаптация).

Задачи, функции.

1.Первостепенной является изучение ребенка (подростка), его состояния, отношений в семье, в школе, с группой во дворе, его состояние в стадии конфликта.

Оказание помощи ребенку (подростку) попавшему в беду. Важно найти пути, варианты выхода из кризиса, поддержать в трудное время.

Анализ состояния социального воспитания в различных социальных сферах, окружающих ребенка и воздействующих на него.

Социальная педагогика призвана анализировать, обобщать и распространять, пропагандировать позитивный опыт.

Она должна направлять деятельность ребенка (подростка) на самовоспитание, самообучение и умение самостоятельно организовывать свою жизнь и поступки.

Социальный педагог занимается координацией и объединением различных специалистов, организаций, решающих проблемы ребенка (подростка), имеющих отношение к состоянию его кризиса, к защите его прав.

Одна из функций социальной педагогики сводится к организации исследований различных проблем социального воспитания, анализу работы социальных педагогов, коллективов, различных педагогических центров.

Таким образом, функции социальной педагогики можно сформулировать следующим образом, включив те, что перечислены выше. Это:

• воспитательная,

• социально-правовая,

• социально-реабилитационная.

Воспитательная функция предполагает включение ребенка в окружающую его среду, процесс его социализации, его адаптацию в ходе обучения и воспитания.

Социально-правовая означает заботу государства о детях, их правовую защиту.

Социально-реабилитационная функция — это воспитательная и образовательная работа с детьми-инвалидами, физически или психически неполноценными, где основные социальные функции, выполняет педагог.

Отсюда вытекают прикладные задачи социальной педагогики, на что ориентируется и, в соответствие с чем строит свою работу социальный педагог, социальный работник.

Прикладные задачи социальной педагогики

Одна из прикладных задач педагогики состоит:

Воспитывать в сознании ребенка понятия добра и справедливости, любви к ближнему, ко всему живому, творчеству, взаимопониманию.

Поставить цель самостоятельно выйти из кризиса, наметить пути выхода, научиться общению с окружающими людьми, определить цель и смысл жизни.