
GOS / 9 Электрическое поле
.doc8. (18).1)Охарактеризовать систему знании об электрических зарядах и их взаимодействии. Понятием «электрический заряд», так же как и понятием электромагнитное поле», учащиеся овладевают постепенно по мере изучения электродинамики.
Школьникам сообщают, что заряд - количественная мера способности тел к электромагнитным взаимодействиям. При этом следует обратить их внимание на то, что термин «электрический заряд» употребляют в различных смыслах: как термин, равнозначный выражениям «заряженная частица», «заряженное тело», для обозначения физической величины.
Еще в базовом курсе физики учащиеся узнали о фундаментальном свойстве - о существовании зарядов двух видов, причем заря-1ы одного знака отталкиваются, заряды разных знаков притягиваются друг к другу. Очень важно разъяснить, что электрический заряд не тождествен веществу. Заряд всегда связан с материальным носителем - телом или частицей. Электрический заряд - неотъемлемое свойство некоторых элементарных частиц. Не существует заряда без материального носителя, хотя нейтральные элементарные частицы есть (нейтрон и др.).
При анализе опыта Иоффе-Милликена показывают, что электрический заряд дискретен, он может принимать строго определенные значения. Школьники должны знать: вся современная физика приводит к выводу о существовании атома электричества - элементарного заряда. Есть много доказательств дискретности заряда. Сейчас их ознакомят с одним из них, в дальнейшем они узнают о других. Необходимо подчеркнуть также, что дискретность заряда элементарных частиц - проявление одной из существенных особенностей микромира. Далее школьники узнают, что в микромире дискретность присуща и ряду характеристик движения, например энергии. Это создает некоторую основу для восприятия в дальнейшем идеи квантования в атомной и ядерной физике.
У чащиеся
обязательно должны запомнить округленные
значения элементарного заряда и массы
покоя электрона: е= 1,6-10-19 Кл, me=9,1*10-31кг.
чащиеся
обязательно должны запомнить округленные
значения элементарного заряда и массы
покоя электрона: е= 1,6-10-19 Кл, me=9,1*10-31кг.
Полезно обсудить в процессе изучения электродинамики разные методы измерения заряда, например с помощью опыта Милликена или силы Лоренца; путем измерения силы тока и времени его протекания; на основе электролиза и др.
Школьникам разъясняют, что электрический заряд макроскопического тела равен сумме положительных и отрицательных зарядов частиц, входящих в состав данного тела. В обычном состоянии большинство тел электрически нейтральны, то есть число электронов в них, равно числу протонов. Нейтрален и атом любого вещества. Таким образом, положительно и отрицательно заряженные частицы в веществе связаны и образуют нейтральные системы. Чтобы получить заряженные макроскопические тела, необходимо нейтральные тела наэлектризовать, т. е. отделить часть отрицательного заряда от связанного с ним положительного. Рассматривают способы электризации. Макроскопическое тело можно зарядить двумя способами: электризацией трением (вернее сказать, соприкосновением) или электризацией через влияние.
Центральное место в разделе «Электродинамика» при изучении электрических зарядов занимает закон сохранения электрического заряда, который подтверждается всеми без исключения наблюдениями, проводившимися до сих пор. В старших классах возможна формулировка этого закона, которая учитывала бы атомистическое представление о строении электричества: в изолированной системе алгебраическая сумма зарядов всех частиц остается постоянной, заряженные частицы могут возникать вновь, но всегда рождаются парами: с одинаковыми по модулю и противоположными по знаку зарядами. Исчезают заряженные частицы тоже парами, превращаясь в нейтральные. Наряду с данной формулировкой можно дать и другую - макроскопическую, основанную на идее возможности измерения заряда: алгебраическая сумма зарядов в замкнутой системе остается неизменной во времени.
Школьникам дают возможное здесь доказательство справедливости закона сохранения заряда: одновременное появление противоположных по знаку, но равных по модулю зарядов при контактной электризации тел. Позднее они узнают о появлении двух противоположно заряженных частиц в процессе рождения электронно-позитронной пары, а также о превращении электронно-позитронной пары в фотоны, что также является доказательством этого закона. Можно рассказать еще, что любые процессы электризации тел (через влияние, химическая электризация в гальваническом элементе, фотоионизация и др.) сводятся по существу к разделению равных по модулю зарядов с противоположными знаками. Но не менее важно уяснить еще одно свойство заряда - его инвариантность, т.е. независимость модуля заряда от скорости движения заряженной частицы, а значит, и от системы отсчета. Школьникам объясняют, что закон сохранения электрического заряда тесно связан с инвариантностью заряда. Если бы величина заряда зависела от его скорости, то, приведя в движение заряды какого-нибудь одного знака, мы изменили бы суммарный заряд изолированной системы.
Таким образом, заряд не только сохраняется, но и не зависит от системы отсчета, он инвариантен. В этой связи надо заметить, что школьники часто отождествляют понятия «сохранение величины» и «инвариантность величины». Полезно обратить их внимание на то, что это не одно и то же: величина может сохраняться и, тем не менее, не быть инвариантной. Например, для таких величин, как энергия, масса, импульс, справедливы законы сохранения, и в то же время они изменяются при переходе от одной системы отсчета к другой, т. е. они не инвариантны. Все электромагнитные явления протекают так, как должно быть при абсолютности зарядов. Это является подтверждением принципа абсолютности (инвариантности)заряда.
Основные знания, которые должны приобрести школьники о взаимодействии зарядов, сводятся к следующему. Для неподвижных заряженных тел сила взаимодействия определяется законом Кулона. В случае движущихся зарядов сила электромагнитного взаимодействия существенно зависит от модуля и направления скорости. Соответственно электромагнитное взаимодействие как бы состоит из двух компонент: электрической и магнитной. Лишь в отдельных случаях (в некоторых системах отсчета) электромагнитное взаимодействие носит только электрический или только магнитный характер. Но поскольку скорость тела зависит от системы отсчета, то взаимодействие, его характер определяется системой отсчета.
Принципиально важно все время подчеркивать: взаимодействие между заряженными телами (частицами) осуществляется через поле. Заряженные тела (частицы) непосредственно друг с другом не взаимодействуют.
2 )
Электрическое поле в вакууме. По
современным представлениям атомы и
молекулы, состоящие из атомов, состоят
из электрически заряженных частиц. Атом
= ядро + электронная оболочка; ядро:z
протонов + (A-z)
нейтронов; протон: элементарный
положительный заряд; qp=+e=1,6*10-19
Кл, где z
порядковый номер элемента в таблице
Менделеева. Единицей электрического
заряда в системе СИ является 1 Кл(большая
величина статического заряда). Основной
силовой характеристикой электрического
поля окружающий электрически заряд
является напряженность.
)
Электрическое поле в вакууме. По
современным представлениям атомы и
молекулы, состоящие из атомов, состоят
из электрически заряженных частиц. Атом
= ядро + электронная оболочка; ядро:z
протонов + (A-z)
нейтронов; протон: элементарный
положительный заряд; qp=+e=1,6*10-19
Кл, где z
порядковый номер элемента в таблице
Менделеева. Единицей электрического
заряда в системе СИ является 1 Кл(большая
величина статического заряда). Основной
силовой характеристикой электрического
поля окружающий электрически заряд
является напряженность.![]() –
вектор напряженности электростатического
поля. Пространство окружающее электрический
заряд находится в особом состоянии. Это
состояние проявляется в том, что на
помещенный в данную точку поля пробный
электрический заряд действует сила.
Пробный заряд должен быть малой величины,
чтобы введение такого заряда не исказило
электрическое свойство среды. По
определению напряженность электрического
поля равна силе, действующей в данной
точке поля на единичный положительный
пробный заряд.
–
вектор напряженности электростатического
поля. Пространство окружающее электрический
заряд находится в особом состоянии. Это
состояние проявляется в том, что на
помещенный в данную точку поля пробный
электрический заряд действует сила.
Пробный заряд должен быть малой величины,
чтобы введение такого заряда не исказило
электрическое свойство среды. По
определению напряженность электрического
поля равна силе, действующей в данной
точке поля на единичный положительный
пробный заряд.
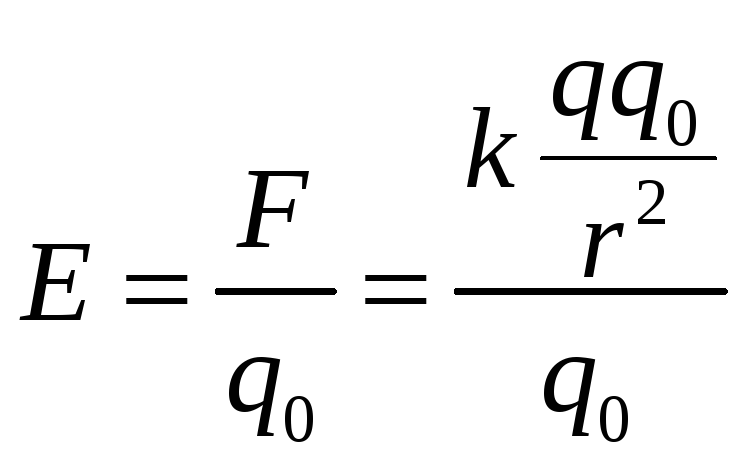
![]() ;
;
![]() ;
;
![]()
Обычно ЭП изображают посредством силовых линии или линии напряженности, при условии, что густота линии напряженности пропорциональна напряженности в данной точке поля.
Наряду
с напряженностью поля, которая является
важнейшей силовой характеристикой ЭП,
вводят понятие потенциал ЭП. Обозначается
φ. Она является энергетической
характеристикой ЭП.![]() или
или
![]() ,
где А-работа при перемещении заряда из
данной точки. Связь между напряженностью
ЭП и потенциалом:
,
где А-работа при перемещении заряда из
данной точки. Связь между напряженностью
ЭП и потенциалом:
![]() ,
,
![]() –скалярная
величина, а gradφ–
векторная.
–скалярная
величина, а gradφ–
векторная.
Принцип
суперпозиции.
Если в данной точке пространства
различные заряженные частицы создают
ЭП, напряженности которых
![]() и т.д., то результирующая напряженность
в данной точке равна
и т.д., то результирующая напряженность
в данной точке равна
![]() –
принцип суперпозиции.
–
принцип суперпозиции.
3) Теорема Остроградского-Гауса. Рассмотрим поле точечного заряда. Проведем сферическую поверхность с центром где расположен заряд.
Сферическая
пов.![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]() =
=![]()
![]()
![]() ,
[Ф]=В*м
,
[Ф]=В*м
Возьмем
площадку dS(см.
рис.)
![]() ,
,
![]() ,
,
![]()
![]() =
=
![]()
![]()
![]()
![]()
![]() ,
т.к.
,
т.к.
![]() ,
,
![]() ,
,
![]() .
Рассмотрим вопрос о величине потока ФЕ
через произвольную замкнутую поверхность.
.
Рассмотрим вопрос о величине потока ФЕ
через произвольную замкнутую поверхность.
проведем
элементарный телесный угол
![]() ,
,
![]() =
между сечениями.
=
между сечениями.
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]() .
Определим поток вектора электрической
напряженности пронизывающи произвольную
замкнутую поверхность при условии, что
внутри этой поверхности находится не
один точечный заряд, а несколько зарядов.
Заряды могут иметь разные знаки.
.
Определим поток вектора электрической
напряженности пронизывающи произвольную
замкнутую поверхность при условии, что
внутри этой поверхности находится не
один точечный заряд, а несколько зарядов.
Заряды могут иметь разные знаки.
![]() ,
,
![]() .
.
Здесь
нужно знать определение: выходящая из
поверхности линия учитывается со знаком
«+», входящая со знаком «-». Общее число
пересечении всегда нечетное и
алгебраическая сумма пересечении равна
1. Из приведенного рассмотрения следует
важный вывод, который представляет
собой суть теоремы Ост.-Г.: поток линии
вектора электрической напряженности,
создаваемый точечными зарядами, через
произвольную замкнутую поверхность
равен:
![]() ,находящийся
внутри данной замкнутой поверхности.
,находящийся
внутри данной замкнутой поверхности.
Р ассмотрим
случай, когда мы имеем заряженное облако:
ассмотрим
случай, когда мы имеем заряженное облако:
 .
Введем понятие объемной плотности эл.
заряда–
.
Введем понятие объемной плотности эл.
заряда–
![]() .
.
![]() –
если заряд расположен равномерно,
–
если заряд расположен равномерно,
![]() –
не очень равномерно,
–
не очень равномерно,
![]() –
сильно не равномерно.
–
сильно не равномерно.
![]() ,
,
![]() .
.
![]() .
Теорема Остроградского_Гаусса
.
Теорема Остроградского_Гаусса
![]() .
По определению
.
По определению
![]()
![]() .
Ряд важных задач электростатики легко
решаются с помощью теоремы
Остроградского_Гаусса. В частности
задачи по определению напряженности в
данной точке ЭП. Особенно просто решаются
задачи в случае центральной, осевой или
плоскостной симметрии. Например: пусть
у нас имеется бесконечная плоскость
равномерно заряженная. Пусть положительным
зарядом с постоянной поверхностной
плотностью электрического заряда
.
Ряд важных задач электростатики легко
решаются с помощью теоремы
Остроградского_Гаусса. В частности
задачи по определению напряженности в
данной точке ЭП. Особенно просто решаются
задачи в случае центральной, осевой или
плоскостной симметрии. Например: пусть
у нас имеется бесконечная плоскость
равномерно заряженная. Пусть положительным
зарядом с постоянной поверхностной
плотностью электрического заряда
![]() .
.
![]() .
Задача. Определим напряженность в т.О.
Алгоритм:
.
Задача. Определим напряженность в т.О.
Алгоритм:
1. Выбери произвольную замкнутую поверхность проходящую через искомую точку и имеющую хорошую форму. 2. Запиши теорему Ост.-Г. 3. Запиши определение потока ФЕ.
![]()

![]() =[
=[
![]() ]=
]=![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]() .
.
4)
Электроемкость. Опыт
п оказывает,
что при увеличении заряда на проводнике
возрастает и его потенциал пропорционально
заряду, причем зависимость между φ и q
проводника оказываются прямопропорциональная.
оказывает,
что при увеличении заряда на проводнике
возрастает и его потенциал пропорционально
заряду, причем зависимость между φ и q
проводника оказываются прямопропорциональная.
![]() или
или
![]() ,
где С- коэффициент пропорциональности–электроемкость
или кратко- емкость, т.е.
,
где С- коэффициент пропорциональности–электроемкость
или кратко- емкость, т.е.
![]() =
=![]() (фарада).
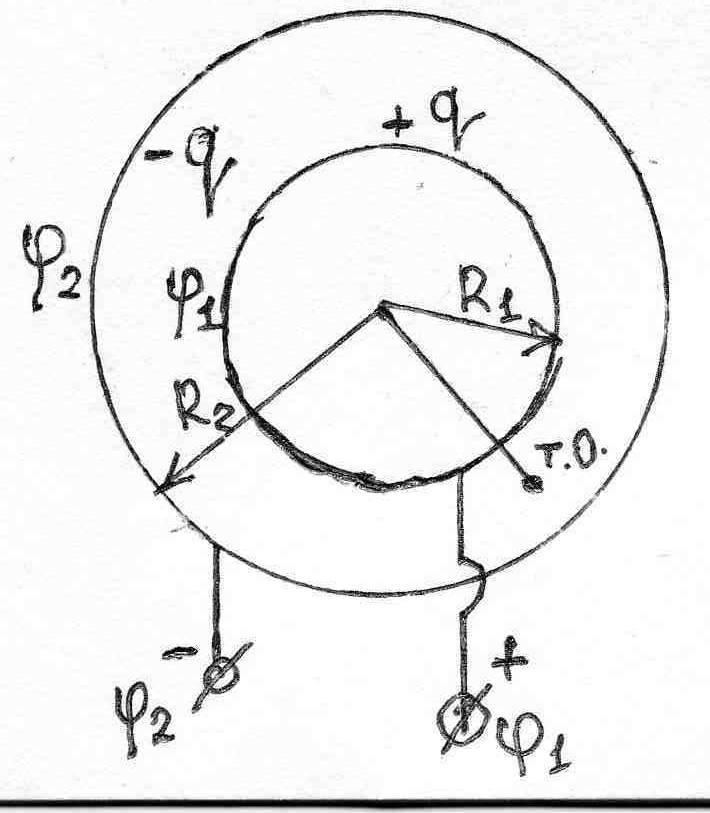
В случае шара радиуса R
и заряда q:
(фарада).
В случае шара радиуса R
и заряда q:
![]() .
На поверхности шара( проводника):
.
На поверхности шара( проводника):![]() ,
,
 ,
,![]() –емкость
шара радиуса R.
Емкость проводника не зависит от заряда
проводника и его потенциала, она
определяется размерами и формой
проводника, а также наличием вблизи
проводника других проводников.
–емкость
шара радиуса R.
Емкость проводника не зависит от заряда
проводника и его потенциала, она
определяется размерами и формой
проводника, а также наличием вблизи
проводника других проводников.
5)
Конденсаторы. Он
представляет собой систему из двух
проводников, которая имеет большую
электроемкость. Существуют различные
виды конденсаторов. а). плоский конденсатор.
![]() ,
,
![]() ,
,
 ,
,
![]() .
.
Если
пространство между пластинками заполнена
диэлектриком с диэлектрической
проницаемостью ξ, то емкость соответственно
возрастает в ξ раз, и формула для расчета
емкости принимает вид:
![]() .
При наличии диэлектрика во всех выражениях
электростатики вместо ξ0
входит ξξ0.
.
При наличии диэлектрика во всех выражениях
электростатики вместо ξ0
входит ξξ0.
б) сферически конденсатор.
![]() .
Также можно
написать и для φ1 и φ2.
.
Также можно
написать и для φ1 и φ2.
![]()

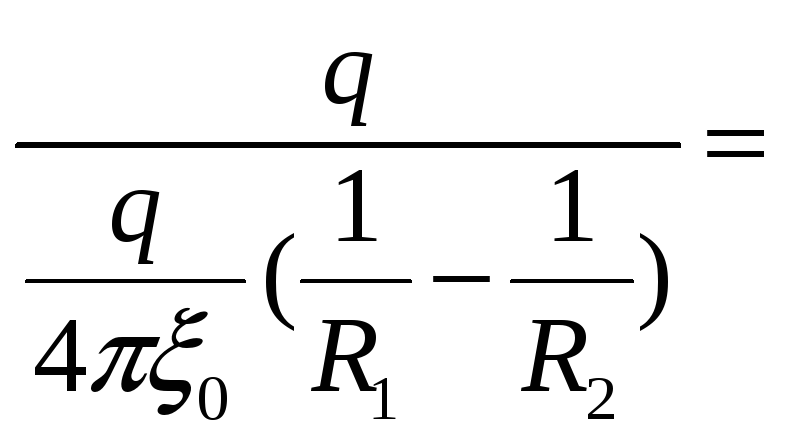
![]() –емкость
сферического конденсатора. В реальности
–емкость
сферического конденсатора. В реальности
![]() очень мало, поэтому
очень мало, поэтому
![]() ,
т.к.
,
т.к.
![]() .
.
в) цилиндрический конденсатор.
![]()
 ,
,
![]()

![]()
6 )
Энергия электростатического поля.
)
Энергия электростатического поля.
а).Энергия
системы точечных неподвижных зарядов.
![]() .
.
![]() –первое
начало термодинамики.
–первое
начало термодинамики.
![]() –т.к.
без теплообмена.
–т.к.
без теплообмена.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Можем
сформировать то же самое поле системы
2-х точечных электрических зарядов
иначе, полагая что +q2
находится в т.2, а 1-го заряда еще нет.
Пусть первый заряд находится на ∞, мы
будем перемещать его из ∞ в т. 1. Тогда
мы получим ту же самую систему с той же
самой энергией
![]() ,
,
![]() .
Можно сказать
.
Можно сказать
![]() ,
,
![]() ,
,
![]()
![]()
![]() .
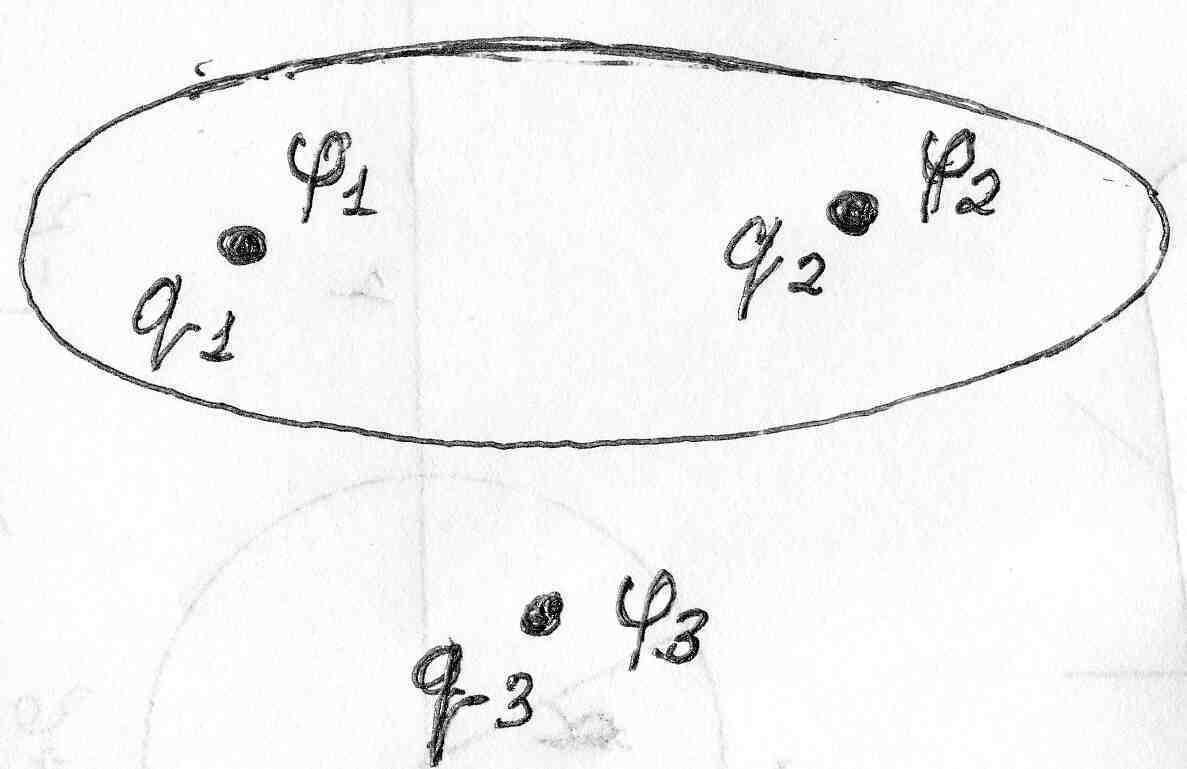
Добавим системе 3 точечный заряд
.
Добавим системе 3 точечный заряд
![]() .
Если много зарядов, то
.
Если много зарядов, то
![]() .(*)
.(*)
Вывод: энергия электростатического поля, состоящего из N зарядов, выражается формулой (*), где φi–потенциал, где находится данный i-ый заряд, создаваемый в этой точке всеми остальными зарядами, кроме данного i-го.
б)
Энергия заряженного проводника:![]()
![]() .
.
в)
Энергия заряженного конденсатора:
![]()
![]() –
для плоского конденсатора.
–
для плоского конденсатора.
7)
ЭП при наличии проводников. Рассмотрим
проводник. Поверхностная плотность в
разных местах будут различными. Исходя
из теоремы Остроградского-Гаусса можно
сказать, что напряженность ЭП в любой
точке внутри проводника равна нулю.
Исходя из соотношения между вектором
E
и вектором градиента (![]() ),
можно сказать, что φ внутри заряженного
проводника постоянна. Для дальнейших
соображении важно что φ в любой точке
одинаков, значит поверхность в любой
точке проводника является эквипотенциальной.
Значит линии напряженности входящие
или выходящие вблизи поверхности идут
перпендикулярно поверхности, т.к.
семейство линии напряженности
перпендикулярно к этой поверхности.
),
можно сказать, что φ внутри заряженного
проводника постоянна. Для дальнейших
соображении важно что φ в любой точке
одинаков, значит поверхность в любой
точке проводника является эквипотенциальной.
Значит линии напряженности входящие
или выходящие вблизи поверхности идут
перпендикулярно поверхности, т.к.
семейство линии напряженности
перпендикулярно к этой поверхности.![]() ,
,
![]() –определение.
–определение.
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
![]() .(*)
Из приведенного рассмотрения вытекает
следующие выводы: 1.Вне проводника: а)
поверхность проводника является
эквипотенциальной; б) вблизи поверхности
линии напряженности и вектор напряженности
перпендикулярно поверхности; в) вблизи
поверхности соответствует (*).
.(*)
Из приведенного рассмотрения вытекает
следующие выводы: 1.Вне проводника: а)
поверхность проводника является
эквипотенциальной; б) вблизи поверхности
линии напряженности и вектор напряженности
перпендикулярно поверхности; в) вблизи
поверхности соответствует (*).
2.Внутри
проводника: а)
![]() ;
б)
;
б)
![]() (
(![]() ).
Предположим, что заряженный проводник
имеет «-» заряд. Это значит, что он имеет
некоторое избыточное число электронов.
Они взаимодействуя по закону Кулона и
имея «-» заряд, отталкиваются и стремятся
разойтись как можно дальше. Т.к.
рассматриваем проводник, т.е. обладают
высокой проводимостью, т.е. электроны
легко перемещаются, то в результате
отталкивания расходятся друг от друга
и оказываются в тончайшем слое проводника,
причем большее скопление вблизи острия.
Поэтому поверхностная плотность
оказывается различной: на вогнутой
мала, на выпуклой – побольше, вблизи
заострении– очень большая:
).
Предположим, что заряженный проводник
имеет «-» заряд. Это значит, что он имеет
некоторое избыточное число электронов.
Они взаимодействуя по закону Кулона и
имея «-» заряд, отталкиваются и стремятся
разойтись как можно дальше. Т.к.
рассматриваем проводник, т.е. обладают
высокой проводимостью, т.е. электроны
легко перемещаются, то в результате
отталкивания расходятся друг от друга
и оказываются в тончайшем слое проводника,
причем большее скопление вблизи острия.
Поэтому поверхностная плотность
оказывается различной: на вогнутой
мала, на выпуклой – побольше, вблизи
заострении– очень большая:![]() .
Напряженность ЭП вблизи острия тоже
большая.
.
Напряженность ЭП вблизи острия тоже
большая.
8) Раскрыть методику изучения одного из элементов знания. Электромагнитное поле.
Формирование понятия электромагнитного поля в курсе физики средней школы начинают в базовом курсе, а завершают в старших классах профильной школы. В базовом курсе при введении элементарных сведений об электромагнитных явлениях, дают первоначальные представления об электрическом и магнитном полях, в старших классах - проводят количественное изучение электромагнитных явлений, рассматривают частные случаи электромагнитного поля, их свойства и характеристики, вводят понятие электромагнитного поля; при изучении электромагнитных волн вводят понятие свободного электромагнитного поля, знания об электромагнитном поле расширяют и обобщают при изучении волновой оптики и квантовой физики.
Обычно понятие электрического поля вводят при изучении электростатических явлений и связывают с покоящимися заряда-ми, а понятие магнитного поля вводят при изучении постоянного тока и связывают с током или движущимися зарядами. Понятие электромагнитного поля можно вводить в различных местах раздела «Электродинамика»: при изучении магнитного поля движущегося заряда, при изучении электромагнитных колебаний и волн. Программа общеобразовательной средней школы рекомендует ввести это понятие при изучении явления электромагнитной индукции.
Наиболее целесообразно вводить понятие электромагнитного поля в начале изучения раздела «Электродинамика».Начать изучение учебного материала целесообразно с развернутого введения в электродинамику, где на основе уже имеющихся у школьников знаний вводят первоначальные представления об электромагнитном поле. Дальнейшее изучение электромагнитных явлений углубляет и расширяет знания об электромагнитном поле. Обычно можно предъявить такие замечания по содержанию и возможную методику изучения материала введения в электродинамику, где вводят понятие электромагнитного поля. После повторения и обобщения основных сведений об электромагнитных явлениях, полученных учащимися в базовом курсе физики, выясняют особенности электродинамики, сравнивают ньютоновскую механику и электродинамику. Школьникам напоминают, что в механике они изучали силы тяготения, упругости и трения, которые зависят или от расстояния между взаимодействующими телами, или от их относительных скоростей. Затем предлагают пронаблюдать опыт по взаимодействию параллельных токов. Это типичный пример электромагнитного взаимодействия. Ребята наблюдают взаимодействие проводников, но не могут объяснить причину возникновения силы притяжения или отталкивания, так как расстояние d между проводниками и относительная скорость электронов в проводниках не изменяются. Значит, возникли силы, которых в механике не было, это силы электромагнитного взаимодействия. В этом случае говорят, что вокруг каждого из проводников возникло магнитное поле. Магнитное поле одного проводника действует на другой проводник с током с некоторой силой. Правомерно говорить и наоборот: магнитное поле второго проводника действует на первый.
Затем излагают вопрос о передаче взаимодействий. Ньютоновская механика опирается на принцип дальнодействия (взаимодействия передаются мгновенно на сколь угодно большие расстояния). По существу, учащиеся это знают, но данную сторону вопроса теперь следует подчеркнуть и оттенить. Отличительная особенность электродинамики - необходимость трактовки электромагнитных явлений с позиций другой концепции (концепции близкодействия), согласно которой взаимодействия между зарядами (токами, магнитами) передаются с конечной скоростью.
Далее школьникам сообщают, что конечность скорости передачи взаимодействий приводит к тому, что если заряд из точки А переместится в некоторую точку А'', то изменение силы, действующей на заряд в точке В, произойдет не мгновенно, а спустя некоторое время. Поскольку взаимодействие между электрическими зарядами распространяется с конечной скоростью (и в среде, и в пустоте), то имеет место какой-то процесс, распространение которого происходит с конечной скоростью. Тогда должен быть и какой-то материальный объект, с которым этот процесс происходит, так как нельзя представить себе процесс, который бы осуществлялся при отсутствии чего бы то ни было реально существующего. Все это можно объяснить, только введя понятие об электромагнитном поле. Реальность электромагнитного поля подтверждается и иллюстрируется хорошо известными учащимся фактами: распространением электромагнитных волн (радиосвязь, телевидение). Эффектны примеры с радиолокацией Луны, с управлением луноходом и др.
