GOS / 16 Дифракция света

16.Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля и Фраунгофера. Дифракционная решетка. Дифракция рентгеновских лучей.

Дифракция световых волн заключается в огибании волнами преград, препятствий разной формы и попадания волн в область тени. Эффект дифракции волн ярко выражен когда

размеры препятствий превосходя длину волны оказываются

соизмеримыми с длиной волны.Однако явление дифракции света

наблюдается и от крупных объектов, но в этом случае необходимо

удалять экран наблюдения на большие расстояния.

В лабораторных условиях дифракция осуществляется на базисе порядка 1м,

и резко выраженный эффект обнаруживается при размерах преград d=1мм или меньше.

Явление дифракция света качественно можно представить исходя из принципа Гюйгенса (к-ц 17в)

Принцип Гюйгенса Пусть мы имеем источник света. Каждая точка фронта волны представляет собой

элем-й источник вторичных волн. Фронт волны в следующий момент времени дает огибающую вторичных волн.

Принцип Гюйгенса-Френеля: каждая точка фронта волны является элементарным источником вторичных волн, интерференция вторичных волн и определяет освещенность в заданной точке экрана наблюдения.

Однако принцип Гюйгенса не позволяет определить интенсивность света, идущего от преграды в данном направлении, поэтому решение задачи на дифракцию света носит только качественный характер. Френель дополнил принцип Гюйгенса принципом интерференции света.

Выразим освещенность в данной точке экрана наблюдения исходя из принципа Г-Ф для свободного фронта волны.

Запишем амплитуду элементарного воздействия на т.О: (1)

- амплитуда колеб., исходящего от поверхности фронта волны площадью 1м²

- амплитуда колебания, исходящего от элементарного участка фронта волны площадью

Запишем само колебание: _(1а)

Для определения величины воздействия всего фронта волны в данной точке надо учесть интерференцию вторичных волн по Френелю, иначе говоря надо проинтегрировать последнюю ф-лу по всей поверхности (2)

Расчёт по формуле (2) обычно предсиавляет собой трудную задачу. Френель разработал в двльнейшем метод который получивший название метода зон Френеля., который позволяет сравнительно просто в ряде задач опред. освещенность не прибегая к сложному интегрированию.Суть метода заключается в том, что поверхность фронта волны делится не на бесконечно малые

Д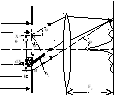ифракция в сходящихся лучах (дифракция Френеля)

Рассмотрим расположение в котором имеется точечный источник света, экран наблюдения и между ними расположен объект дифракции в виде прозрачного

экрана с дыркой. Воспользуемся методом зон Френеля.

Воспользуемся принципом Гюйгенса-Френеля.

В т.О – эффект дифракции в сходящихся лучах.

Дифракция в параллельных лучах (Дифракция Фраунгофера)

Фраунгофер(нем.,1-я полов. 19в.)

После прохождения объекта дифракции лучи

идут параллельно

. Физический смысл принципа Гюйгенса-Френеля. Вывод на его основе законов геометрической оптики.

По Гюйгенсу свет представляет собой волну. (Формулировка принципа Гюйгенса)

Вывод на его основе закона преломления

Задачи по дифракции в //-х лучах

Задача состоит в расчёте распределения освещенности

дифракционной картины в плоскости экрана Э( в фокальной

плоскости линзы Л). В соответствии с принципом Г-Ф

необходимо рассчитать результат интерференции лучей от всех

элементарных полосок dX от X=0 до X=b приходящих в

произвольную т.О. Интерф. предс. собой суммирование

всех таких элементарных воздействий с учётом фазовых соотношений. При расчете будем

учитывать, что разность фаз, приходящих колебаний

в т.О определяется разностью хода колебаний различных элементов, а разность хода легко

выражается через угол дифракции ψ. От плоскости АС перпендикулярной к пучку

диффрагированных лучей, лучи от разных мест до т.О проходят различный геометрический путь,

но один и тот же оптический путь. Т.о. разность хода определяется различием расстояния от

плоскости щели до плоскости АС.

-амплитуда колебания, исходящего от всей ширины щели,

- амплитуда колебания, исходящего щели, единичной ширины.

- амплитуда колебания, исходящего от бесконечно малой ширины щели (dx)

-элементарное колебание, приходящее в т.О от элемента dx

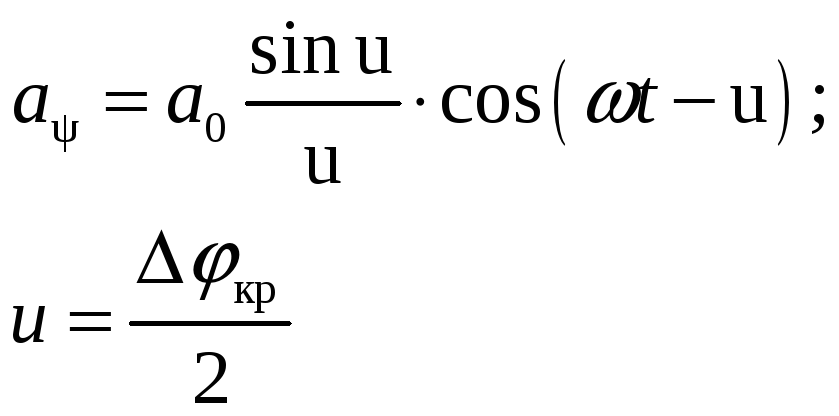. (7)

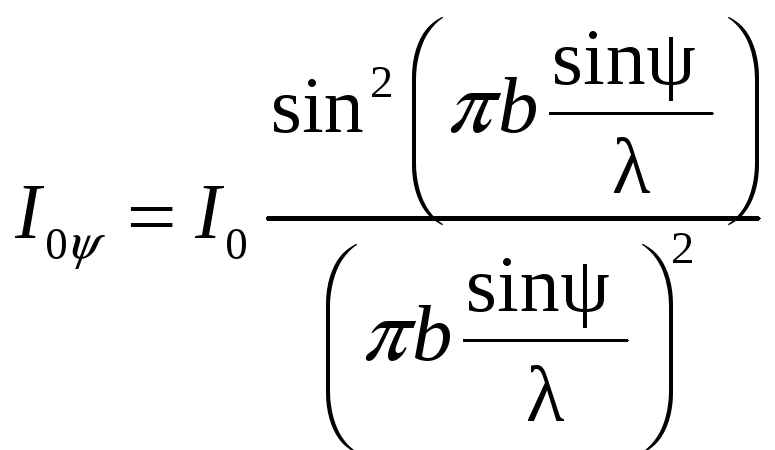Интенсивность светового пучка и освещённость в т.О или энергия приносимая в эту точку пропорциональна квадрату амплитуды: (8) (8а),

Изобразим распределение (8) и (8а) графически:

Как следует из расчёта распределение освещенности на экране

Э представляет собой главный максимум большей освещенности

И систему прилегающих к нему слабых вторичных

максимумов разделённых минимумом нулевой освещенности.

Сформулируем условие минимумов и вторичных максимумов. Чтобы образовался минимум

необходимо чтобы числитель в формулах (7) и (8) обратился в ноль, при условии что знаменатель не равен нулю.

Если:-минимум нулевой освещенности, то числитель равен нулю при этом знаменатель не равен 0, (9)- минимум k=1, 2, 3,…

Если: -вторичные максимумы, то числитель (8) равен 1 (10)-вторичные максимумы k=1, 2, 3,… Во вторичных максимумах

Формула (11)

Все результаты можно подтвердить исходя из метода векторных диаграмм, которые в ряде задач являются плодотворными.

Дифракционная решетка

Дифракционная решетка представляет собой совершено высококачественный современный спектральный прибор. Характеристики дифракционной решетки:

- свободная область дисперсии, -спектральный предел разрешения, R-спектральная разрешающая сила,-светосила прибора,-

угловая дисперсия.

Теорию дифр. решетки рассмотрим используя метод индукции. В рассуждениях будем увеличивать число щелей решетки и наблюдать влияние такого увел-я на распр-е освещенности. Кроме прозрачных решеток нанесенных на пластинах стекла или плавленого кварца широко используют отражательные решетки, штрихи которых наносят на пов-ть металлич. зеркала, плоского или выпуклого. Выпук. отраж-е решетки исполь-т без применения стеклянных или кварцевых линз. это позволяет проводить спектр-е исслед-я в далеких УФ области спектра, для которых даже воздух оказ-ся сильно поглощающей средой.

Расс-м случай дифр. от 2-х одинаковых щелей.

Пусть: b- ширина каждой щели, с- расстояние между щелями.м

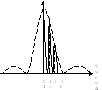
∆φ_сосед=0 a_рез=2а₀; I=4I₀

т. 1: ∆φ_сосед=π a_рез=0; I=0;

т.2:φ_сосед=2π a_рез=2а₂; I=4I₂;

т.3.∆φ_сосед=3π a_рез=0; I=0;

т. 4: ∆φ_сосед=4π a_рез=2a₄ I=4I₄;

аналогичным образом рассматривается, когда число щелей возрастает.1)по мере увеличения числа щелей в решетке поисходит сужение главных максимумов. Ширина главного максимума оказывается пропорциональной 1/N, N – число щелей. 2) Интенсивность глав. максимумов возрастает пропорционально N².3) Между соседними главными максимумами появляются вторичные максимумы и минимумы, число втор. макс.=N-2 и N-1 – минимумов. На практике используют решетки, в которых число щелей составляет 10 000 и даже 100 000, поэтому реальная оптическая решетка формирует систему очень узких ширина пропорциональной 1/N и очень сильный главный максимум, а вторичные максимумы создают только слабый фон.Запишем усл. главного максимума для реальной решетки:

(12)-усл. глав. max от решетки

(13)Среди мн-ва min от решетки особый интерес пред-т 1-й минимум прилегающий главн. данному максимуму. (16) где k=0,1,2,..; m=1,2,…N-1.Ф-ла(16) дает усл. минимумов от решетки. Учитывая (17)-усл. миним-в от решетки

Основ. св-во дифр. решетки сост. в перераспределении первич. пучка в некотор. избранных стого определенных напрвлений удов-х усл. глав. max (14)

решетка представляет собой переизлучатель света. Расчет приводит к функции распределения интенсивности : (18), где I₀-интенсивность от решетки под углом ψ=0

- половина сдвига фаз от краев одной щели

- половина сдвига фаз от соседних лучей

(18), где I₀ – интенсивность от решетки под углом ψ=0

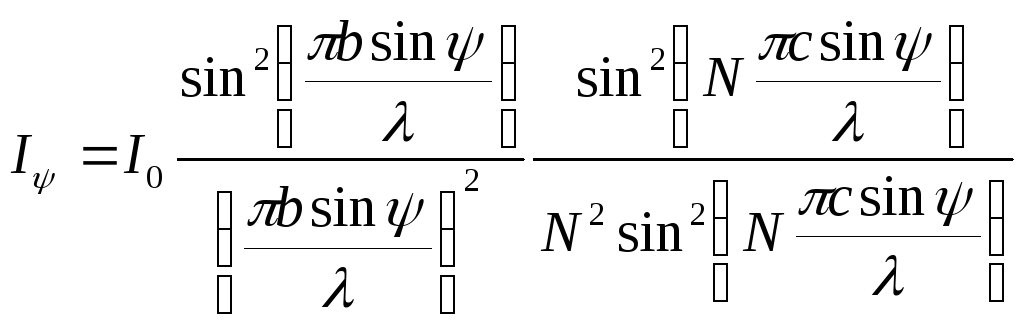
1-ая тригонаметрическая формула (18) учитывает влияние дифракции от одной щели, 2-ая учитывает влияние N-лучевой интерференции. В главных максимумах 2-ая тригонаметрическая ф-ция в(18а) принимает максимальное значение равное 1. В ф-ле (18б) 2-ая тригонаметр. ф-я в главных максимумах принимает значение N² и м/у I₀ и I₀₁ имеет соотношение : ,нетрудно доказать, что макс. значение 2-й триг. ф-ии, т.е. ее значение в области главных максимумов : (14)

Нулевое значение 2-й тригонаметрической ф-ии соотв-т условию (17) – минимумы (нули),k=0,1,2…., m=1,2,3,…, N-1

Основной ф-ой теории дифр решетки является условие главных максимумов (14). Важным соотношением теории дифр решетки является условие минимумов (17). Нетрудно видеть, что подстановка (14) в ф-лу (18а) приводит к тому, что 2-й трин. сомножитель опред. в неопределенность (0/0). Если эту неопределенность раскрыть по Лопиталю, то увидим что это соотношение принимает максимальное значение равное 1. Т.о. ф-ла (14) – условие макс. нах-ся в полном соответствии с распределением (18а). Аналогично подстановка (17) минимумов(нулей) в (18а) приводит к тому ,что числитель тригонаметрического сомножителя обращается в ноль , тогда как знаменатель оказывается отличным от нуля, т.е. соотношение (17) обращает 2-й триг. сомножитель в нуль. Ф-ла (17) находится в полном

соответствии с (18а ). Применение дифр. реш. – мощный спектральный прибор, предназначенный для измерений.

“Наблюдение дифракции света на узкой щели”

Оборудование: (см рисунок№ 9)

1. Сдвигаем ползунок штангенциркуля до образования между губками щели шириной 0,5 мм.

2. Приставляем скошенную часть губок вплотную к глазу (располагая шель вертикально).

3. Сквозь эту щель смотрим на вертикально расположенную нить горящей лампы.

4. Наблюдаютем по обе стороны от нити параллельные ей радужные полоски.

5. Изменяем ширину щели в пределах 0,05 – 0,8 мм. При переходе к более узким щелям полосы раздвигаются , становятся шире и образуют различимые спектры. При наблюдении через самую широкую щель полосы очень узки и располагаются близко одна к другой.[9]

6. Ученики зарисовывают в тетрадь увиденную картину.

Экспериментальная работа № 5.

“Наблюдение дифракции света на капроновой ткани”.

Оборудование: лампа с прямой нитью накала, ткань капроновая размером 100x100мм (рисунок 10)

1. Смотрим через капроновую ткань на нить горящей лампы.

2. Наблюдаем “дифракционный крест” (картина в виде двух скрещенных под прямым углом дифракционных полос) . [9]

3. Ученики зарисовывают в тетрадь увиденную картину (дифракционный крест ).

Объяснение: В центре краста виден дифракционный максимум белого цвета. При k=0 разность хода волн равна нулю, поэтому центральный максимум получается белого цвета.

Крест получается потому, что нити ткани представляют собой две сложенные вместе дифракционные решетки со взаимно перпендикулярными щелями. Появление спектральных цветов объясняется тем, что белый свет состоит из волн различной длины. Дифракционный максимум света для различных волн получается в различных местах. [9]

Экспериментальная работа № 6.

“Наблюдение дифракции света на грампластинке и лазерном диске”.

Оборудование: лампа с прямой нитью накала, грампластинка (см. рисунок 11)

Грампластинка является хорошей дифракционной решеткой.

1. Располагаем грампластинку так, чтобы бороздки расположились параллельно нити лампы и наблюдаем дифракцию в отраженном свете.

2. Наблюдаем яркие дифракционные спектры нескольких порядков.

Объяснение: Яркость дифракционных спектров зависит от частоты нанесенных на грампластинку бороздок и от величины угла падения лучей. (см. рисунок 12)

Почти параллельные лучи, падающие от нити лампы, отражаются от соседних выпуклостей между бороздками в точках А и В. Лучи, отраженные под углом равным углу падения, образуют изображение нити лампы в виде белой линии. Лучи, отраженные под иными углами имеют некоторую разность хода, вследствие чего происходит сложение волн.

Аналогичным образом пронаблюдаем дифракцию на лазерном диске. (см. рисунок 13)

Поверхность компакт-диска представляет собой спиральную дорожку с шагом соизмеримым с длиной волны видимого света.На мелкоструктурной поверхности проявляются дифракционные и интерференционные явления. Блики компакт- дисков имеют радужную окраску.

Дифракция волн на воде

Методы исследования в науке — это система приемов и процедур деятельности, направленной на выполнение определенной исследовательской задачи. Всякая наука использует наряду с общенаучными специфические методы исследования. Для достижения цели в конкретном исследовании применяется система методов, правильный выбор которых оптимизирует исследование и повышает его результативность. Теоретические методы психолого-педагогического исследования опосредованно и непосредственно выходят на анализ реальных образовательных процессов (их причин, источников развития, системы условий, обеспечивающих их эффективное функционирование). Эмпирические методы направлены на диагностику и изменение состояния исследуемого объекта.  Методы количественного и качественного анализа позволяют систематизировать полученную при использовании эмпирических методов информацию и сделать предварительные выводы о наличии причинно-следственных связей между явлениями.  В сфере гуманитарного познания, к которой относится педагогика, все большее распространение получают качественные методы исследования, предшествующие выбору и применению математических и статистических методов. Они помогают избежать односторонности в получении научного знания, нивелирования индивидуальности воспитанников, а также обеспечить целостное восприятие их различий как объективный факт и норму. Соблюдение баланса между количественным и качественным в конкретном исследовании позволяет достичь подлинной научности. При качественном анализе человек представляет для исследователя интерес не только как объект изучения и источник информации, но и как особый мир образов и переживаний. В. В. Краевский выделяет некоторые наиболее характерные особенности качественных методов исследования: - инструменты измерения разрабатываются и проверяются в ходе самой научной работы, часто являются специфическими, отражают индивидуальный исследовательский подход; - исследовательские процедуры на качественном уровне дублируются редко; - анализ осуществляется путем обобщения идей из собранных эмпирических данных; организация данных направлена на получение целостной картины. Психологическая и педагогическая науки предназначены для выявления закономерностей образовательного процесса как объективных оснований педагогической деятельности. Выбор методов конкретного исследования — задача исследователя, способы решения которой рассматриваются в след. лекциях..  2.5. Закономерности как предмет научного исследования. Всякая наука исследует определенный класс закономерностей, объективно существующих в выбранной области действительности. Знание о закономерностях позволяет моделировать происходящие в данной области процессы, прогнозировать их и проектировать эффективную (продуктивную) деятельность. При этом под закономерностями понимаются устойчиво повторяющиеся причинно-следственные связи между явлениями. Многие педагоги считают себя «специалистами» в области психологии: они ведь общаются, решают учебно-воспитательные задачи, «понимают» друг друга и т.п. На самом деле речь идет о так называемой «житейской психологии», которая имеет полное право на существование. Многие психологи-профессионалы опираются на опыт житейской психологии, включая и свой собственный жизненный опыт. Но в психолого-педагогических исследованиях все-таки необходимо различать научную психологию и психологию житейскую. Ю. Б. Гиппенрейтер выделяет следующие различия. 1. Житейские знания конкретны, связаны с конкретными жизненными ситуациями, а научная психология стремится к обобщенному знанию, основанному на выделении общих закономерностей жизни и поведения людей. 2. Житейские знания носят больше интуитивный характер, а в психологической науке стремятся к рациональному объяснению психических явлений, т.е. к лучшему их пониманию и даже прогнозированию. 3. ^ Житейские знания передаются в очень ограниченных вариантах (из уст в уста, через письма и т.п.), а научные знания передаются через ‑­ специальную систему фиксации накопленного человеком опыта (через книги, лекции, аккумулируются в научных школах и т.п.). 4. В житейской психологии получение знаний осуществляется через наблюдения, рассуждения или через непосредстведное переживание человеком тех или иных событий. В научной психологии новые знания получаются в специальных исследованиях и экспериментах, а также в особых формах научного мышления и воображения («воображаемый эксперимент»). 5. ^ Научная психология располагает обширным, разнообразным и уникальным фактическим материалом, недоступным ни одному носителю житейской психологии. Особая характеристика научного знания — его системность и упорядоченность, что позволяет каждому психологу-профессионалу ориентироваться во всем многообразии этого знания. ^ Но при этом нельзя говорить, что научная психология непременно «лучше» житейской, так как на самом деле они взаимодополняют друг друга'. В психологии поиск общих закономерностей отличается обобщенностью полученной научной информации. Психологические особенности отдельного индивида представляют ценность как факт для обобщенных выводов о закономерностях возрастной психологии, педагогической психологии, психологии личности и индивидуальных различий, социальной психологии. В образовательной деятельности довольно часто выделяются следующие общие психологические закономерности: - обучение ведет за собой развитие; - развитие связано со становлением натуральных и высших психических функций (логическое запоминание, целенаправленное мышление, творческое воображение, произвольность психических процессов); - расширение зоны актуального состояния знаний и умений ребенка задается компетентным взрослым (педагогом и родителем) через зону ближайшего развития; - учет возрастных психологических особенностей учащихся осуществляется через понимание педагогом состояния социальной ситуации развития ребенка, возможностей становленияведущей деятельности, возрастных психологических новообразований; - учебная деятельность формируется на основе завершенности развития ведущей деятельности на предыдущем возрастном этапе (игровая деятельность), а ее эффективное освоение закладывает основу для разворачивания последующей (деятельность общения); - основа эффективности овладения обучающимся учебной деятельностью — это учебная задача, которая решается через поэтапное формирование умственных действий; - эффективное взаимодействие в деятельности общения педагога и обучающегося предполагает необходимость построения соответствующих взаимоотношений, определяющих возможности взаимовлияния и взаимопонимания. В педагогике выявлен и сформулирован ряд общих закономерных связей, существующих в педагогической деятельности. В. В. Краевский выделяет следующие из них: - освоение подрастающими поколениями социального опыта старших поколений (к нему обращаются всякий раз, когда речь идет о педагогической науке и ее объекте); - социальная сущность образования, обусловленность всех его элементов социально-экономическим состоянием общества; - взаимодействие учителя и ученика, воспитателя и воспитанника в образовательном процессе, без которого нет самого этого процесса; - единство содержательной и процессуальной сторон обучения. В педагогике закономерности действуют так же неотвратимо, как и в природе. И они носят такой же объективный характер, т.е. не зависят от воли конкретных людей. Однако так же, как и законы природы, педагогические закономерности не фатальны: их учет не означает подчинения. Для примера вспомним о неотвратимости действия закона всемирного тяготения. Его можно не знать или презирать, но, споткнувшись, упадешь вниз. Однако именно на понимании этого закона были разработаны летательные аппараты. Понимание законов гидро- и аэродинамики позволило мореходам ходить на паруснике против ветра, галсами.  Так же и понимание педагогических закономерностей позволяет оптимизировать деятельность учителя, воспитателя, руководителя школы. Нередко можно услышать, что «воспитывает жизнь, она все расставляет по своим местам; и если воспитание противоречит окружающей жизни, оно безрезультатно — жизнь всегда побеждает». Но ведь известно, что, к примеру в одной и той же семье (т. е. в одних и тех же обстоятельствах, «в одной и той же жизни») вырастают совершенно разные дети. Освоение опыта не происходит пассивно, путем подчинения традиции, оно протекает в ‑­ осмыслении этого опыта, в выработке собственного отношения к нему, во взаимодействии взрослого и ребенка, педагога и воспитанника. Если помочь воспитаннику выработать конструктивную позицию, то можно помочь ему стать успешным даже во враждебном окружении.