
GOS / 3 Законы сохранения
.doc3. 24.Раскрыть содержание понятий. Импульс и момент импульса. Законы сохранения импульса. Законы сохранения момента импульса. Кинетическая и потенциальная энергия. Закон сохранения механической энергии. Потенциальные силовые поля и их свойства. Охарактеризовать этапы введения понятия «механическая работа». Раскрыть методику изучения закона сохранения импульса и дать примеры задач на ее усвоение. Сформулировать затруднения уч-ся при формировании понятия «потенциальная энергия» и пути их преодоления.
Второй
з-н Ньютона можно записать в виде:
 ;
;
![]() ,
где
,
где
![]() - вектор импульса тела.
- вектор импульса тела.
Р ассм-им
систему матер. точек. Силы, действующие
между точками этой сис-мы назовем
внутренними.
ассм-им
систему матер. точек. Силы, действующие
между точками этой сис-мы назовем
внутренними.
О бозначим
внутренние силы:
бозначим
внутренние силы:
![]() - внутренняя суммарная сила, действующая
на данную точку со стороны др. точек,
принадлежащих рассм-ой сис-ме.
- внутренняя суммарная сила, действующая
на данную точку со стороны др. точек,
принадлежащих рассм-ой сис-ме.
![]()
![]() -
внешняя суммарная сила.
-
внешняя суммарная сила.
По отношению к каждой из матер. точек можно применить 2 закон Ньтона, и записать т.о. n Ур-ий, где n-число матер. точек.
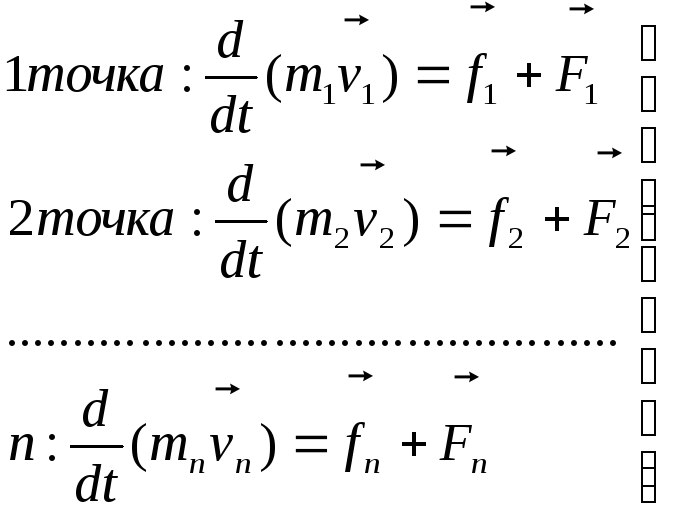 n
– уравнений, где n-число
матер. точек.
n
– уравнений, где n-число
матер. точек.
Просуммируем
эту систему:
 .
Т.к.
.
Т.к.
![]() ,
то
,
то
![]() ;
(1)
;
(1)
Сумма всех внутренних сил оказ-ся равной нулю, поскольку в эту сис-му войдет множ-во парных сил равных по величине и противоположных по напр-ию.
Расс-им некот-ую совок-ть тел. Это может быть напр-р ж/д состав, сис-ма планет. Выделим какую-нибудь часть тел.
Тела
наход-ся внутри этой сис-мы назовем
внутренними,
а силы, которые дейст-ют на каждое тело
внутри сис-мы – внутренними.
![]() -суммарная
внутр-я сила.
-суммарная
внутр-я сила.
Тела
нах-ся вне системы – внешние.
![]() -суммарная
сила, действующая на i-ое
тело со стороны др. внешних тел.
-суммарная
сила, действующая на i-ое
тело со стороны др. внешних тел.
Пример.

 ;
;
![]() ,
,
![]() ;
Просуммируем
;
Просуммируем
![]() .
.
![]() (2).
(2).
З амкнутая
сис-ма. Под
замкнутой (изолированной) сис-мы тел
подразумевают такую сис-му, на которую
не действуют внешние тела, или действие
внешних сил компенсировано.
амкнутая
сис-ма. Под
замкнутой (изолированной) сис-мы тел
подразумевают такую сис-му, на которую
не действуют внешние тела, или действие
внешних сил компенсировано.
В
этом случае:
![]() (по опр-ю замкн. сис-мы).
(по опр-ю замкн. сис-мы).
![]() (3) – для замкнутой сис-мы. Следовательно
(3) – для замкнутой сис-мы. Следовательно
![]() (4)
(4)
Соотн-ие
(4) выражает фундаментальрый з-н мех-ки
сис-мы матер. точек: суммарный
импульс в замкнутой сис-ме остается не
изменным при всевозможных процессах,
происходящих в этой замкн. сис-ме.
![]() (4а)
(4а)
Рассмотрим момент импульса. При движении тела (матер. точек) по криволин-й траектории действия на это тело со стороны другого или других тел зависит не только от величины этой силы, но и от его направления и места его приложения. Все характеристики криволинейного движ-ия зависит в значительной степени и от радиус-вектора. Модуль которого представляет собой расстояние от матер. точки до центра.
![]() (5),
(5),
![]() -
вектор момента импульса.
-
вектор момента импульса.
![]() -
радиус-вектор.
-
радиус-вектор.
![]() -
импульс
-
импульс
![]() ;
;
![]() (6)
(6)
Вектор
момента импульса
![]() напр-ен перпендикулярно плоскости в
направлении в шпаргалку.
напр-ен перпендикулярно плоскости в
направлении в шпаргалку.
![]() ,
,
![]() (6а)
(6а)
![]() -момент
силы;
-момент
силы;
![]() -вектор
момента силы.
-вектор
момента силы.
![]() (7)
(7)
![]() (7а)
(7а)
![]() (7б)
(7б)
![]() (7в),
где
(7в),
где
![]() -плечо силы.
-плечо силы.
![]() (8г).
(8г).
![]() -
вектор момента импульса.
-
вектор момента импульса.![]() .
.
Рассмотрим
сис-мы тел, выделим внутренние и внешние
части:
 ;
;
![]() -
для единст. матер. точки.
-
для единст. матер. точки.
Запишем
данное соот-ие для каждого внутреннего
тела:
![]() ;,
где
;,
где![]() - суммарный момент внешних сил, действующих
на i-е
внутренне тело;
- суммарный момент внешних сил, действующих
на i-е
внутренне тело;
![]() - суммарный момент внутренних сил,
действующих на i-е
внутренне тело.
- суммарный момент внутренних сил,
действующих на i-е
внутренне тело.
Просуммируем:
![]() (9).
(9).
![]() ,
где
,
где
![]() -
плечо силы. Т.к.
-
плечо силы. Т.к.
![]() ,
то следовательно
,
то следовательно
![]()
 .
.
![]() (10)
(10)
Для
замкнутой сис-мы, по определению суммарный
момент внешних сил
![]() .
Следовательно:
.
Следовательно:
![]() (11)
(11)
![]()
![]() .
(12)
.
(12)
В замкнутой сис-ме тел (матер. точек) суммарный момент импульса остается не изменным при всех процессах, происходящих в этой замкнутой сис-ме тел.
Этот фундаментальный закон замкнутой сис-мы матер. точек носит название закона сохранения момента импульса.
Кинетическая энергия.
Выразим
кинетическую энергию тела через работу:

Док-во:
![]() ;
;
![]() ,
,
![]() ;
;


![]() (13);
(13);
![]() (14), где
(14), где
![]() -
кинетическая энергия матер. точки.
-
кинетическая энергия матер. точки.
![]() (15)
(15)
Матер. точка движ-ся испытывая воздействие окружающих тел двух типов. Во-первых, при непоср-ом контакте с окр-ми телами, во-вторых под воздействием внешних силовых полей.
Различные силовые поля обладают различными свойствами. Можно выделить особую группу силовых полей, которую называют потенциальными полями, а силы действующие в потенциальных полях называют потенциальными или консервативными силами.
О сновное
свойство потенйиальных полей состоит
в том, что работа по перемещению тела
из одной точки пространства в другую
не зависит от пути перемещения:
сновное
свойство потенйиальных полей состоит
в том, что работа по перемещению тела
из одной точки пространства в другую
не зависит от пути перемещения:
![]() (16)
(16)
К числу потенциальных полей относятся гравитационные поля, силовое взаимодействие в котором подчиняется з-у всемирного тяготения, и электростатические поля, взаимодействия в которых подчиняется з-у кулона.
Из соот-ия (16) следует вывод, что в потенциальном поле работа по замкнутому пути, в котором тело возвращается в исходную точку равно нулю.
 ;
;
![]() (16а).
(16а).
Потенциальная энергия.
Важной характеристикой потенциального поля является потенциальная энергия.
![]() (17),
(17),
где
![]() - потенциальная энергия матер.точки в
потенциальном силовом поле в точке 1.;
- потенциальная энергия матер.точки в
потенциальном силовом поле в точке 1.;
![]() - потенциальная энергия матер.точки в
потенциальном силовом поле в точке 0.
- потенциальная энергия матер.точки в
потенциальном силовом поле в точке 0.
Соот-ие
(17) опред-т вел-ну потенц. энергии в
произвольной точке 1. Связывая ее с
потенц. энергией в некоторой точке0,
которую условно принимают за начальную
вел-ну. По соот-ию (17), потенц. энергия в
данноц произвольной точке оказ-ся
известной с точностью до аддитивной
постоянной
![]() .
.
Р ассмотрим
потенциальное силовое поле.
ассмотрим
потенциальное силовое поле.
![]() ;
;
![]()
![]() ;
;
![]() ,
а т.к.
,
а т.к.
![]() ,
то ,
,
то ,
![]() ,
,
![]()
![]() (18)
(18)
Формула (18) выражает важный закон мех-ки: в потенциалбном поле, в котором действуют консервативные, суммарная мех-ая энергия, которая предст-ет сумму потенциальной и кинетической энергий остается не изменой при любых перемещениях. Этот з-н сохр-я полной мех-й энергии справедлив только в потенц-х силовых полях, только при действии консервативных сил.
Если тело испытывает воздействие непотенциальных или неконсервативных сил, то з-н сохр-я полной мех-й энергии места не имеет; при движении под действием непотенциальных или неконсервативных силполная мех-я энергия не сохр-ся.
Примером непотенциальных сил яв-ся силы трения. Если надвиж-ия тела, кроме потенциальных сил действуют еще и силы трения и другие непотенциальные силы, то суммарная мех-ая энергия не яв-ся постоянной, и все время изменяется.
![]() ;
;
![]() ;
;
![]() .
Продифференцируем последнее.
.
Продифференцируем последнее.
![]()
 ;
;
![]() ;
;![]()
![]() .
.
Р ассм-м
движ-е в прямоуг-й декартовой сис-е
координат. Предположим, что при этом
движении изменяеися только координата
x,
т.е. пусть движение происходит под
действием силы, параллельной вдоль оси
OX.
Тогда
ассм-м
движ-е в прямоуг-й декартовой сис-е
координат. Предположим, что при этом
движении изменяеися только координата
x,
т.е. пусть движение происходит под
действием силы, параллельной вдоль оси
OX.
Тогда
![]() ;
;
 -
частная производная П по X.
Аналогично находятся частные производные
по y
и z.
-
частная производная П по X.
Аналогично находятся частные производные
по y
и z. (19).
(19).
Общий
случай
![]() .
.
![]()
![]() -
градиент.
-
градиент.
Градиент
скалярной функциипредставляет
вектор, численно равный быстроте
изменения данной функции в направлении
наибыстрейшего его изменеия и направленный
в этом направлении. .
.
![]() ,
,
![]() -
оператор Гамильтона.
-
оператор Гамильтона.
![]() (20);
(20);
![]() (20а);
(20а);
![]() (20в).
(20в).
Раскрыть методику изучения закона сохранения импульса и дать примеры задач на ее усвоение. При изучении закона сохранения импульса вводят ряд новых физических понятий. Усвоение некоторых из них очень важно для изучения всего раздела. К числу этих понятий следует отнести такие: механическая система, замкнутая механическая система, внешние силы, внутренние силы, консервативные силы.
Понятие «замкнутая механическая система» является идеализацией. Очень важно поэтому при рассмотрении конкретных задач оговаривать, как движутся тела физической системы и действуют ли на них внешние силы. Если эти силы отсутствуют (т. е. ими можно пренебречь), то нужно применять закон сохранения импульса; если внешние силы действуют, то суммарный импульс силы, действующий на систему, равен суммарному изменению импульса системы.
Для простоты рассуждений рассмотрение закона сохранения импульса целесообразно начинать для замкнутой системы, состоящей из двух сталкивающихся тел, массы которых одинаковы, а скорости различны. Выводят этот закон на основе второго и третьего законов динамики, что вполне логично.
Доказывают, что изменение импульсов этих двух сталкивающихся тел одинаково по модулю, но противоположно по знаку.
Далее формулируют закон: геометрическая сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Суммарный импульс только перераспределяется между взаимодействующими телами системы. Закон обязательно должен быть проиллюстрирован экспериментом и примерами. Могут быть показаны следующие опыты: с взаимодействующими тележками, поставленными на рельсы, с маятником, с заводной игрушкой и картонной платформой, поставленной на параллельные друг другу одинакового размера ролики.
Первые задачи целесообразно решить графически, с тем чтобы учащиеся уяснили, что в законе речь идет о геометрической (векторной) сумме импульсов. Остановимся на одном из примеров такого типа: «Радиоактивное ядро до распада обладало некоторой скоростью (5*0) и соответствующим импульсом. Показать, что продукты ядерного распада будут иметь суммарный импульс, равный начальному».
Т акой
пример полезен в плане осуществления
связи с химией. Задают
импульсы продуктов распада и начальный
импульс ядра атомов.
Решение задачи графически представлено
на рис. 9.
акой
пример полезен в плане осуществления
связи с химией. Задают
импульсы продуктов распада и начальный
импульс ядра атомов.
Решение задачи графически представлено
на рис. 9.
Д алее
целесообразно остановиться на задаче,
например, такой: «Снаряд,
выпущенный из зенитки, взорвался в
верхней точке траектории,
при этом образовалось три осколка, два
из которых разлетелись под прямым углом
друг к другу. Масса первого
алее
целесообразно остановиться на задаче,
например, такой: «Снаряд,
выпущенный из зенитки, взорвался в
верхней точке траектории,
при этом образовалось три осколка, два
из которых разлетелись под прямым углом
друг к другу. Масса первого
![]() ,
а его скорость
,
а его скорость
![]() ,
масса второго
,
масса второго
![]() ,
скорость
,
скорость
![]() ,
а скорость третьего -
,
а скорость третьего -![]() .
Определить
графически направление полета третьего
осколка. Какова
его масса?»
.
Определить
графически направление полета третьего
осколка. Какова
его масса?»
Внимание учащихся обращают на то, что импульс - величина относительная, а закон сохранения импульса справедлив во всех инерциальных системах отсчета. Это важное положение в развитии идеи относительности в механике должно быть закреплено в упражнениях. Например: мяч массой 1 кг движется по футбольному полю со скоростью относительно поля, равной по модулю 4 м/с. Определить его импульс: а) относительно поля; б) относительно футболиста 1, бегущего к мячу со скоростью относительно поля, равной по модулю 5 м/с; в) относительно футболиста 2, ведущего мяч по полю.
Решение: а) Записывают выражение для импульса мяча относительно поля:
![]() ,
,
где
![]() - скорость
мяча относительно поля.
- скорость
мяча относительно поля.
б) Записывают выражение для импульса мяча относительно футболиста 1, бегущего к мячу:
![]() ,
,
где
![]() - модуль скорости футболиста,
- модуль скорости футболиста,
![]() -
модуль скорости мяча относительно
этого футболиста,
-
модуль скорости мяча относительно
этого футболиста,
![]() - модуль
скорости мяча относительно
поля.
- модуль
скорости мяча относительно
поля.
в) Записывают выражение для импульса мяча относительно футболиста 2, ведущего мяч по полю:
![]() ,
,
где
![]() - скорость
мяча относительно этого футболиста.
- скорость
мяча относительно этого футболиста.
Чтобы
показать справедливость закона сохранения
импульса в любой инерциальной системе
отсчета, проведем мысленный опыт.
На платформе, которая движется равномерно
и прямолинейно (![]() -скорость относительно Земли), покоится
тележка массой
-скорость относительно Земли), покоится
тележка массой
![]() (рис.
10). В направлении, противоположном
движению платформы, движется тележка
массой
т2
со
скоростью
(рис.
10). В направлении, противоположном
движению платформы, движется тележка
массой
т2
со
скоростью
![]() относительно
платформы. Скорость
тележек после столкновения
относительно
платформы
относительно
платформы. Скорость
тележек после столкновения
относительно
платформы
![]() .
Предлагаем
учащимся записать ( закон
сохранения импульса в
системе отсчета, связанной
с Землей, и в систем* отсчета,
связанной с платформой,
и выяснить, зависит ли закон сохранения
импульса от выбора
системы отсчета.
.
Предлагаем
учащимся записать ( закон
сохранения импульса в
системе отсчета, связанной
с Землей, и в систем* отсчета,
связанной с платформой,
и выяснить, зависит ли закон сохранения
импульса от выбора
системы отсчета.
Проведенный анализ мысленного опыта позволяет сделать вывод: если закон сохранения импульса выполняется при движении тел относительно одной системы отсчета, то он выполняется и относительно любой другой системы отсчета, движущейся относительно первой равномерно и прямолинейно, т. е. закон сохранения импульса выполняется в любой инерциальной системе отсчета.
Следует
также указать, что при релятивистских
скоростях (![]() )
сумма
релятивистских импульсов, образующих
замкнутую систему,
также остается постоянной при любых
взаимодействиях между телами, только
импульсу зависит от скорости так:
)
сумма
релятивистских импульсов, образующих
замкнутую систему,
также остается постоянной при любых
взаимодействиях между телами, только
импульсу зависит от скорости так:

Целесообразно рассмотреть границы применимости механики Ньютона.
При
скорости, значительно меньшей скорости
света (![]() )отношение
)отношение
![]() ,
поэтому импульс тела равен
,
поэтому импульс тела равен
![]() (это
выражение
справедливо в механике Ньютона).
(это
выражение
справедливо в механике Ньютона).
Завершают изучение закона сохранения импульса рассмотрением реактивного движения. В рамках основного курса достаточно рассмотреть применение закона сохранения импульса для объяснения движения ракеты, для определения ее скорости
![]()
(где
![]() - масса оболочки ракеты,
- масса оболочки ракеты,
![]() -
скорость оболочки ракеты,
т2
и
-
скорость оболочки ракеты,
т2
и
![]() -
соответственно
масса сгоревшего топлива и скорость
истечения газа).
-
соответственно
масса сгоревшего топлива и скорость
истечения газа).
Важно, в воспитательном плане, обратить внимание учащихся на те проблемы, которые возникли в истории ракетостроения.
На факультативных и внеклассных занятиях по физике (в индивидуальной работе с учащимися) можно более детально и обоснованно обсудить указанные проблемы, рассмотрев при этом и такие вопросы, как движение с переменной массой, реактивная сила, более точный расчет максимальной скорости ракеты, многоступенчатость ракет и др.
Материал этой темы благодатен и для воспитательной работы. Здесь следует остановиться на значении работ К.Э.Циолковского, С.П.Королева и других отечественных ученых в развитии космонавтики, на достижениях нашей страны в области освоения космоса.
Эту работу целесообразно проводить как на уроке, так и вне его (специальные стенды, журналы, рассказывающие о достижениях отечественной космонавтики; подбор литературы для чтения учащимися; тематические конференции с докладами и рефератами учащихся и т. д.).
При изучении этого вида механической энергии очень важно, чтобы школьники усвоили, что потенциальная энергия в механике - это энергия взаимодействия по крайней мере двух тел, понятие потенциальной энергии относится к системе тел, а не к одному («изолированному») телу. Это одна из основных задач, которую учитель должен решить при формировании понятия потенциальной энергии. Вторая задача - расширить представления о потенциальной энергии, полученные учащимися в базовом курсе физики: надо показать, что потенциальной энергией обладают не только тела, поднятые над Землей, но и упруго деформированные тела, и дать количественное выражение для потенциальной энергии упруго деформированных тел. И, наконец, третья задача - показать, что выбор нулевого уровня состояния системы (нулевого уровня потенциальной энергии) произволен, так как разность энергий инвариантна относительно этого выбора, хотя потенциальная энергия и зависит от этого выбора.
Остановимся несколько подробнее на первой задаче.
Очень важно довести до понимания учащихся, что потенциальная энергия в механике - это энергия взаимодействия тел, хотя бы двух. Если в системе имеется несколько тел, то потенциальная энергия системы равна сумме потенциальных энергий всех пар взаимодействующих тел (либо тело взаимодействует с каждым из остальных).
Обычно при выводе формулы, связывающей изменение потенциальной энергии с работой сил, одно из тел системы принимают за неподвижное. Например, при рассмотрении падения груза на Землю под действием силы тяжести смещением Земли можно пренебречь. Поэтому работу сил взаимодействия между Землей и грузом сводят к работе только одной силы, действующей на груз. При рассмотрении сжатия или растяжения пружины не учитывают смещения Земли (конец пружины, который закреплен с неподвижным телом, фактически скреплен с Землей). Работу в этом случае совершает лишь сила упругости деформированной пружины, приложенная к телу.
Из-за этого потенциальную энергию системы двух тел учащиеся привыкают рассматривать как энергию одного тела. Это осложняет процесс формирования понятия об этом виде энергии. Чтобы избежать указанных осложнений, правильнее во всех случаях раскрывать следующее положение: изменение потенциальной энергии двух тел, взаимодействующих с силами, зависящими только от расстояния между телами, равно работе этих сил, взятой с противоположным знаком.
Остановимся на методике введения понятия о нулевом уровне потенциальной энергии. При рассмотрении этого вопроса важно выделить следующие моменты:
1. Определяют не саму потенциальную энергию, а ее изменение. Например, для силы тяжести вблизи поверхности Земли:
![]() ,
,
где
![]() и
и
![]() - высота
тела над Землей в начальном и конечном
состояниях.
- высота
тела над Землей в начальном и конечном
состояниях.
Изменение потенциальной энергии деформированной пружины
![]()
где
![]() - коэффициент упругости (жесткость),
- коэффициент упругости (жесткость),
![]() и
и
![]() - начальная и
конечная деформации пружины.
- начальная и
конечная деформации пружины.
Так как работа определяет изменение энергии, а не саму энергию, то только изменение энергии имеет физический смысл. Исходя из этого, можно произвольно выбирать состояния системы, в которых потенциальную энергию можно считать равной нулю. Выбор нулевого уровня, таким образом, произволен и диктуется соображениями удобства (скажем, простотой записи уравнения, выражающего закон сохранения энергии).
2. Часто за нулевой уровень потенциальной энергии (состояние с нулевой энергией) выбирают такое состояние системы, при котором потенциальная энергия минимальна.
Для учащихся целесообразно на примерах показать, что значение потенциальной энергии зависит от выбора начала ее отсчета и что произвольность выбора нулевого уровня не влияет на изменение энергии.
Далее следует показать, что потенциальная энергия не зависит от выбора инерциальной системы отсчета, так как является функцией расстояния между взаимодействующими телами.
Закрепляют
понятия кинетической и потенциальной
энергии при
решении задач. Это могут быть тренировочные
задачи, цель которых
- научить учащихся пользоваться
математическим выражением
для энергии, при этом следует выделить
и те задачи, которые имеют практический
выход. К числу таких задач можно отнести
задачи на определение тормозного пути.
При решении учащихся
знакомят с выражением для тормозного
пути (![]() ),
из которого видно, что тормозной путь
зависит от квадрата
скорости, коэффициента трения и ускорения
свободного падения.
),
из которого видно, что тормозной путь
зависит от квадрата
скорости, коэффициента трения и ускорения
свободного падения.
