Вопрос 35 Гармонические колебания. Дифференциальное уравнение гармонических колебаний. Пружинный, математический и физический маятники.

Периодические колебания называются гармоническими, если колеблющаяся величина меняется с течением времени по закону косинуса или синуса:

.

Здесь - циклическая частота колебаний,A – максимальное отклонение колеблющейся величины от положения равновесия (амплитуда колебаний), φ(t) = ωt+φ₀ – фаза колебаний, φ₀ – начальная фаза.

График гармонических колебаний представлен на рисунке 1.

Рисунок 1 – График гармонических колебаний

При гармонических колебаниях полная энергия системы с течением времени не изменяется. Можно показать, что полная энергия механической колебательной системы при гармонических колебаниях равна:

.

Гармонически колеблющаяся величина s(t) подчиняется дифференциальному уравнению:

, (1)

которое называется дифференциальным уравнением гармонических колебаний.

Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.

- период кодебаний

Физический маятник.

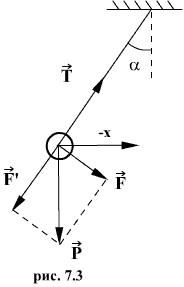
Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.

При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.

Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения

. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:

(7.10)

(7.11)

Решение этого уравнения

Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е.  или

. Из этого соотношения определяем

Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.

Пружинный маятник

Это груз, прикрепленный к пружине, массой которой можно пренебречь.

Пока пружина не деформирована, сила упругостина тело не действует. В пружинном маятнике колебания совершаются под действием силы упругости.

Вопрос 36 Энергия гармонических колебаний

При гармонических колебаниях полная энергия системы с течением времени не изменяется. Можно показать, что полная энергия механической колебательной системы при гармонических колебаниях равна:

.

Потенциальная энергия U тела, смещенного на расстояние х от положения равновесия, измеряется той работой, которую произведет возвращающая сила  , перемещая тело в положение равновесия.

            

Кинетическая энергия

      Заменив в (1.5.2)   и сложив почленно уравнения кинетической и потенциальной энергии, получим выражение для полной энергии:

      Полная механическая энергия гармонически колеблющегося тела пропорциональна квадрату амплитуды колебания.