ЛАБОРАТОРНАЯ РАБОТА №4

Исследование индуктивной катушки и конденсатора цель работы

1. Получить навыки экспериментального определения параметров индуктивной катушки и конденсатора.

2

Рис.3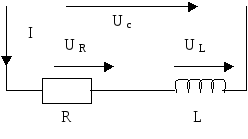

. Освоить методы анализа электрической цепи синусоидального тока с постоянными параметрами R и L (рис.1), а так же конденсатор переменной емкости С (рис.2)

Рис.1

Рис.2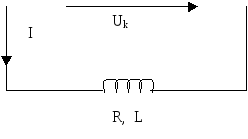

Основные теоретические положения

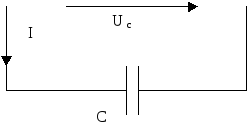
В данной работе исследуются отдельные элементы цепей синусоидального тока - индуктивная катушка с постоянными параметрами R и L (рис.1), а также конденсатор переменной емкости С (рис.2).

При анализе цепи индуктивную катушку представляют в виде эквивалентной схемы замещения, представляющей собой последовательной соединение резистивного элемента c сопротивлением R, равным активному сопротивлению катушки и индуктивного элемента с индуктивностью L, равной индуктивности катушки (рис. 3).

Полное сопротивление катушки Z=Uk/I, где Uk и I - соответствующие значения напряжения тока катушки. Полное сопротивление связано с сопротивлениями схемы замещения следующей формулой:

где Х =wL=2*π*f*l - индуктивное сопротивление катушки;

w = 2*π*f - угловая частота; f - частота тока в цепи (f=50 Гц).

П

Рис.4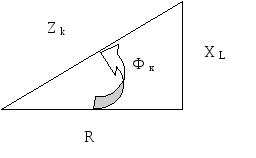

олное сопротивление катушки можно представить как гипотенузу прямоугольного треугольника сопротивлений (рис.4), один катет которого равенR, а другой Х1.

Из треугольника сопротивлений следуют расчетные формулы:

R=Zk*cos(Фk), X=Zk*sin(Фk), Фk=arctg(XL/R)

В соответствии со вторым законом Кирхгофа вектор напряжения индуктивности катушки Uk определяется выражением: Uk=Ur+Ul.

В

Рис.5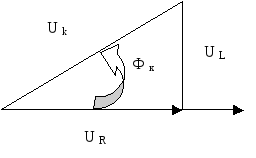

ектор напряжения на резистивном элементе Ur (активная состав­ляющая вектора Uk) совпадает по направлению с вектором тока I. Вектор напряжения на индуктивном элементеUl. (реактивная составляющая вектора Uk) опережает вектор тока I на угол 90". Действующие значения напряжений ur и Ul, , тока I и соответствующие сопротивления катушки связаны следующими формулами: ur=r*i, Ul=Xl*I. Вектор напряжения индуктивной катушки Uk опережает вектор тока I на угол Фк (0<Фк< 90°). Векторная диаграмма тока и напряжений индуктивной катушки приведена на рис.5. Вектор напряжений uk ,Ur ,Ul образуют треугольник напряжений, подобный треугольнику сопротив­лений. На треугольника напряжений можно составить следующие расчетные формулы:

Uk^2=Ur^2+Ul^2, Ur=Uk*cos(Фк), Ul=Uk*sin(Фк), Фк=arctg(Ul/Ur).

Полная мощность катушки Sk по определению равна произведению действующих значений напряжения на катушке Uk и тока катушки I, т.е. Sk= Uk*I. Учитывая, что Uk=Zk*I , получаем Sk=Zk*I^2

Полная мощность Sk связана с активной Р и реактивной ql мощ­ностями индуктивной катушки выражением .

А

Рис.6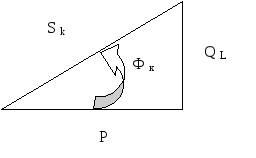

ктивная мощность Р численно равна электрической энергии, преобразующейся в катушке в теплоту за единицу времени, и определяется формулами: Р=R*I^2=Ur*I=Uk*I*cos(Фк)

Реактивная мощность Ql численно равна амплитуде мгновенной мощности, находящейся в процессе обмена между магнитным полем катушки и источником электрической энергии. Величина. реактивной мощности Ql. определяется формулами: Ql=Xl*I^2=Ul*I=Uk*I*sin(Фк)

Графическая связь между sk, Р и ql можно представить в веде прямоугольного треугольника мощностей (рис.6), гипоте­нуза которого равна Sk , а катеты Р и ql Треугольник мощностей подобен треуголь­никам сопротивлений и напряжений.

Из него вытекают следующие соотношения: P=Sk*cos(Фк), Ql=Sk*sin(Фк)

В

Рис.7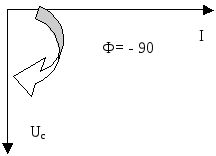

еличинаCOS(Фк) называется коэффициентом мощности, поскольку из треугольника мощностей cos(Фк)=Р/S, т.е. он показывает, какую часть активнея мощность Р .составляет от полной мощности S .

При исследовании конденсатора его представляют, пренебрегая потерями, в виде емкостного элемента, обладающего емкостью С.

Емкостное сопротивление конденсатора Хс=Uc/I , где Uc и I - действующие значения напряжения и тока конденсатора.

Величина Хc зависит от емкости конденсатора С и частоты протекающего в нем тока.

[Ом]

Векторная диаграмма тока в напряжения конденсатора приведена на рис.7. На ней видно, что вектор напряжения на емкостном элементе Uс отстает от векто­ра тока I на угол 90 градусов.

В электрической цепи с емкостным элементом работа не соверша­ется, поэтому активная мощность Р , потребляемая емкостным элементом, равна нулю. Однако в цепи происходит периодический обмен энергией между источником и емкостным элементом. Интенсивность такого обмена характеризуют реактивной мощностью

Qс=Uc*I=Xc*I^2.