ЛЕКЦИЯ №12.
Цепи со взаимной индукцией.
Основные понятия и определения.
Явление наведения эдс в каком-либо контуре (катушке) при изменении тока в другом называется явлением взаимной индукции. При этом если токи протекают в обеих катушках, полное потокосцепление каждой из них:
,
.
Из опыта установлено, что при постоянной магнитной проницаемости среды:
при этом
.
Коэффициент пропорциональности «М» называется коэффициентом взаимной индукции или просто взаимной индуктивностью.
При изменении токов в катушках возникает эдс:
,
,
где е1М и е2М - эдс взаимной индукции, при которой знак «минус» соответствует согласному направлению потоков самоиндукции и взаимной индукции.
Составим отношения
,
.
которые характеризуют долю связанного потока, созданного катушками. Их среднее геометрическое называют коэффициентом связи:
.
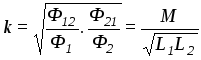Коэффициент связи может находиться в пределах
,
так как
и
.
На практике к максимальному коэффициенту связи стремятся в трансформаторах, где он близок к единице.
Энергия двух катушек при магнитной связи определится как сумма:
и
,
т.е.
.
В общем случае «n» катушек (контуров):
.
Расчет цепей переменного тока при наличии
индуктивных связей.
Пусть в 1-ой катушке
,
а во 2-ой
.
При этом в каждой возникает как эдс самоиндукции, так и эдс взаимной индукции. При их согласном направлении:
,
.
В символической форме:
,
.
При встречном включении
,
.
Уравнения и схемы замещения для магнитно-связанных контуров.
Для расчета необходимо ввести понятие одноименных зажимов. Зажимы называются одноименными, если при одинаковом направлении токов относительно них магнитные потоки само- и взаимоиндукции совпадают. Для катушек это зависит от взаимного расположения и направления намотки. Условно точкой обозначается «начало» катушки.
Индуктивно связанные катушки при параллельном
и последовательном включении.
Для параллельного соединения элементов при согласном и встречном включении ниже приводятся уравнения и векторные диаграммы.
При последовательном соединении
,
где «+» означает согласное включение, а «-» - встречное.
Этот способ соединения может быть применен для определения взаимной индуктивности.
При согласном включении:
,
,
.
При встречном:
,
.
Так как
,
,
то
.
Сложные цепи при наличии индуктивных связей.
При расчете сложных
цепей можно воспользоваться законами
Кирхгофа в символической форме, в составе
которых должны быть напряжения взаимной
индукции вида
.
В соответствии с ранее сделанными
замечаниями положительный знак ставится,
если направление обхода катушки «р»
и тока катушки «q»
относительно одноименных зажимов
совпадают.
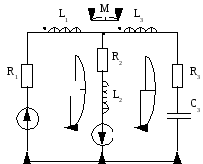
Например, для цепи, изображенной на рисунке, уравнения Кирхгофа принимают вид:
,
,
.
Возможно применение метода контурных токов
,
.
Может быть применен также метод наложения.
Метод узловых потенциалов не применяется, так как основан на 1-ом законе Кирхгофа, не учитывающем напряжения взаимной индукции. Не применяются также методы преобразования и эквивалентного генератора. Однако, и эти методы могут применяться после предварительной «развязки» индуктивных связей. Для этого исключим из уравнений 2-го закона Кирхгофа с помощью 1-го закона токи ветвей, не входящих в контур, для которого они записаны:
,
.
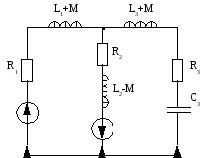
Уравнения принимают вид, которому соответствует изображенная на рисунке электрическая цепь без индуктивных связей:
,
,
.
Трансформаторы в линейном режиме.
Широко используемые
в технике двухобмоточные трансформаторы
представляют собой две индуктивно
связанные катушки, называемые обмотками.
В трансформаторах с сильной связью (
)
обмотки располагают на общем ферромагнитном
сердечнике. Трансформаторы со слабой
связью (k<<1)
без ферромагнитного сердечника называют
воздушными.
Предполагаем отсутствие насыщения сердечника, что делает режим трансформатора линейным.
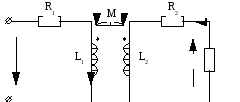
По 2-му закона Кирхгофа
,
.
С учетом линейности получим в комплексной форме:
,
.
Считая известным
,
а также
,
найдем первичный ток. Для краткости
записи положим:
,
,
.
Тогда
,
,
а
.
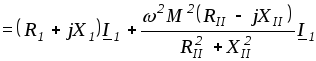Первичный ток
.
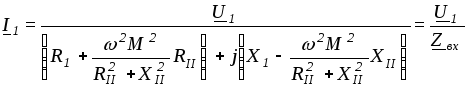В уравнении тока
подчеркнуты так называемые вносимые
активное и реактивное сопротивления.
При
эквивалентное активное сопротивление
больше R1,
что связанно с передачей энергии от
первичной стороны на вторичную.
Эквивалентное реактивное сопротивление
может быть больше X1
, если
XII
<
0
и меньше
X1
, если
XII
>
0.
Представим уравнения
трансформатора в другой форме, вычитая
и добавляя
и
:
,
.
Уравнениям соответствует эквивалентная схема трансформатора, изображенная на рисунке.
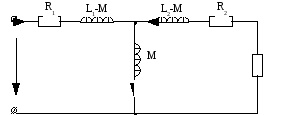
Рассмотрим работу трансформатора при R1=R2=0 и k=1.
Тогда
,
.
Выразим
и
через
и
:
,
.
При
,
.
Обозначим
через С
(
;
).
,
,
т.к
.
Трансформатор,
для которого
при любой нагрузке, называется совершенным.
Если дополнительно
принять
(практически достаточно иметь L1
достаточно
большой , чтобы пренебречь
по сравнению с
),
то
и
.
Трансформатор, для которого соблюдаются эти условия, называется идеальным. Он преобразует токи и напряжения в определенное число раз независимо от сопротивления приемника.
Для идеального трансформатора
,
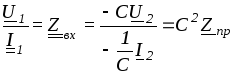т.е. он преобразует сопротивление в определенное число раз, независимо от характера этого сопротивления, что важно при согласовании участков сложных цепей.
Свойствами, близкими к свойства идеального и совершенного трансформаторов, обладают трансформаторы с ферромагнитными сердечниками, с достаточно большим числом витков и большой магнитной проницаемостью ферромагнитного материала.