Теоретические основы электротехники. Базовый конспект лекций для студентов направлений 551300 “Элект / C00K15TO

ЛЕКЦИЯ №15.

Круговые диаграммы цепей переменного тока.

При анализе цепей часто важно знать, как изменяется модуль и аргумент комплексов тока и напряжения в зависимости от изменения параметров цепи. Для решения подобного рода задач широко применяются круговые диаграммы.

При этом необходимо построить годографы (геометрические места) концевых точек векторов, изображающих комплексные величины. В общем случае годографы имеют сложную форму. В простых случае они представляют прямые линии или окружности.

Например, при последовательном соединении комплексных сопротивлений и , если , и неизвестны, а модуль Z₂ сопротивления изменяется от 0 до , комплексное сопротивление ветви

изменяется так , что годограф на комплексной плоскости получается в виде прямой линии.

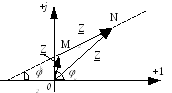
Комплексная проводимость этой ветви

.

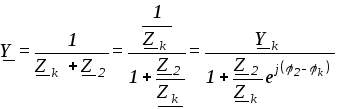Обозначим через и перепишем уравнение в виде:

Рассматривая это уравнение как векторное, замечаем, что сумма двух изменяющихся по величине и по направлению векторов и , а также угол между ними не изменяются. Это возможно только в случае, если годограф конца вектора представляет собой окружность с хордой OM_k . На рисунке показан годограф при .

При Z₂ =0 конец вектора совпадает с точкой М_к (); при Z₂ = - c точкой O (Y = 0). Центр окружности можно найти, исходя из следующих соображений.

Отложим из O по направлению хорды отрезок ОА, равный в некотором масштабе Z_k . Из его конца проведем линию AN¢ под углом к ОА.

Очевидно, что , т.е.

,

или если ОА изображает Z_k , то AN в том же масштабе изображает Z₂. Следовательно AN¢ - линия переменного параметра. Отложив по ней Z₂ и соединив O и N , для любого Z₂ можно определить ОМ. При увеличении Z₂ точка М приближается к О. В пределе при Z₂ ® вектор Y = 0, а точка М сольется с О. При этом секущая ON становится касательной ОТ , а ON будет параллельна ОТ . Поэтому перпендикуляр OD к AN ^/ является также перпендикуляром к OT, т.е. совпадает по направлению с диаметром. Его пересечение со вторым диаметром - перпендикуляром к середине хорды ОМ_к определяет центр окружности.

Рассмотрим теперь простую электрическую цепь из последовательно соединенных Z_к и Z₂ .

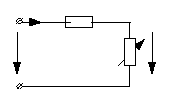
Напряжение и ток связаны соотношениями:

, , где .

Если цепь присоединена к источнику тока J = I = const, то напряжение U изменяется по закону, совпадающему с законом изменения Z. Годографом конца вектора U , будет в этом случае прямая линия. Если же цепь подключена к источнику напряжения U =const, то при изменении Z₂ ток I изменятся по закону, совпадающему с законом изменения комплексной проводимости.

Годограф вектора I  - окружность которую строят следующим образом.

В масштабе m_u на комплексной плоскости откладываем вектор U (на рисунке принят действительным числом).

Вычисляем

и проводим ОM_к - хорду окружности в масштабе m_I .

Выбираем m_z и откладываем

.

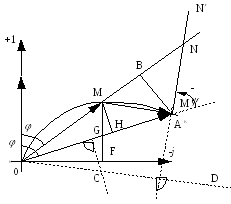
Из точки А(М_к ) под углом

к ОМ_к (или ее продолжению) проводим линию переменного параметра AN ^/. Из точки О проводим OD перпендикулярно AN ^/. Из середины хорды ОМ_к восстанавливаем перпендикуляр до пересечения с OD в точке С - центре окружности. Проводим дугу окружности по ту сторону от хорды, куда направлена линия AN ^/.

Для любого Z₂ ток определится, если отложить по AN ^/ отрезок и точку N соединить с точкой О.

Напряжение на постоянном сопротивлении

пропорционально току. Поэтому ОМ в другом масштабе изображает модуль U_k (но не фазу !). Масштаб U_k определим при коротком замыкании переменного сопротивления (Z₂ = 0). Тогда ОМ становится ОM_к и . Следовательно, .

Отрезок ММ_к в том же масштабе определяет модуль (но не фазу !) напряжения , так как

.

Длина перпендикуляра MF определяет активную мощность цепи, т.к.

.

Отрезок OF в том же масштабе изображает реактивную мощность, т.к.

.

Мощности , и могут определяться отрезком MG или MН. В самом деле , опустив перпендикуляр на ON^/ , имеем площадь треугольника ОММ_к :

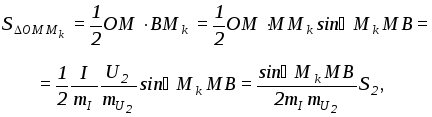
т.е. площадь треугольника пропорциональна полной мощности, т.к. =const. Но , а . Поэтому при постоянстве j₂ эти же отрезки выражают также Р₂ и Q₂.

Масштабы определяются по частному режиму.

Этот же способ построения круговой диаграммы может быть применен и для разветвленных цепей, если выразить ток одной из ветвей с помощью теоремы об активном двухполюснике в виде:

,

т.е.

,

где

.

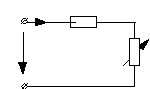
Подобным приемом задача построения диаграммы сводится к неразветвленной цепи, аналогично рассмотренной.