ЛЕКЦИЯ №9.
Последовательное соединение R, L, C в цепи переменного тока.
При
токе
напряжения на участках :
-
на активном сопротивлении,
- на индуктивности,
-
на емкости.
В соответствии с последовательным соединением:
.
Обозначим
.
При этом возможны случаи:
,
и
.
Очевидно, напряжение источника в общем случае
где j может принимать любые значения от 0 до 900 .
Продолжим анализ первого случая.
Из диаграммы следует
,
где
-
полное сопротивление.
При этом
,
или
.
Условно при UL > Uc (ток отстает от напряжения) угол сдвига фаз считается положительным, а при UL < Uc (ток опережает напряжение) угол считается отрицательным. Этому соответствует вполне определенная запись начальных фаз напряжения и тока: за исходную - принимается напряжение
.
Тогда ток всегда записывается в виде
,
(при этом в состав обозначения угла j входит знак).
При UL = Uc (XL = Xc) напряжение и ток совпадают по фазе. Такой режим называют резонансным.
От векторной диаграммы легко перейти к треугольнику сопротивлений (например, уменьшением всех ее сторон в I раз).
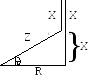
Нетрудно
заметить, что в треугольнике Z
является
гипотенузой , R
- прилежащим к углу j
катетом, а
X
- противолежащим.
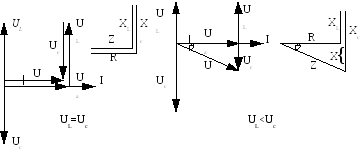
Ниже приведены векторные диаграммы и треугольники сопротивлений для второго и третьего случаев.
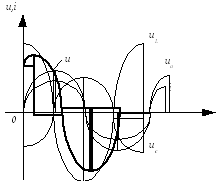
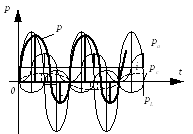
Мгновенная мощность цепи
.
При
мгновенная мощность
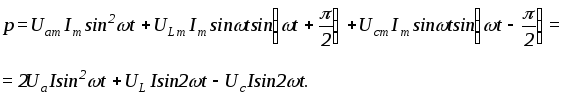
В цепи происходит в разные промежутки времени как обмен энергией между полями и генератором, так и преобразование ее в тепловую энергию.
Средняя за период или активная мощность
,
Вт,
реактивная мощность
,
вар,
полная мощность
,
В А.
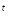Мощности
связаны между собой также как стороны
прямоугольного треугольника (на рисунке
представлен треугольник мощностей для
первого случая). Из него следует
.
Цепи переменного тока с параллельно включенными элементами.
Метод проводимостей.
Пусть
Тогда
При этом
,
где
.
Обратные полным сопротивлениям величины называются полными проводимостями:
.
Ток
в неразветвленной части
.
Из векторной диаграммы следует
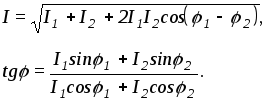
Такой способ определения токов при большом числе параллельных ветвей оказывается громоздким.
Рассмотрим ток ветви как сумму двух составляющих
и
,
где
- активная проводимость первой ветви
- реактивная
проводимость первой ветви.
Аналогично:
,
где
,
,
где
.
Тогда
,
,
где
.
Нетрудно заметить, что проводимости связаны между собой как стороны прямоугольного треугольника проводимостей. Из него следует:
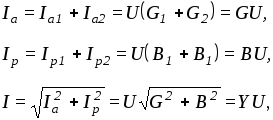
где
Мощности
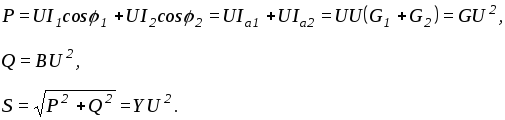
При нескольких параллельных ветвях задача решается аналогично с учетом того , что реактивная емкостная проводимость отрицательна.
Решая уравнение
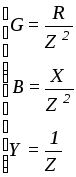
относительно R, X, Z, получим возможность определить по проводимостям эквивалентные сопротивления ветви:
