
ЛЕКЦИЯ №14.
Резонанс в сложных цепях.
В общем случае при резонансе ток и напряжение на зажимах резонансного участка совпадают по фазе, несмотря на наличие реактивных элементов.
Для отыскания
связи между частотой и параметрами цепи
при резонансе необходимо найти выражение
для реактивного сопротивления Х
или для
реактивной проводимости В
и приравнять
то или другое нулю. Очевидно, что при
![]() ,
если Х = 0,
то и
,
если Х = 0,
то и
![]() .
.
В идеализированных случаях чисто реактивных цепей условия Х = 0 и В = 0 не однозначны. Тогда условиями резонанса будут
1.![]() и
и
![]() или
или
2.
![]() и
и
![]() .
.
Применимость того или иного условия определяется конфигурацией цепи. Например, для простейших цепей
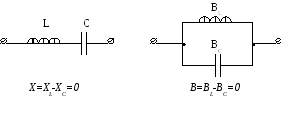
Рассмотрим случай резонанса при смешанном соединении сопротивлений. Комплексная проводимость
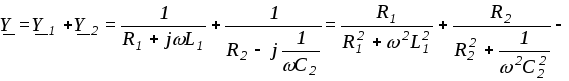
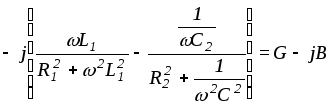 .
.

Из условий резонанса при В = 0 получим
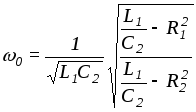 .
.
Такую же зависимость можно получить и приняв Х = 0 по уравнению
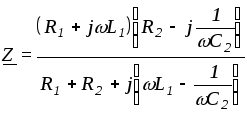 .
.
Это условие резонанса отличается от простейшего и совпадает с ним только при R1 = R2 .
Энергетическая
сторона так же отличается от рассмотренных
ранее случаев. При
![]() и
и
![]() ,
т.е. в цепь поступает энергия. При этом
сумма энергий электрического и магнитного
полей не остается постоянной, т.е. имеются
промежутки времени, когда энергия от
источника переходит в энергию
электрического и магнитного полей,
имеются так же промежутки времени, когда
энергия электрического и магнитного
полей преобразуется в тепловую на
активных сопротивлениях. Однако, возврата
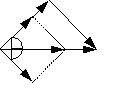
энергии генератору нет. На диаграмме
представлен случай когда обмена энергией
между полями вообще нет, т.к.
,
т.е. в цепь поступает энергия. При этом
сумма энергий электрического и магнитного
полей не остается постоянной, т.е. имеются
промежутки времени, когда энергия от
источника переходит в энергию
электрического и магнитного полей,
имеются так же промежутки времени, когда
энергия электрического и магнитного
полей преобразуется в тепловую на
активных сопротивлениях. Однако, возврата
энергии генератору нет. На диаграмме
представлен случай когда обмена энергией
между полями вообще нет, т.к.
![]() и
и
![]() находятся в фазе, а поэтому
находятся в фазе, а поэтому
![]() и
и
![]() одновременно возрастают и убывают.
одновременно возрастают и убывают.
Резонанс в индуктивно связанных контурах.
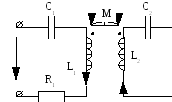
Для упрощения задачи будем пренебрегать активным сопротивлением 2-го контура. При отсутствии взаимной индукции резонансные частоты
![]() ,
,
![]() .
.
Составим уравнения при наличии взаимной индукции
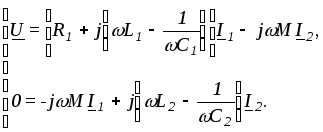
Определим из
второго уравнения
![]() и подставим в первое:
и подставим в первое:
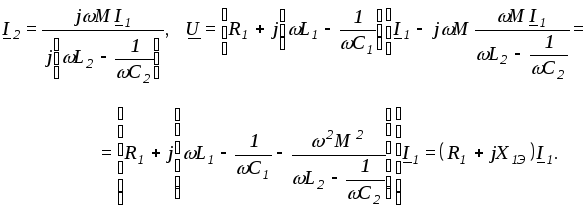
По условию резонанса
![]() ,
т.е.
,
т.е.
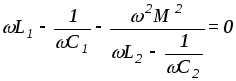 ,
,
или
![]() .
.
Разделим обе части
на
![]()
![]() .
.
Тогда
![]() ,
,
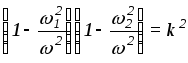 ,
где k
< 1.
,
где k
< 1.
Определим резонансную частоту
![]() ,
,
или
![]() .
.
Резонансная частота
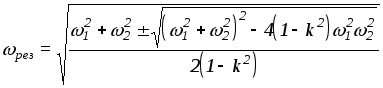 .
.
Если оба контура предварительно настроены на одинаковую частоту
![]() ,
,
то
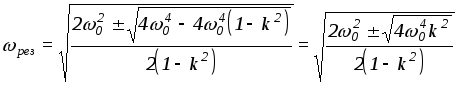 .
.
Или окончательно
![]() ,
,
т.е.
![]() ,
,
![]() .
.
При
![]() эквивалентное реактивное сопротивление
эквивалентное реактивное сопротивление
![]() и
и
![]() .
.
При
![]() и при
и при
![]() ,
,
![]() .
Из второго уравнения следует, что при
конечном значении тока
.
Из второго уравнения следует, что при
конечном значении тока
![]() эдс
эдс
![]() ,
т.е.
,
т.е.
![]() .
Ток
.
Ток
![]() устанавливается таким, чтобы эдс
уравновесила бы приложенное напряжение
(уравнение 1).
Этот случай аналогичен резонансу токов
в контуре без потерь.
устанавливается таким, чтобы эдс
уравновесила бы приложенное напряжение
(уравнение 1).
Этот случай аналогичен резонансу токов
в контуре без потерь.
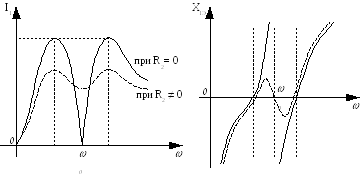
На характеристиках
пунктиром нанесены их вид при R2![]() 0.
0.
