Задача локализации

Задан многоугольник, ограниченный несамопересекающейся замкнутой ломаной P1P2...Pn и некоторая точка A(x, y). Требуется определить, содержится ли эта точка внутри многоугольника или нет.

Для проверки принадлежности точки выпуклому многоугольнику переносим начало координат в точку масс, рассчитываем точки пересечения сторон многоугольника с осями координат и оцениваем положение точки относительно многоугольника, сравнивая «знаки расстояний» по осям.

Определение принадлежности точки непересекающемуся многоугольнику

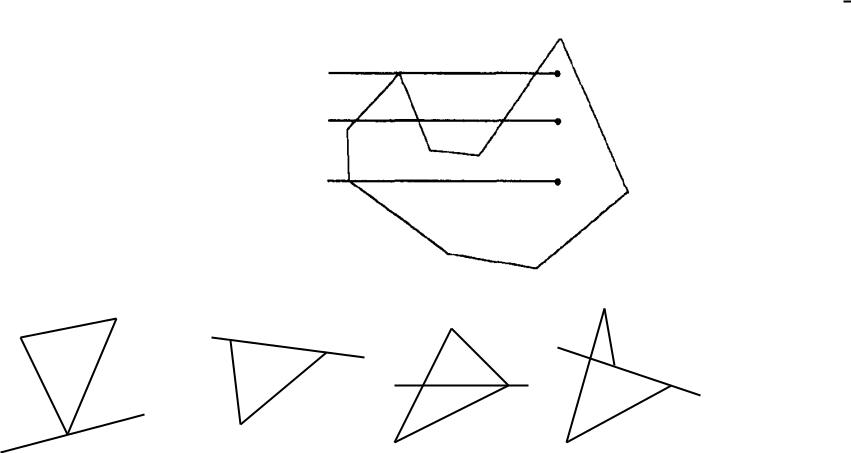
Частные случаи прохождения луча: а – через вершину; б – через сторону;

в – через вершину с пересечением; г – через сторону с пересечением

Подсчет числа пересечений

int PtInPoly(Point& a, Point *p, int n)

{

int Count = 0:

for (int i = 0: i < n; i++)

{

int j = (i + 1) » n;

if (p[i].y == p[j].y ) continue;

if (p[i].y > а.у && p[j].y > а.у) continue; if (p[i].y < а.у && p[j].y < а.у) continue; if (max(p[i].y, p[j].y) == а.у) Count++; else

if (min(p[i].y, p[j].y) == а.у) continue: else

{double t = (у - p[i].y) / (p[jl.y - p[i].y);

}if (t>0 && t<1 && p[i].x + t*(p[j].x-p[i].x) >= x) Count++;

}

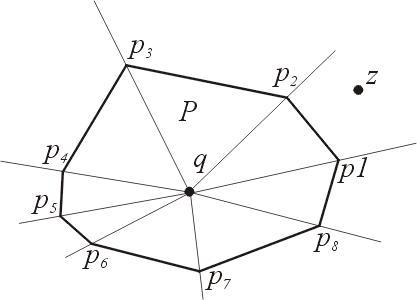
Случай массового запроса задачи локализации

Процедура поиска:

1.Дана пробная точка z. Определяем методом двоичного поиска клин, в котором она лежит. Точка z лежит между лучами,

определяемыми pi и pi+1, тогда и только тогда, когда угол (zqpi+1) положительный, а угол (zqpi) отрицательный.

2.Если pi и pi+1 найдены, то z – внутренняя точка тогда и только тогда, когда угол (pipi+1z) отрицательный.

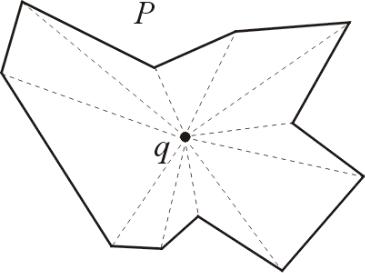
Звездный многоугольник

Построение выпуклой оболочки

Простейший алгоритм:

•Определить крайние точки.

•Упорядочить эти точки так, чтобы они образовали выпуклый многоугольник.

Теорема 1. Точка p не является крайней точкой множества S только тогда, когда она лежит в некотором треугольнике, вершины которого принадлежат S, но сама она не является вершиной этого треугольника.

Теорема 2. Последовательные вершины выпуклого многоугольника располагаются в порядке, соответствующем изменению угла относительно любой внутренней точки.