83

5. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

Вывод изображения на экран дисплея и разнообразные действия с ним, в том числе и визуальный анализ, требуют от пользователя известной геометрической грамотности. Геометрические понятия, формулы и факты, относящиеся прежде всего к плоскому и трехмерному случаям, играют в задачах компьютерной графики особую роль. Геометрические соображения, подходы и идеи в соединении с постоянно расширяющимися возможностями вычислительной техники являются неиссякаемым источником существенных продвижений на пути развития компьютерной графики, ее эффективного использования в научных и иных исследованиях. Порой даже самые простые геометрические методики обеспечивают заметные продвижения на отдельных этапах решения большой графической задачи.

5.1. Преобразования на плоскости и в пространстве

Для решения таких задач, как движение объектов и их частей, управления камерой применяются аффинные преобразования (АП), рассмотрим их основные свойства:

1)точки, лежащие на одной прямой, после преобразования лежат на одной прямой;

2)пересекающиеся прямые остаются пересекающимися, а параллельные – параллельными;

3)при АП пространства пересекающиеся плоскости остаются пересекающимися, параллельные – параллельными, а скрещивающиеся – скрещивающимися;

4)при АП сохраняются отношения площадей двух квадратов на плоскости и отношение объемов двух кубов в пространстве.

Аффинные преобразования на плоскости

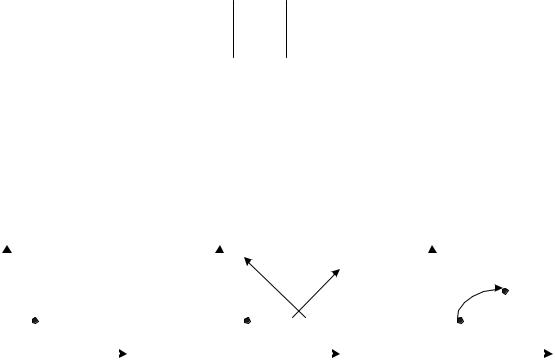
Допустим, на плоскости задана прямолинейная координатная система. Тогда каждой точке М соответствует упорядоченная пара чисел (х, у) ее координат (рис. 5.1). Вводя на плоскости еще одну прямолинейную систему координат, мы ставим в соответствие той же точке М другую пару чисел – (х*, у*).

Переход от одной прямолинейной координатной системы на плоскости к другой описывается следующими соотношениями:

x* =αx + β y +λ,

(1)

y* =γ x +δ y + µ,

84

где α, β, λ, γ, µ, δ – произвольные числа, связанные неравенством

α β ≠ 0.

γδ

Формулы (1) можно рассматривать двояко: либо сохраняется точка и изменяется координатная система (рис. 5.2) (в этом случае произвольная точка М остается той же, изменяются лишь ее координаты), либо изменяется точка и сохраняется координатная система (рис. 5.3) (в этом случае формулы (1) задают отображение, переводящее произвольную точку M(x,y) в точку М*(х*, у*), координаты которой определены в той же координатной системе).

Вдальнейшем мы будем рассматривать формулы (1) как правило, согласно которому в заданной системе прямолинейных координат преобразуются точки плоскости.

Ваффинных преобразованиях плоскости особую роль играют несколько важных частных случаев, имеющих хорошо прослеживаемые геометрические характеристики. При исследовании геометрического смысла числовых коэффициентов в формулах (1) для этих случаев удобно считать, что заданная система координат является прямоугольной декартовой.

1.Поворот вокруг начальной точки на угол ϕ описывается формулами

x* = xcosϕ − ysinϕ,

y* = xsinϕ + y cosϕ.

2.Растяжение (сжатие) вдоль координатных осей можно задать так:

x* =αx, y* =δ y, α > 0, δ > 0.

Растяжение вдоль оси абсцисс обеспечивается при условии, что α > 1, а сжатие – при 0 < α < 1.

85

3.Отражение (относительно оси абсцисс) задается при помощи

формул

x* = x, y* = −y .

4.Параллельный перенос обеспечивают соотношения

x* = x +λ, y* = y + µ.

Выбор этих четырех частных случаев определяется двумя обстоятельствами.

1.Каждое из приведенных выше преобразований имеет простой и наглядный геометрический смысл (геометрическим смыслом наделены и постоянные числа, входящие в приведенные формулы).

2.Как доказывается в курсе аналитической геометрии, любое преобразование вида (1) всегда можно представить как по-

следовательное исполнение простейших преобразований. Для эффективного использования этих известных формул в за-

дачах компьютерной графики более удобной является их матричная запись. Матрицы, соответствующие случаям А, Б и В, строятся легко и имеют соответственно следующий вид:

Однако для решения рассматриваемых далее задач весьма желательно охватить матричным подходом все четыре простейших преобразования (в том числе и перенос), а значит, и общее аффинное преобразование. Этого можно достичь, например, так: перейти к описанию произвольной точки плоскости, не упорядоченной парой чисел, как это было сделано выше, а упорядоченной тройкой чисел.

Однородные координаты точки

Пусть М – произвольная точка плоскости с координатами х и у, вычисленными относительно заданной прямолинейной координатной системы. Однородными координатами этой точки называется любая тройка одновременно неравных нулю чисел x1, x2, x3, связанных с заданными числами x и y следующими соотношениями:

x1 / x3 = x, x2 / x3 = y .

86

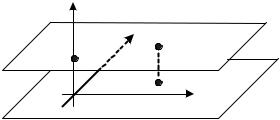
При решении задач компьютерной графики однородные координаты обычно вводятся так: произвольной точке М(х, у) плоскости ставится в соответствие точка М*(х, у, 1) в пространстве (рис. 5.4).

Заметим, что произвольная точка на прямой, соединяющей начало координат, точку O(0, 0, 0) с точкой M*(х, у, 1), может быть задана тройкой чисел вида (hx, hy, h).

Рис. 5.4. Однородные координаты

Будем считать, что h≠0. Вектор с координатами hx, hy, h является направляющим вектором прямой, соединяющей точки 0(0, 0, 0) и М*(х, у, 1). Эта прямая пересекает плоскость z = 1 в точке (х, у, 1), которая однозначно определяет точку (х, у) координатной плоскости ху.

Тем самым между произвольной точкой с координатами (х, у) и множеством троек чисел вида (hx, hy, h) при h≠0 устанавливается (взаимно однозначное) соответствие, позволяющее считать числа hx, hy, h новыми координатами этой точки.

В проективной геометрии для однородных координат принято следующее обозначение: x : у : 1 или x1 : x2 : x3 (числа x1, x2, x3 одновременно в ноль не обращались).

Применение однородных координат оказывается удобным уже при решении простейших задач, например, масштабирования:

1)точку с однородными координатами (0.5; 0.1; 2.5) h=1 нельзя представить целыми координатами, но, например, при выборе h=10 получаем (5; 1; 25);

2)чтобы результаты преобразования не приводили к арифметическому переполнению, для точки с координатами

(80000;40000;1000) можно взять, например, h=0,001. В ре-

зультате получим (80;40;1).

Приведенные примеры показывают полезность использования однородных координат при проведении расчетов. Однако основной целью введения однородных координат в компьютерной графике является их несомненное удобство в применении к геометрическим преобразованиям.

87

При помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование плоскости.

В самом деле, считая h = 1, сравним две записи: помеченную символом * и следующую, матричную:

Нетрудно заметить, что после перемножения выражений, стоящих в правой части последнего соотношения, мы получим обе формулы (1) и верное числовое равенство 1 ≡ 1. Тем самым сравниваемые записи можно считать равносильными.

Элементы произвольной матрицы аффинного преобразования не несут в себе явно выраженного геометрического смысла. Поэтому, чтобы реализовать то или иное отображение, то есть найти элементы соответствующей матрицы по заданному геометрическому описанию, необходимы специальные приемы. Обычно построение этой матрицы в соответствии со сложностью рассматриваемой задачи разбивают на несколько этапов.

На каждом этапе находят матрицу, соответствующую тому или иному из выделенных выше случаев А, Б, В или Г, обладающих хорошо выраженными геометрическими свойствами.

Выпишем соответствующие матрицы третьего порядка.

Рассмотрим примеры аффинных преобразований плоскости.

88

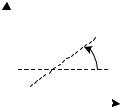
Пример 1. Построить матрицу поворота

возвращения центра поворота в прежнее положение; матрица соответствующего преобразования.

Перемножим матрицы в том же порядке, как они выписаны: [T- A][Rϕ][TA]. В результате получим, что искомое преобразование (в матричной записи) будет выглядеть следующим образом:

Элементы полученной матрицы (особенно в последней строке) не так легко запомнить. В то же время каждая из трех перемножаемых матриц по геометрическому описанию соответствующего отображения легко строится.

Пример 2. Построить матрицу растяжения с коэффициентами растяжения α вдоль оси абсцисс и β вдоль оси ординат и с центром в точке А(а, b).

1-й шаг. Перенос на вектор А(-а, -b) для совмещения центра растяжения с началом координат.

2-й шаг. Растяжение вдоль координатных осей с коэффициентами α и β соответственно.

3-й шаг. Перенос на вектор А(а, b) для возвращения центра растяжения в прежнее положение; матрица соответствующего преобразования.