Формула Дарси – Вейсбаха – определяет величину потерь напора на трение при движении жидкости в круглых трубах:

где - коэффициент гидравлического трения, и - длина и диаметр трубы, - средняя скорость течения, - ускорение свободного падения. В случае некруглых труб…..

Формула Пуазейля – определяет падение давления на участке круглой цилиндрической трубы длинойпри установившемся ламинарном течении жидкости:

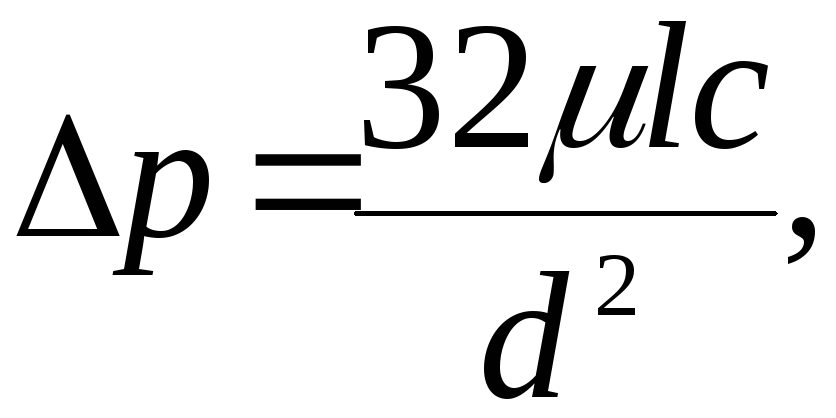
где - коэффициент динамической вязкости,- диаметр трубы, - скорость течения жидкости. Формулу Пуазейля нельзя применять для расчета потери напора на начальном участке трубы, так как здесь не выполняется условие прямолинейности линий тока.

Формула Сен-Венена – Ванцеля – формула, определяющая скорость истечения газа из резервуара через сужающееся сопло (размеры резервуара считаются настолько большими по сравнению с размером отверстия сопла, что газ в резервуаре можно считать покоящимся):

где и– давление и температура газа в резервуаре,– давление за соплом,– газовая постоянная,– показатель адиабаты. При давлении на срезе соплагде– критическое давление, скорость истечения газа из резервуара достигнет максимального значения, равного критической скоростипри данных параметрах газа в резервуаре:

Формула Стокса – одна из основных интегральных теорем векторного анализа, связывающая поверхностный интеграл с криволинейным; математическая формула, которая выражает циркуляцию векторного поля вдоль замкнутого контурачерез поток ротора этого поля через поверхность, ограниченную этим контуром:

.

Формула Торричелли– определяет скорость истечения идеальной жидкости из малого отверстия в открытом сосуде: где– высота уровня жидкости, отсчитываемая от центра отверстия;– ускорение свободного падения. Из формулы Торричелли следует, что скорость истечения жидкости из отверстия одинакова для всех жидкостей и зависит только от высоты, т. е. равна скорости падения тела с этой же высоты. Действительная скорость истечения отличается от скорости, определяемой формулой Торричелли: она зависит от формы и размеров отверстия, от вязкости жидкости и величины расхода, Для учета этих факторов в формулу Торричелли вводят поправочный множитель, меньший единицы. Тогда формула приобретает вид:. Множительназывается коэффициентом скорости при истечении жидкости из отверстия.

Ц

Центр водоизмещения – центр тяжести массы жидкости в объеме погруженной части тела.

Центр давления – точка, в которой линия действия равнодействующей приложенных к покоящемуся или движущемуся телу сил давления окружающей среды (жидкости, газа) пересекается с некоторой проведенной в теле плоскостью. Например, для крыла самолета центр давления определяют как точку пересечения линии действия аэродинамической силы с плоскостью хорд крыла. Положение центра давления зависит от формы тела, а у движущегося тела от направления и скорости движения и от свойств окружающей среды (её сжимаемости).

Циркуляция вектора скорости – кинематическая характеристика течения жидкости или газа, которая служит мерой завихренности течения. Циркуляция связана с вращением элементарного объема жидкости (газа) при его деформации в процессе движения. Циркуляция вектора скорости представляется криволинейным интегралом по замкнутому контуру L от произведения проекции скорости на касательную к кривой на элемент длины этой кривой:

где - циркуляция вектора скорости по контуруL, - скорость частицы,- проекции скорости на оси координат,- элемент длины кривой. Согласно формуле Стокса циркуляция вектора скорости связана с потоком вектора вихря скоростичерез произвольную поверхность, опирающуюся на кривуюL, равенством

Если циркуляция вектора скорости по любому замкнутому контуру, проведенному внутри жидкости, равна нулю, то течение жидкости будет безвихревым, или потенциальным.

Ч

Число Кнудсена () – один из критериев подобия движения разреженных газов, , где– средняя длина свободного пробега молекулы в газе,– характерный размер течения. Если<< 1, справедливо основное положение механики жидкости и газа – гипотеза сплошности.

Число Маха – характеристика течения газа, равная отношению скорости течения к скорости звукав той же точке потока:. Число Маха является одним из основных критериев подобия в гидроаэромеханике и является мерой влияния сжимаемости газа на его движение. Можно показать, что ~, т.е. относительное изменение плотности в газовом потоке пропорционально. При <<1 газы можно считать несжимаемыми. Величина числа Маха принята за основу классификации течений газа: при 0 газ можно считать несжимаемым; при < 1 течения называются дозвуковыми, при ≈ 1 – околозвуковыми, при > 1 – сверхзвуковыми и при > 5 – гиперзвуковыми. Число Махасвязано сприведенной скоростью иотносительной скоростью следующими соотношениями:

где – показатель адиабаты.

Число Рейнольдса – один из критериев подобия для течений вязких жидкостей и газов, характеризующий соотношение между силами инерции и силами вязкости:

Re = c/, где c – характерная скорость потока, - характерный линейный размер, - коэффициент кинематической вязкости. Число Рейнольдса используется в гидродинамике для моделирования гидродинамических явлений. Число Рейнольдса является одной из характеристик течения вязкой жидкости (или газа). Для каждого вида течения существует такое критическое число Рейнольдса Re_кр, что при Re<Re_кр возможно только ламинарное течение, а при Re>Re_кр течение может стать турбулентным. Например, для течения вязкой жидкости в круглой цилиндрической трубе Re_кр = 2300.

Число Струхаля – критерий подобия нестационарных движений жидкости или газа, характеризует отношение локальной инерционной силы к конвективной:

где - характерный линейный размер течения,- характерная скорость течения,- характерный для нестационарного движения промежуток времени.

Число Фруда Fr – один из критериев подобия движения жидкостей или газов, характеризует соотношение между инерционной силой и силой тяжести:

где – характерная скорость течения или скорость движущегося тела,– характерный размер потока или тела,– ускорение силы тяжести. Условие подобия – равенство чисел Фруда для модели и для натурных объектов – применяют при моделировании движения кораблей, течений воды в открытых руслах, испытаниях моделей гидротехнических сооружений и др. При моделировании газовых потоков число Фруда обычно не входит в число определяющих критериев подобия.

Число Эйлера Еи – один из критериев подобия движения жидкостей или газов, характеризующий соотношение между силами давления, действующими на элементарный объем жидкости или газа, и инерционными силами:

где – давление,– плотность жидкости или газа,– скорость течения. В сжимаемых газовых потоках число Эйлера связано с другим критерием подобия – числом МахаМ и отношением удельных теплоемкостей среды формулой где(– удельная теплоемкость при постоянном давлении,– удельная теплоемкость при постоянном объеме).

Э

Электрогидравлический удар - возникновение высокого давления в результате высоковольтного электрического разряда между электродами, погруженными в жидкость.

Электрогидравлический удар используется для механического воздействия на материалы.

Энергия - скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие.

Энтальпия (теплосодержание) – однозначная функция состояния термодинамической системы, термодинамический потенциал, характеризующий термодинамическое состояние макроскопической системы в термодинамическом равновесии при выборе в качестве основных независимых переменных энтропии и давления . Энтальпия связана с внутренней энергией системы соотношением H = U + V, где V – объём системы. При постоянном давлении изменение энтальпии равно количеству теплоты, подведённой к системе. Энтальпия идеального газа зависит от его температуры: Н = 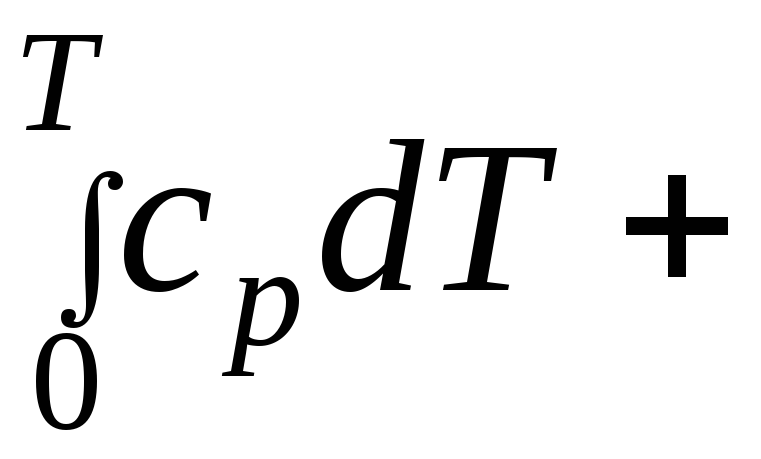Н₀, где –теплоёмкость при постоянном давлении, Н₀ – энтальпия при Т = 0. Равновесному состоянию системы при постоянных значениях давления и энтропии соответствует минимальное значение энтальпии. Термодинамический процесс, в котором энтальпия не изменяется, называется изоэнтальпийным. Энтальпия - аддитивная функция.

Энтропия – функция состояния термодинамической системы S, изменение которой в равновесном процессе равно отношению количества теплоты dQ, сообщаемого системе или отведенного от нее, к термодинамической температуре системы T: dS = dQ/T. Введена Р.Клаузиусом на основе второго начала термодинамики для определения меры необратимого рассеяния энергии. Разность значений энтропии идеального газа в двух произвольных состояниях А и В равна где – масса газа, – молярная масса газа, и , и – температура и объём газа соответственно в состояниях и – молярная теплоёмкость газа при постоянном объёме, – универсальная газовая постоянная. Л.Больцман дал статистическое толкование энтропии, определив её как меру вероятности осуществления какого-либо макроскопического состояния, как меру неупорядоченности (беспорядка) термодинамической системы: S = k∙lnP, где k - постоянная Больцмана, P – статистический вес системы (см.). Согласно второму началу термодинамики, в изолированных системах энтропия не может убывать. При необратимых процессах в изолированной системе энтропия может только возрастать (принцип возрастания энтропии). При приближении к состоянию равновесия неупорядоченность системы и статистический вес системы возрастают, в состоянии равновесия энтропия системы максимальна. Согласно теореме Нёрнста энтропия равновесной системы при стремлении температуры к абсолютному нулю стремится к конечному пределу, не зависящему от давления, плотности, других термодинамических параметров или фазы; этот предел считается равным нулю: