
- •Министерство образования российской федерации
- •Теория вероятностей и математическая статистика
- •Предисловие
- •1. Случайные события
- •§1. Элементы комбинаторики
- •§2. Классическое и статистическое определение вероятности
- •§3. Операции над событиями
- •§4. Теоремы сложения и умножения вероятностей
- •§5. Формулы полной вероятности и бейеса
- •§6. Формула бернулли
- •§7. Элементы теории структурной надёжности
- •2. Случайные величины
- •§8. Дискретные случайные величины
- •§9. Непрерывные случайные величины
- •§10. Биномиальное распределение
- •§11. Распределение пуассона. Простейший поток событий
- •§12. Равномерное распределение
- •§13. Показательное распределение
- •§14. Нормальное распределение
- •§15. Теоремы группы цпт
- •§16. Двумерные случайные величины
- •§17. Функции случайных величин
- •M[y] (m[X]); d[y] [’(m[X])]2d[X];
- •М[y] (m[х1], m[х2], …,m[Хn]),
- •§18. Закон больших чисел
- •3. Математическая статистика
- •§19. Основы выборочного метода
- •§20. Элементы корреляционного анализа
- •§1. Элементы комбинаторики
- •§2. Классическое и статистическое определение вероятности
- •§3. Операции над событиями
- •§4. Теоремы сложения и умножения вероятностей
- •§9. Непрерывные случайные величины
- •§17. Функции случайных величин
- •§18. Закон больших чисел
- •§19. Основы выборочного метода
- •§20. Элементы корреляционного анализа
- •Список рекомендуемой литературы
- •Приложения
- •Оглавление
§9. Непрерывные случайные величины
9.1.
М[Х]
=
![]() ;
D[X] =
;
D[X] =![]() ;σ[X]
=
;σ[X]
=
![]() ;
Р{0 < Х
;
Р{0 < Х![]() 1,5} = 0,25;9.2. a =
1,5} = 0,25;9.2. a = ![]() ;М[X]
= 0; D[X] =
;М[X]
= 0; D[X] =
![]() ;σ[X]
=
;σ[X]
=
![]() ;
;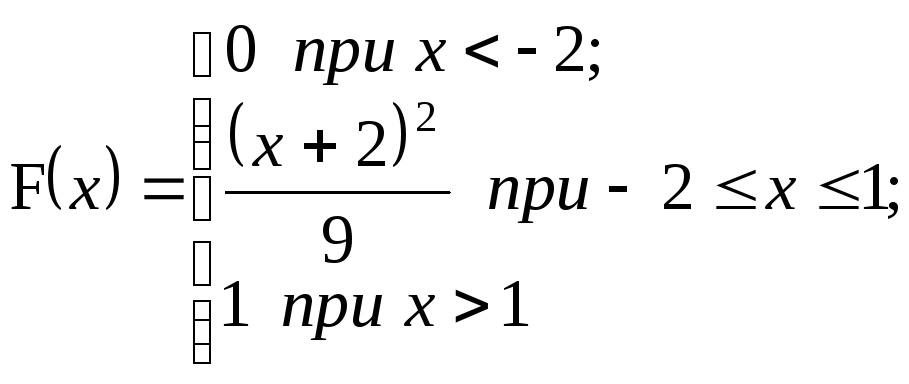 Р{Х ≤ 0}
=
Р{Х ≤ 0}
=
![]() ;
Р{Х = –1} = 0;
Р{Х > 0,5}
=
;
Р{Х = –1} = 0;
Р{Х > 0,5}
=
![]() ;
9.3.
;
9.3.
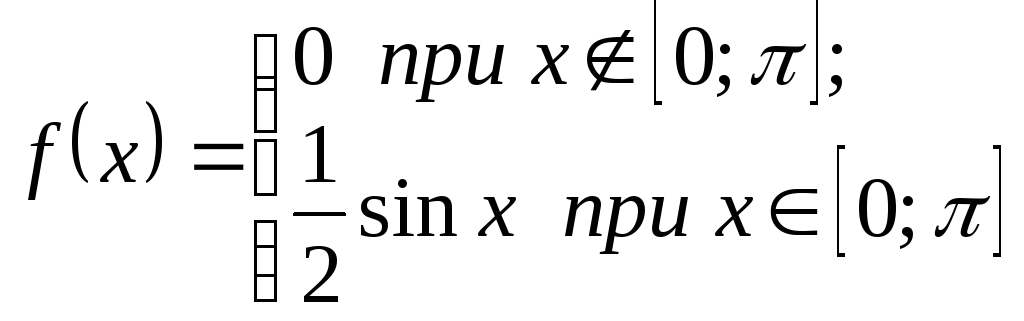 ;
;
![]() ;
9.4.
а =
;
9.4.
а = ![]() ;b =
;b = ![]() ;
;
![]() ;
Р{0 ≤ Х ≤ 1}
=
;
Р{0 ≤ Х ≤ 1}
=
![]() ;
9.5. а = 1;
;
9.5. а = 1;
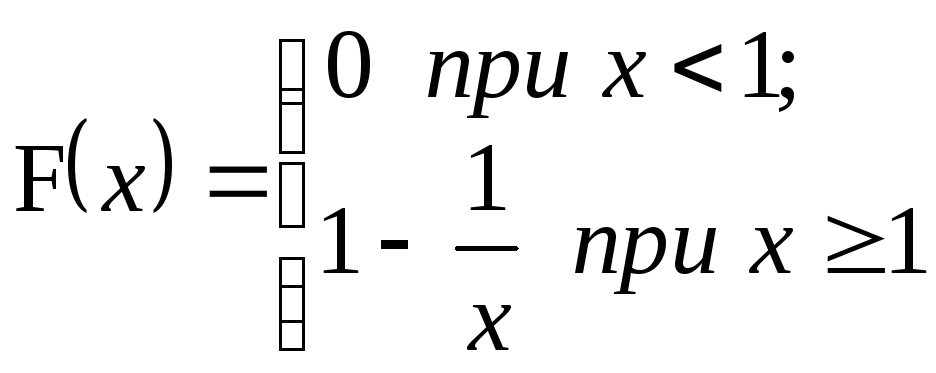 ;
P{2 < X < 3} =
;
P{2 < X < 3} =![]() ;9.6.
;9.6.
![]() ;
;![]() ;9.7.
;9.7.
![]() ;М[Х]
=
;М[Х]
=
![]() ;
D[X] =
;
D[X] =![]() ;σ[X]
=
;σ[X]
=
![]() ;9.8.
a =
;9.8.
a = ![]() ;М[X]
= 2; D[X] =
;М[X]
= 2; D[X] =
![]() ;σ[X]
=
;σ[X]
=
![]() ;Р{Х ≤ 3}
=
;Р{Х ≤ 3}
=
![]() ;
Р{2 <Х< 5} =
;
Р{2 <Х< 5} = ![]() ;
Р{Х > 3,5}
=
;
Р{Х > 3,5}
=
![]() ;
;
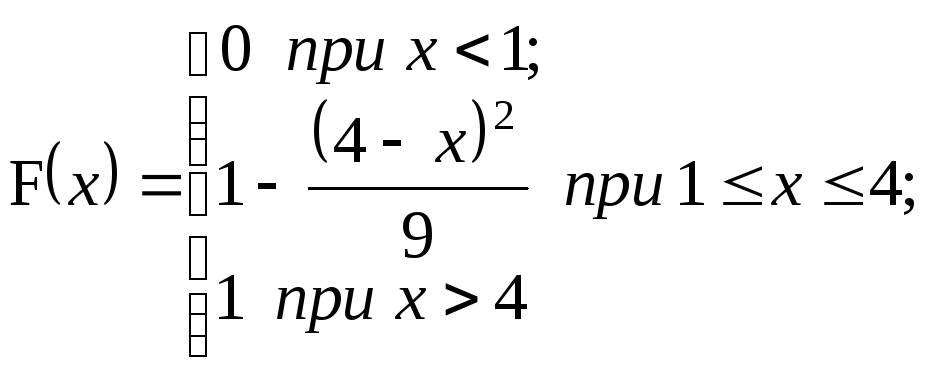 9.9.
9.9.
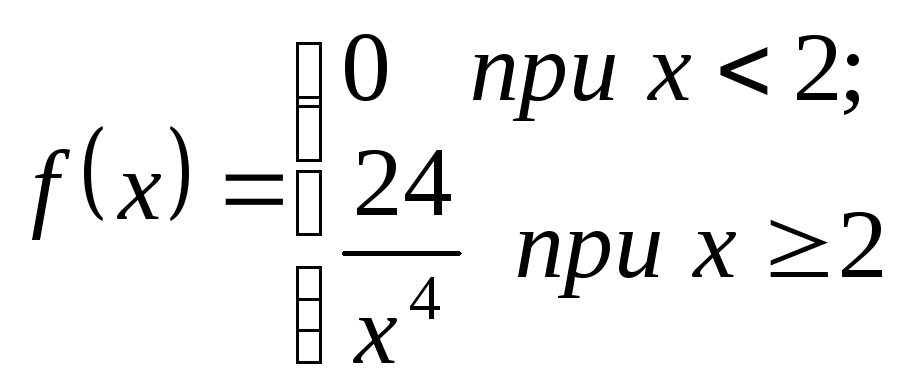 ;М[X]
= 2; D[X] = 8; σ[X]
=
;М[X]
= 2; D[X] = 8; σ[X]
=
![]() ;9.10.
а = 3;
;9.10.
а = 3;
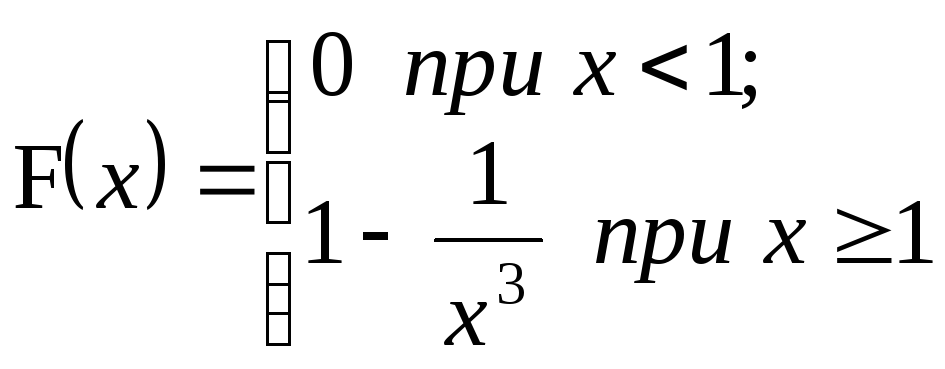 ;
P{2 < X < 4} =
;
P{2 < X < 4} =![]() ;Р{–2 < Х< 2} =
;Р{–2 < Х< 2} = ![]() ;
9.11.
;
9.11.
![]() ;
;![]() ;
;![]() .
.
§10 Биномиальное распределение
10.1. 0,625; 10.2. M[X] = 2; D[X] = 1,9;
-
10.3.
x
0
1
2
3
4
p
0,6561
0,2916
0,0486
0,0036
0,0001
M[X]
= 0,4; D[X] = 0,36; [X]
= 0,6; 10.4.
D[X] = 0,495; 10.5.
M[X] = 800; D[X] = 160; [X]
=
![]()
12,65; 10.6.
n
= 144; p
=
0,5;
12,65; 10.6.
n
= 144; p
=
0,5;
10.7.
-
10.8
x
0
1
2
3
P
0,008
0,096
0,384
0,512
M[X]
= 2,4; D[X] = 0,48; [X]
=
![]()
0,693.
0,693.
§11. Пуассоновское распределение
11.1.
0,375; 11.2.
![]() ;
;![]() 11.3.
=2;
P{X
> 0} = 1e2
0,865; 11.4.
а) 0,135;
б) 0,336;
11.5.
а) 0,15;
б) 0,575;
11.6.
0,135; 11.7.
M[X]
= 60; D[X]
= 60; [X]
=
11.3.
=2;
P{X
> 0} = 1e2
0,865; 11.4.
а) 0,135;
б) 0,336;
11.5.
а) 0,15;
б) 0,575;
11.6.
0,135; 11.7.
M[X]
= 60; D[X]
= 60; [X]
=
![]()
7,75; 11.8.
а) 0,225;
б) 0,2;
в) 0,575;
г) 0,95;
11.9.
0,8.
7,75; 11.8.
а) 0,225;
б) 0,2;
в) 0,575;
г) 0,95;
11.9.
0,8.
§12. Равномерное распределение
12.1.
M[X]
= 5; D[X]
= 3; [X]
=
![]()
1,73; 12.2.
0,6; 2,5 мин.; 12.3. P{X > 0,02}
= 0,3; P(
1,73; 12.2.
0,6; 2,5 мин.; 12.3. P{X > 0,02}
= 0,3; P(![]() > 0,02)
= 0,6; 12.4.
> 0,02)
= 0,6; 12.4.
![]() ;
12.5.
а) 0,7;
б) 0,25; 12.6.
0,4.
;
12.5.
а) 0,7;
б) 0,25; 12.6.
0,4.
§13. Показательное распределение
13.1.
а) M[T]
= 0,2; D[T]
= 0,04, [T]
= 0,2; б) M[T]
= 10; D[T]
= 100, [T] = 10;
13.2.
0,117; 0,632; 13.3.
а) 0.918; б) 0,471; 13.4.
0,135; 13.5.
0,233; 13.6. a) 0,029;
б) 0,657; в)0,314; г)0,343; 13.7.
![]() ;
13.8.
0,865; 13.9.
a) 0,950;
б) 0,050.
;
13.8.
0,865; 13.9.
a) 0,950;
б) 0,050.
§14. Нормальное распределение
14.1.
а) M[Х]
= –5; D[Х]
= 9, [Х]
= 3; б) M[Х]
= 1; D[Х]
= 16, [Х]
= 4; 14.2. f4, 2 (x)=![]() ;
P{1 X
5} = 0,6247; P{X
5} = 0,6915; 14.3.
0,2358; 14.4.
=
10; 14.5.
a
= 8,
= 5; 14.6.
0,9864; 14.7.
0,9876; 14.8. 0,31082
= 0,0966; 14.9.
a)
1,24%; б) 13,58%; 14.10.
12 мм;
0,9544; 14.11.
0,00135; 14.12.
0,7588; 14.13.
=4; 0,3085; 14.14.
a)
0,8533; б) 0,9736; 14.15.
0,8533; 14.16.
0,9868.
;
P{1 X
5} = 0,6247; P{X
5} = 0,6915; 14.3.
0,2358; 14.4.
=
10; 14.5.
a
= 8,
= 5; 14.6.
0,9864; 14.7.
0,9876; 14.8. 0,31082
= 0,0966; 14.9.
a)
1,24%; б) 13,58%; 14.10.
12 мм;
0,9544; 14.11.
0,00135; 14.12.
0,7588; 14.13.
=4; 0,3085; 14.14.
a)
0,8533; б) 0,9736; 14.15.
0,8533; 14.16.
0,9868.
§15. Теоремы группы ЦПТ
15.1. 0,8413; 15.2. 0,00087; 15.3. а) 0,0605; б) 0,8185; в) 0,0062; 15.4. 0,9708; 0,000011; 0,0720; 15.5. 0,9192; 15.6. 0,8413; 15.7. а) 0,0579; б) 0,0019; 15.8. а) 0,4887; б) 0,5; в) 0,5.
§16. Двумерные случайные величины
-
16.1
Х
2
3
9
У
0,2
0,8
P
0,26
0,38
0,36
Р
0,56
0,44
|
Х у = 0,2 |
2 |
3 |
9 |
|
У х = 3 |
0,2 |
0,8 |
|
Р |
0,321 |
0,393 |
0,286 |
|
Р |
0,579 |
0,421 |
16.2. M[Х] = 0,69; M[X2] = 0,867; D[Х] = 0,3909, [Х] = 0,6252; M[У] = 1,5; M[Y2] = 2,5; D[Y] = 0,25, [Y] = 0,5; M[XY] = 1,07; Kxy = 0,035; rxy = 0,11196; 16.3. M[Х] = 1,4; M[X2] = 2,38; D[Х] = 0,42, [Х] = 0,648; M[У] = 0,6; M[Y2]= 0,78; D[Y] = 0,42, [Y] = 0,648; M[XY] = 0,42; Kxy= –0,42; rxy= –1; зависимы;
|
X У |
0 |
1 |
2 |
|
0 |
0 |
0 |
0,49 |
|
1 |
0 |
0,42 |
0 |
|
2 |
0,09 |
0 |
0 |
16.4.
f(x)
=
2(1 – x)
при
0 x 1;
M[Х]
=
![]() ;
M[X2] =
;
M[X2] = ![]() ;D[Х] =
;D[Х] = ![]() ,
[Х] =
,
[Х] = ![]() ;
f(y) = 2(1 – y)
при
0 y 1;
M[У]
=
;
f(y) = 2(1 – y)
при
0 y 1;
M[У]
=
![]() ;
M[Y2]
=
;
M[Y2]
=
![]() ;
D[Y]
=
;
D[Y]
=
![]() ,
[Y] =
,
[Y] = ![]() ;
M[XY]
=
;
M[XY]
=
![]() ;
Kxy = –
;
Kxy = –![]() ;
rxy = –
;
rxy = –![]() ;
F(x;y) = 2(1 – x)(1 – y)
при
(х;у)
D;
16.5.
а = 4;
f(x) = 2x
при x[0;1],
f(y) = 2y
при
y[0;1];
f(xy) = 4xy = 2x2y = f(x)f(y)
X
и Y
независимы
Kxy =
rxy = 0,
f(yx) = 2y,
y[0;1],
f(xy) = 2x,
x[0;1],
;
F(x;y) = 2(1 – x)(1 – y)
при
(х;у)
D;
16.5.
а = 4;
f(x) = 2x
при x[0;1],
f(y) = 2y
при
y[0;1];
f(xy) = 4xy = 2x2y = f(x)f(y)
X
и Y
независимы
Kxy =
rxy = 0,
f(yx) = 2y,
y[0;1],
f(xy) = 2x,
x[0;1],
16.6.
f(x) = ![]() ,
x[–5;5];
M[Х]
= 0; [Х]
= 2,5; f(y) =
,
x[–5;5];
M[Х]
= 0; [Х]
= 2,5; f(y) = ![]() ,
y[–5;5];
M[Y]=0,
[Y]=2,5;
M[XY]=0;
Kxy= rxy=0;
f(x)f(y) =
,
y[–5;5];
M[Y]=0,
[Y]=2,5;
M[XY]=0;
Kxy= rxy=0;
f(x)f(y) = ![]()
![]() = f(x;
y)
X
и Y
– зависимы;
= f(x;
y)
X
и Y
– зависимы;
16.7.
f(xy)
=
![]() ;
16.8.
M[Х]
= 0,17; M[X2]
= 0,079; D[Х]
= 0,0501, [Х]
= 0,2238; M[У]
= 1,45; M[Y2]
= 2,275; D[Y]
= 0,1725, [Y]
= 0,4153; M[XY] = 0,28;
Kxy =
0,0335; rxy = 0,3604;
yx = 0,6687x + 1,3363;
xy=0,1942y – 0,1116;
16.9.
M[Х]
= 0,5; M[X2]
= 0,4; D[Х]
= 0,15, [Х]
= 0,3873; M[У]
= 0,75; M[Y2] = 0,625;
D[Y]
= 0,0625, [Y]
= 0,25; M[XY]
= 0,375; Kxy
=
0; 16.10.
f(x) = 2x,
x[0;1],
f(y)
= 0,5y,
y[0;1]
, f(xy)= xy = 2x0,5y = f(x)f(y)
X
и Y
независимы
Kxy =
rxy=0,
f(x;y) = 0,25x2y2,
(x;y)D;
16.11.
fx(x) = 0,5(sinx + cosx),
x
;
16.8.
M[Х]
= 0,17; M[X2]
= 0,079; D[Х]
= 0,0501, [Х]
= 0,2238; M[У]
= 1,45; M[Y2]
= 2,275; D[Y]
= 0,1725, [Y]
= 0,4153; M[XY] = 0,28;
Kxy =
0,0335; rxy = 0,3604;
yx = 0,6687x + 1,3363;
xy=0,1942y – 0,1116;
16.9.
M[Х]
= 0,5; M[X2]
= 0,4; D[Х]
= 0,15, [Х]
= 0,3873; M[У]
= 0,75; M[Y2] = 0,625;
D[Y]
= 0,0625, [Y]
= 0,25; M[XY]
= 0,375; Kxy
=
0; 16.10.
f(x) = 2x,
x[0;1],
f(y)
= 0,5y,
y[0;1]
, f(xy)= xy = 2x0,5y = f(x)f(y)
X
и Y
независимы
Kxy =
rxy=0,
f(x;y) = 0,25x2y2,
(x;y)D;
16.11.
fx(x) = 0,5(sinx + cosx),
x![]() ,
fy(y) = 0,5(siny + cosy),
y
,
fy(y) = 0,5(siny + cosy),
y![]() ,
M[Х]
= M[Y]
=
,
M[Х]
= M[Y]
=
![]() ;
M[X2]
= M[Y2]
=
;
M[X2]
= M[Y2]
=
![]() ;
D[X]
= D[Y]
=
;
D[X]
= D[Y]
=
![]() ;
[X]
= [Y]
0,4332; M[XY]
=
;
[X]
= [Y]
0,4332; M[XY]
=
![]() ;
Kxy =
;
Kxy =
![]()
0,0461; rxy
–0,2455; x
и y
– зависимы;
0,0461; rxy
–0,2455; x
и y
– зависимы;
![]() ,
(x,y)D;
,
(x,y)D;
![]() ,
(x,y)D;
16.12.
f(x,y)
= abе – (ах+bх) ;
16.13.
M[Х]
= 1,4; M[X2] = 2,15;
D[Х]
= 0,19, [Х]
= 0,4359; M[У]
= 0,7; M[Y2]
= 1,1; D[Y]
= 0,61, [Y]
= 0,7810; M[XY]
= 1; Kxy
=
0,02; rxy
=
0,0587; yx
=
0,1053x + 0,5526;
xy = 0,0328y + 1,3770
(или y = 30,5x–42).
,
(x,y)D;
16.12.
f(x,y)
= abе – (ах+bх) ;
16.13.
M[Х]
= 1,4; M[X2] = 2,15;
D[Х]
= 0,19, [Х]
= 0,4359; M[У]
= 0,7; M[Y2]
= 1,1; D[Y]
= 0,61, [Y]
= 0,7810; M[XY]
= 1; Kxy
=
0,02; rxy
=
0,0587; yx
=
0,1053x + 0,5526;
xy = 0,0328y + 1,3770
(или y = 30,5x–42).
