
Конечные формулы для методички по физике №3 / Решения методички 3 (электричество) beta2
.docЭЛЕКТРИЧЕСТВО
ВНИМАНИЕ!
В задачах
![]() Ф/м
– электрическая постоянная, а
Ф/м
– электрическая постоянная, а
![]() если явно не указано другое значение
если явно не указано другое значение
![]() .
.
1-1.
Напряженность электрического поля
задается формулой: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
Используя теорему Гаусса в дифференциальной
форме, найдите объемную плотность заряда
в точке
.
Используя теорему Гаусса в дифференциальной
форме, найдите объемную плотность заряда
в точке
![]() .
.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
(Кл/м^3)
.
(Кл/м^3)
1-2.
Напряженность электрического поля
задается формулой: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() .
Используя теорему Гаусса в дифференциальной
форме, найдите объемную плотность заряда
в точке
.
Используя теорему Гаусса в дифференциальной
форме, найдите объемную плотность заряда
в точке
![]() .
.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() .
(Кл/м^3)
.
(Кл/м^3)
1-3.
Напряженность электрического поля
задается формулой: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
Используя теорему Гаусса в дифференциальной
форме, найдите объемную плотность заряда
в точке
.
Используя теорему Гаусса в дифференциальной
форме, найдите объемную плотность заряда
в точке
![]() .
.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
(Кл/м^3)
.
(Кл/м^3)
ВНИМАНИЕ:
синус и косинус считать в радианах
(RAD)!!!
В стандартном виде числа округлять до
1 знака после запятой (например,
![]() ).
).
1-4.
Напряженность электрического поля
задается формулой
![]() .
Используя теорему Гаусса в дифференциальной
форме, найдите объемную плотность заряда
в точке
.
Используя теорему Гаусса в дифференциальной
форме, найдите объемную плотность заряда
в точке
![]() .
.
![]() .
(Кл/м^3)
.
(Кл/м^3)
1-5.
Напряженность электрического поля
задается формулой: а)
![]() ;
б)
;
б)
![]() .
Используя теорему Гаусса в дифференциальной
форме, найдите объемную плотность заряда
в точке
.
Используя теорему Гаусса в дифференциальной
форме, найдите объемную плотность заряда
в точке
![]() .
.
а)
![]() ;
б)
;
б)
![]() .
(Кл/м^3)
.
(Кл/м^3)
2-1.
Потенциал электростатического поля
зависит от координат по закону: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
Найти величину напряженности электрического
поля в точке
.
Найти величину напряженности электрического
поля в точке
![]() .
.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
(В/м)
.
(В/м)
2-2.
Потенциал электростатического поля
зависит от координат по закону: а)
![]() ;
б)
;
б)
![]() .
Найти величину напряженности электрического
поля в точке
.
Найти величину напряженности электрического
поля в точке
![]() .
.
а)
![]() ;
б)
;
б)
![]() .
(В/м)
.
(В/м)
2-3.
Потенциал электростатического поля
зависит от координат по закону: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
Найти величину напряженности электрического
поля в точке
.
Найти величину напряженности электрического
поля в точке
![]() .
.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() .
(В/м)
.
(В/м)
ВНИМАНИЕ: синус и косинус считать в радианах (RAD)!!!
ВНИМАНИЕ!
В задачах принять
![]() .
.
3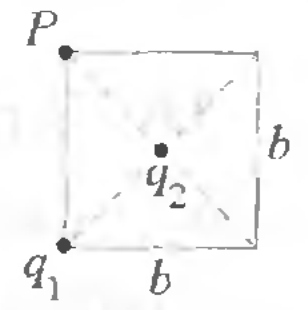 -1.
Заряд
-1.
Заряд
![]() находится в вершине квадрата со стороной
находится в вершине квадрата со стороной
![]() ,
а заряд
,
а заряд
![]() - в центре. Найти модуль напряженности
электрического поля в точке
- в центре. Найти модуль напряженности
электрического поля в точке
![]() ,
находящейся В ДРУГОЙ ВЕРШИНЕ этого
квадрата.
,
находящейся В ДРУГОЙ ВЕРШИНЕ этого
квадрата.
Ответ:
![]() .
Ответ дать в кВ/м (1Кв=1000В). В расчетах
мкКл переводить в Кл (1 Кл=10^6 мкКл).
.
Ответ дать в кВ/м (1Кв=1000В). В расчетах
мкКл переводить в Кл (1 Кл=10^6 мкКл).
3 -2.
Заряды
-2.
Заряды
![]() и
и
![]() находятся в соседних вершинах квадрата
со стороной
находятся в соседних вершинах квадрата
со стороной
![]() .
Найти модуль напряженности электрического
поля в точке
.
Найти модуль напряженности электрического
поля в точке
![]() ,
находящейся В ЦЕНТРЕ квадрата.
,
находящейся В ЦЕНТРЕ квадрата.
Ответ:
![]() .
Ответ дать в кВ/м (1Кв=1000В). В расчетах
мкКл переводить в Кл (1 Кл=10^6 мкКл).
.
Ответ дать в кВ/м (1Кв=1000В). В расчетах
мкКл переводить в Кл (1 Кл=10^6 мкКл).
3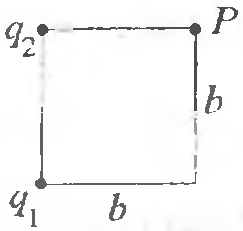 -3.
Заряды
-3.
Заряды
![]() и
и
![]() находятся в соседних вершинах квадрата
со стороной
находятся в соседних вершинах квадрата
со стороной
![]() .
Найти величину горизонтальной проекции
напряженности электрического поля в
точке
.
Найти величину горизонтальной проекции
напряженности электрического поля в
точке
![]() ,
находящейся В ТРЕТЬЕЙ ВЕРШИНЕ квадрата.
,
находящейся В ТРЕТЬЕЙ ВЕРШИНЕ квадрата.
Ответ:
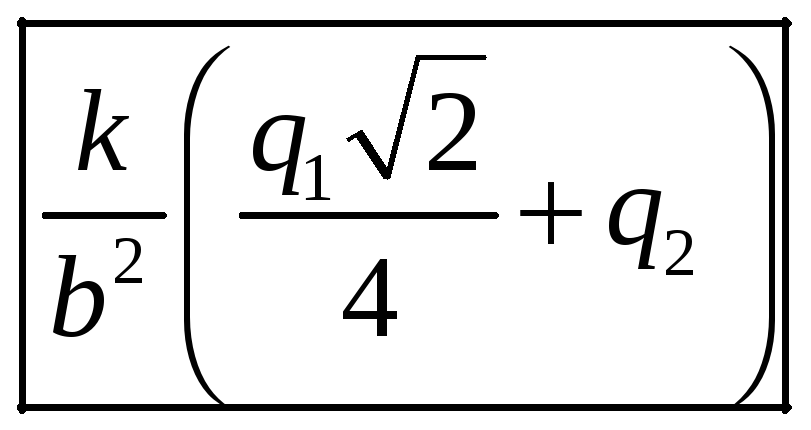 .
Ответ дать в кВ/м (1Кв=1000В). В расчетах
мкКл переводить в Кл (1 Кл=10^6 мкКл).
.
Ответ дать в кВ/м (1Кв=1000В). В расчетах
мкКл переводить в Кл (1 Кл=10^6 мкКл).
3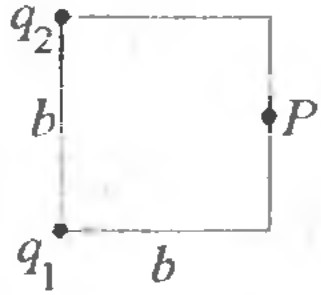 -4.
Заряды
-4.
Заряды
![]() и
и
![]() находятся в соседних вершинах квадрата
со стороной
находятся в соседних вершинах квадрата
со стороной
![]() .
Найти величину горизонтальной проекции
напряженности электрического поля в
точке
.
Найти величину горизонтальной проекции
напряженности электрического поля в
точке
![]() ,
находящейся НА СЕРЕДИНЕ ПРОТИВОПОЛОЖН
ОЙ СТОРОНЫ квадрата.
,
находящейся НА СЕРЕДИНЕ ПРОТИВОПОЛОЖН
ОЙ СТОРОНЫ квадрата.
Ответ:
 .
Ответ дать в кВ/м (1Кв=1000В). В расчетах
мкКл переводить в Кл (1 Кл=10^6 мкКл).
.
Ответ дать в кВ/м (1Кв=1000В). В расчетах
мкКл переводить в Кл (1 Кл=10^6 мкКл).
3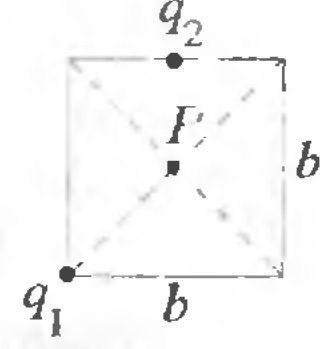 -5.
Заряд
-5.
Заряд
![]() находится в вершине квадрата со стороной
находится в вершине квадрата со стороной
![]() ,
а заряд
,
а заряд
![]() - на середине стороны. Найти МОДУЛЬ
НАПРЯЖЕННОСТИ электрического поля в
точке
- на середине стороны. Найти МОДУЛЬ
НАПРЯЖЕННОСТИ электрического поля в
точке
![]() ,
находящейся в центре квадрата.
,
находящейся в центре квадрата.
Ответ:
![]() .
Ответ дать в кВ/м (1Кв=1000В). В расчетах
мкКл переводить в Кл (1 Кл=10^6 мкКл).
.
Ответ дать в кВ/м (1Кв=1000В). В расчетах
мкКл переводить в Кл (1 Кл=10^6 мкКл).
3 -6.
Заряд
-6.
Заряд
![]() находится в вершине квадрата со стороной
находится в вершине квадрата со стороной
![]() ,
а заряд
,
а заряд
![]() - на середине стороны. Найти ВЕЛИЧИНУ
ВЕРТИКАЛЬНОЙ ПРОЕКЦИИ НАПРЯЖЕННОСТИ
электрического поля в точке
- на середине стороны. Найти ВЕЛИЧИНУ
ВЕРТИКАЛЬНОЙ ПРОЕКЦИИ НАПРЯЖЕННОСТИ
электрического поля в точке
![]() ,
находящейся в центре квадрата.
,
находящейся в центре квадрата.
Ответ:
 .
Ответ дать в кВ/м (1Кв=1000В). В расчетах
мкКл переводить в Кл (1 Кл=10^6 мкКл).
.
Ответ дать в кВ/м (1Кв=1000В). В расчетах
мкКл переводить в Кл (1 Кл=10^6 мкКл).
ВНИМАНИЕ!!!
В задачах принять
![]() .
.
4 -1.
Заряд
-1.
Заряд
![]() находится в вершине квадрата со стороной
находится в вершине квадрата со стороной
![]() ,
а заряд
,
а заряд
![]() - в центре. Найти потенциал электрического
поля в точке
- в центре. Найти потенциал электрического
поля в точке
![]() ,
находящейся в другой вершине этого
квадрата.
,
находящейся в другой вершине этого
квадрата.
О твет:
твет:
![]() .
Ответ дать в кВ (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
.
Ответ дать в кВ (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
4-2.
Заряды
![]() и
и
![]() находятся в соседних вершинах квадрата
со стороной
находятся в соседних вершинах квадрата
со стороной
![]() .
Найти потенциал электрического поля в
точке
.
Найти потенциал электрического поля в
точке
![]() ,
ДЕЛЯЩЕЙ сторону квадрата на два равных
отрезка.
,
ДЕЛЯЩЕЙ сторону квадрата на два равных
отрезка.
Ответ:
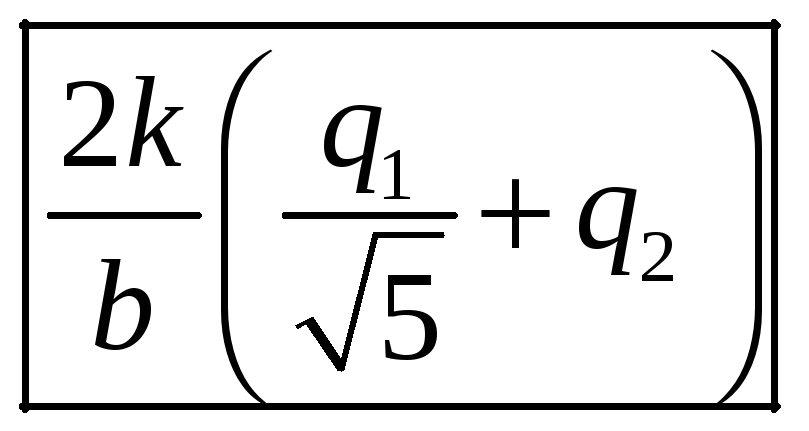 .
Ответ дать в кВ (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
.
Ответ дать в кВ (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
4 -3.
Заряды
-3.
Заряды
![]() и
и
![]() находятся в соседних вершинах квадрата
со стороной
находятся в соседних вершинах квадрата
со стороной
![]() .
Найти потенциал электрического поля в
точке
.
Найти потенциал электрического поля в
точке
![]() ,
НАХОДЯЩЕЙСЯ НА СЕРЕДИНЕ ПРОТИВОПОЛОЖНОЙ
стороны квадрата.
,
НАХОДЯЩЕЙСЯ НА СЕРЕДИНЕ ПРОТИВОПОЛОЖНОЙ
стороны квадрата.
Ответ:
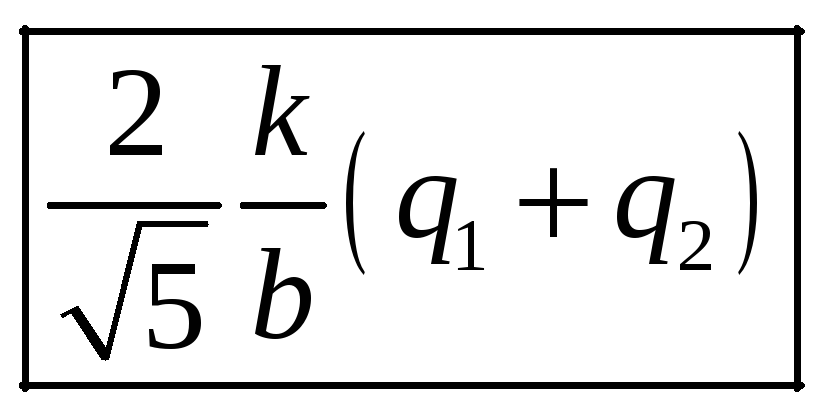 .
Ответ дать в кВ (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
.
Ответ дать в кВ (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
4 -4.
Заряд
-4.
Заряд
![]() находится в вершине квадрата со стороной
находится в вершине квадрата со стороной
![]() ,
а заряд
,
а заряд
![]() - на середине стороны. Найти потенциал
электрического поля в точке
- на середине стороны. Найти потенциал
электрического поля в точке
![]() ,
находящейся на середине ПРОТИВОПОЛОЖНОЙ
стороны квадрата.
,
находящейся на середине ПРОТИВОПОЛОЖНОЙ
стороны квадрата.
Ответ:
 .
Ответ дать в кВ (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
.
Ответ дать в кВ (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
4 -5.
Заряд
-5.
Заряд
![]() находится в вершине квадрата со стороной
находится в вершине квадрата со стороной
![]() ,
а заряд
,
а заряд
![]() - на середине стороны. Найти потенциал
электрического поля в точке
- на середине стороны. Найти потенциал
электрического поля в точке
![]() ,
находящейся на середине стороны квадрата.
,
находящейся на середине стороны квадрата.
Ответ:
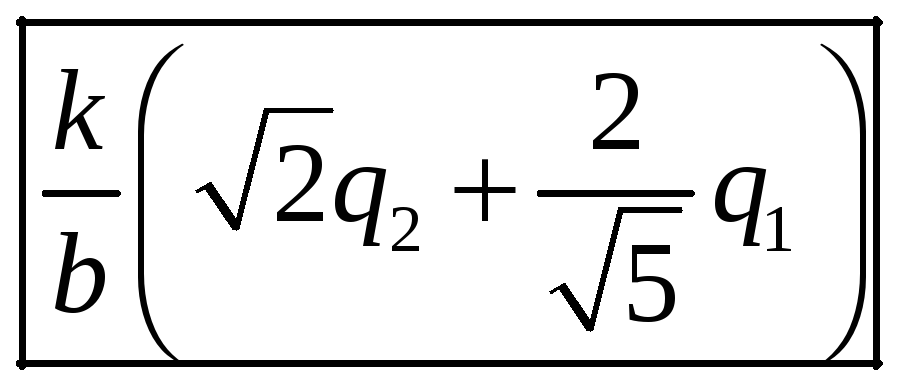 .
Ответ дать в кВ (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
.
Ответ дать в кВ (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
4 -6.
Заряд
-6.
Заряд
![]() находится в вершине квадрата со стороной
находится в вершине квадрата со стороной
![]() ,
а заряд
,
а заряд
![]() - на середине стороны. Найти потенциал
электрического поля в точке
- на середине стороны. Найти потенциал
электрического поля в точке
![]() ,
находящейся В ПРОТИВОПОЛОЖНОЙ ВЕРШИНЕ
квадрата.
,
находящейся В ПРОТИВОПОЛОЖНОЙ ВЕРШИНЕ
квадрата.
Ответ:
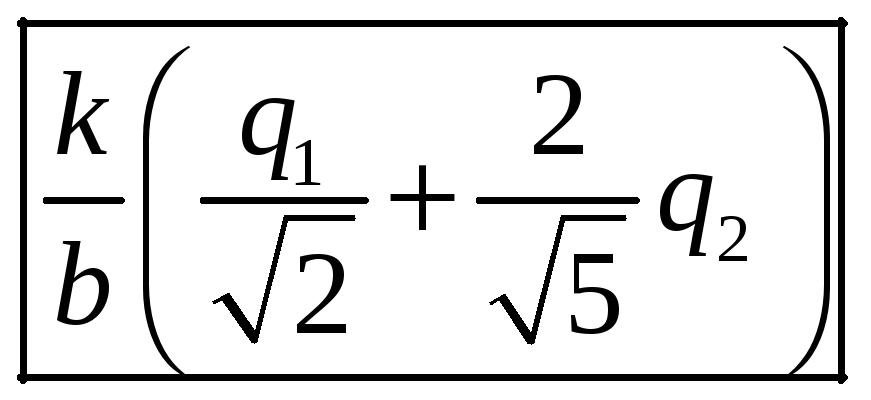 .
Ответ дать в кВ (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
.
Ответ дать в кВ (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
5![]() -1.
Вдоль стержня длины
-1.
Вдоль стержня длины
![]() равномерно распределен заряд
равномерно распределен заряд
![]() .
Найти потенциал в точке
.
Найти потенциал в точке
![]() на продолжении стержня на расстоянии
на продолжении стержня на расстоянии
![]() от его конца.
от его конца.
Ответ:
![]() .
Ответ дать в кВ (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
.
Ответ дать в кВ (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
5![]() -2.
Вдоль стержня длины
-2.
Вдоль стержня длины
![]() равномерно распределен заряд с линейной
плотностью
равномерно распределен заряд с линейной
плотностью
![]() .
Найти потенциал в точке
.
Найти потенциал в точке
![]() на продолжении стержня на расстоянии
на продолжении стержня на расстоянии
![]() от его конца.
от его конца.
О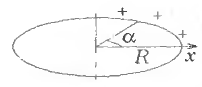 твет:
твет:
![]() .
Ответ дать в кВ (1Кв=1000В). В расчетах
мкКл/м переводить в Кл/м (1 Кл=10^6 мкКл).
.
Ответ дать в кВ (1Кв=1000В). В расчетах
мкКл/м переводить в Кл/м (1 Кл=10^6 мкКл).
5-3.
Положительный заряд распределен по
тонкому кольцу радиуса
![]() с линейной плотностью
с линейной плотностью
![]() ,
,
![]() .
Определить потенциал, создаваемый этим
зарядом в центре кольца.
.
Определить потенциал, создаваемый этим
зарядом в центре кольца.
Ответ:
![]() .
Ответ дать в кВ (1Кв=1000В). В расчетах
мкКл/м переводить в Кл/м (1 Кл=10^6 мкКл).
Считать
.
Ответ дать в кВ (1Кв=1000В). В расчетах
мкКл/м переводить в Кл/м (1 Кл=10^6 мкКл).
Считать
![]() .
.
5 -4.
Положительный заряд распределен по
тонкому кольцу радиуса
-4.
Положительный заряд распределен по
тонкому кольцу радиуса
![]() с линейной плотностью
с линейной плотностью
![]() ,
,
![]() .
Определить потенциал, создаваемый этим
зарядом в центре кольца.
.
Определить потенциал, создаваемый этим
зарядом в центре кольца.
Ответ:
![]() .
Ответ дать в кВ (1Кв=1000В). В расчетах
мкКл/м переводить в Кл/м (1 Кл=10^6 мкКл).
Считать
.
Ответ дать в кВ (1Кв=1000В). В расчетах
мкКл/м переводить в Кл/м (1 Кл=10^6 мкКл).
Считать
![]() .
.
5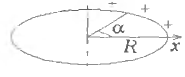 -5.
Положительный заряд распределен по
тонкому кольцу радиуса
-5.
Положительный заряд распределен по
тонкому кольцу радиуса
![]() с линейной плотностью
с линейной плотностью
![]() ,
,
![]() .
Определить потенциал, создаваемый этим
зарядом в центре кольца.
.
Определить потенциал, создаваемый этим
зарядом в центре кольца.
Ответ:
![]() .
Ответ дать в кВ (1Кв=1000В). В расчетах
мкКл/м переводить в Кл/м (1 Кл=10^6 мкКл).
Считать
.
Ответ дать в кВ (1Кв=1000В). В расчетах
мкКл/м переводить в Кл/м (1 Кл=10^6 мкКл).
Считать
![]() .
.
5![]() -6.
Тонкий стержень заряжен неравномерно.
Электрический заряд распределен по
нему с линейной плотностью
-6.
Тонкий стержень заряжен неравномерно.
Электрический заряд распределен по
нему с линейной плотностью
![]() ,
,
![]() ,
где
,
где
![]() - координата точки на стержне,
- координата точки на стержне,
![]() - длина стержня. Чему равна величина
потенциала, создаваемого этим зарядом
в начале координат
- длина стержня. Чему равна величина
потенциала, создаваемого этим зарядом
в начале координат
![]() ,
совпадающем с концом стержня?
,
совпадающем с концом стержня?
Ответ:
![]() .
Ответ дать в кВ (1Кв=1000В). В расчетах
мкКл/м переводить в Кл/м (1 Кл=10^6 мкКл).
.
Ответ дать в кВ (1Кв=1000В). В расчетах
мкКл/м переводить в Кл/м (1 Кл=10^6 мкКл).
5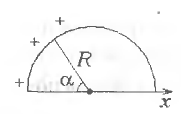 -7.
Положительный заряд распределен по
тонкому полукольцу радиуса
-7.
Положительный заряд распределен по
тонкому полукольцу радиуса
![]() с линейной плотностью
с линейной плотностью
![]() ,
,
![]() .
Определить потенциал, создаваемый этим
зарядом в центре полукольца.
.
Определить потенциал, создаваемый этим
зарядом в центре полукольца.
Ответ:
![]() .
Ответ дать в кВ (1Кв=1000В). В расчетах
мкКл/м переводить в Кл/м (1 Кл=10^6 мкКл).
Считать
.
Ответ дать в кВ (1Кв=1000В). В расчетах
мкКл/м переводить в Кл/м (1 Кл=10^6 мкКл).
Считать
![]() .
.
5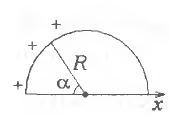 -8.
Положительный заряд распределен по
тонкому полукольцу радиуса
-8.
Положительный заряд распределен по
тонкому полукольцу радиуса
![]() с линейной плотностью
с линейной плотностью
![]() ,
,
![]() .
Определить потенциал, создаваемый этим
зарядом в центре полукольца.
.
Определить потенциал, создаваемый этим
зарядом в центре полукольца.
Ответ:
![]() .
Ответ дать в кВ (1Кв=1000В). В расчетах
мкКл/м переводить в Кл/м (1 Кл=10^6 мкКл).
Считать
.
Ответ дать в кВ (1Кв=1000В). В расчетах
мкКл/м переводить в Кл/м (1 Кл=10^6 мкКл).
Считать
![]() .
.
6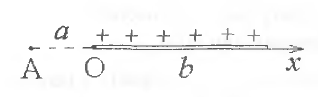 -1.
Вдоль стержня длины
-1.
Вдоль стержня длины
![]() равномерно распределен заряд
равномерно распределен заряд
![]() .
Найти величину напряженности электрического
поля в точке
.
Найти величину напряженности электрического
поля в точке
![]() на продолжении стержня на расстоянии
на продолжении стержня на расстоянии
![]() от
его конца.
от
его конца.
Ответ:
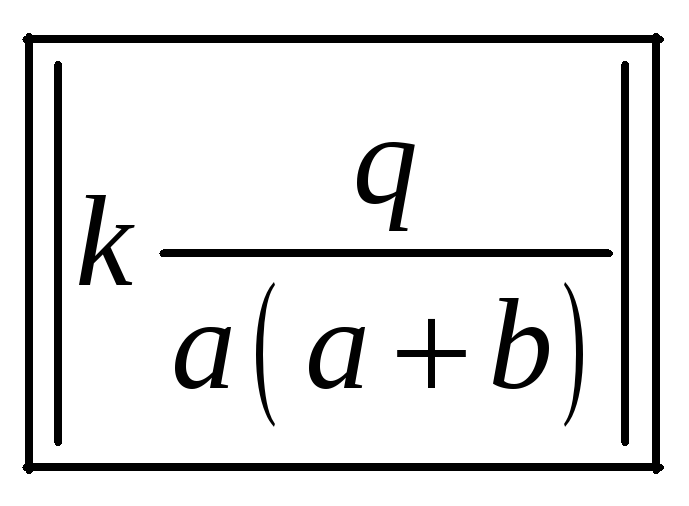 .
Ответ
дать в кВ/м (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
.
Ответ
дать в кВ/м (1Кв=1000В). В расчетах мкКл
переводить в Кл (1 Кл=10^6 мкКл).
6 -2.
Вдоль стержня длины
-2.
Вдоль стержня длины
![]() равномерно распределен заряд с линейной
плотностью
равномерно распределен заряд с линейной
плотностью
![]() .
Найти величину напряженности электрического
поля в точке
.
Найти величину напряженности электрического
поля в точке
![]() на продолжении стержня на расстоянии
на продолжении стержня на расстоянии
![]() от его конца.
от его конца.
Ответ:
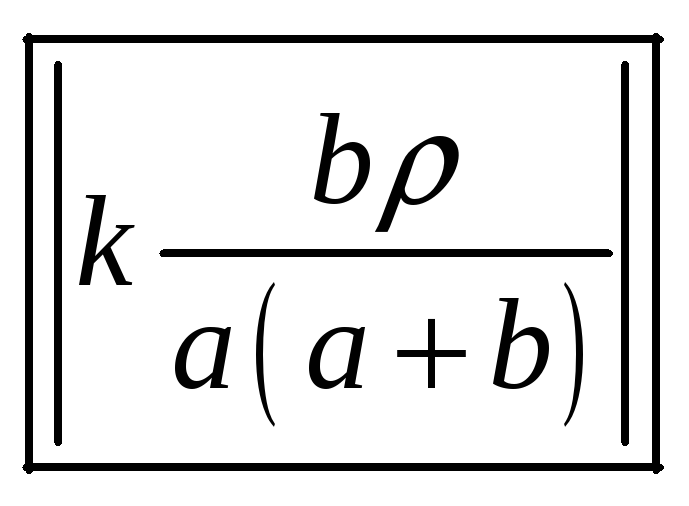 .
Ответ
дать в кВ/м (1Кв=1000В). В расчетах мкКл/м
переводить в Кл/м (1 Кл=10^6 мкКл).
.
Ответ
дать в кВ/м (1Кв=1000В). В расчетах мкКл/м
переводить в Кл/м (1 Кл=10^6 мкКл).
6 -3.
Заряд распределен по тонкому кольцу
радиуса
-3.
Заряд распределен по тонкому кольцу
радиуса
![]() с линейной плотностью
с линейной плотностью
 .
Определить величину проекции на ось
.
Определить величину проекции на ось
![]() напряженности электрического поля,
создаваемого этим зарядом в центре
кольца.
напряженности электрического поля,
создаваемого этим зарядом в центре
кольца.
Ответ:
![]() .
Ответ
дать в кВ/м (1Кв=1000В). В расчетах мкКл/м
переводить в Кл/м (1 Кл=10^6 мкКл).
.
Ответ
дать в кВ/м (1Кв=1000В). В расчетах мкКл/м
переводить в Кл/м (1 Кл=10^6 мкКл).
6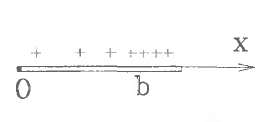 -4.
Тонкий стержень заряжен неравномерно.
Электрический заряд распределен по
нему с линейной плотностью
-4.
Тонкий стержень заряжен неравномерно.
Электрический заряд распределен по
нему с линейной плотностью
![]() ,
где
,
где
![]() – координата точки на стержне,
– координата точки на стержне,
![]() – длина стержня. Чему равна величина
напряженности электрического поля,
создаваемого этим зарядом в начале
координат
– длина стержня. Чему равна величина
напряженности электрического поля,
создаваемого этим зарядом в начале
координат
![]() ,
совпадающем с концом стержня? Ответ:
,
совпадающем с концом стержня? Ответ:
![]() .
(кВ/м)
.
(кВ/м)
6 -5.
Тонкий стержень заряжен неравномерно.
Электрический заряд распределен по
нему с линейной плотностью
-5.
Тонкий стержень заряжен неравномерно.
Электрический заряд распределен по
нему с линейной плотностью
![]() ,
где
,
где
![]() – координата точки на стержне,
– координата точки на стержне,
![]() – длина стержня. Чему равна величина
напряженности электрического поля,
создаваемого этим зарядом в начале
координат
– длина стержня. Чему равна величина
напряженности электрического поля,
создаваемого этим зарядом в начале
координат
![]() ,
совпадающем с концом стержня? Ответ:
,
совпадающем с концом стержня? Ответ:
![]() .
(кВ/м)
.
(кВ/м)
6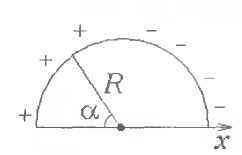 -6.
Заряд распределен по тонкому полукольцу
радиуса
-6.
Заряд распределен по тонкому полукольцу
радиуса
![]() с линейной плотностью
с линейной плотностью
 .
Определить проекцию на ось
.
Определить проекцию на ось
![]() напряженности электрического поля,
создаваемого этим зарядом в центре
полукольца.
напряженности электрического поля,
создаваемого этим зарядом в центре
полукольца.
Ответ:
![]() .
(кВ/м)
.
(кВ/м)
6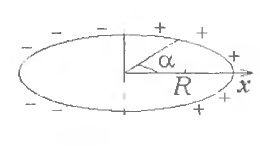 -7.
Заряд распределен по тонкому кольцу
радиуса
-7.
Заряд распределен по тонкому кольцу
радиуса
![]() с линейной плотностью
с линейной плотностью
 .
Определить величину проекции на ось
.
Определить величину проекции на ось
![]() напряженности электрического поля,
создаваемого этим зарядом в центре
кольца. Ответ:
напряженности электрического поля,
создаваемого этим зарядом в центре
кольца. Ответ:
![]() .
(кВ/м)
.
(кВ/м)
7-1.
По проводу сопротивлением
![]() течет переменный электрический ток.
Сила тока изменяется по закону.
а)
течет переменный электрический ток.
Сила тока изменяется по закону.
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() д)
д)
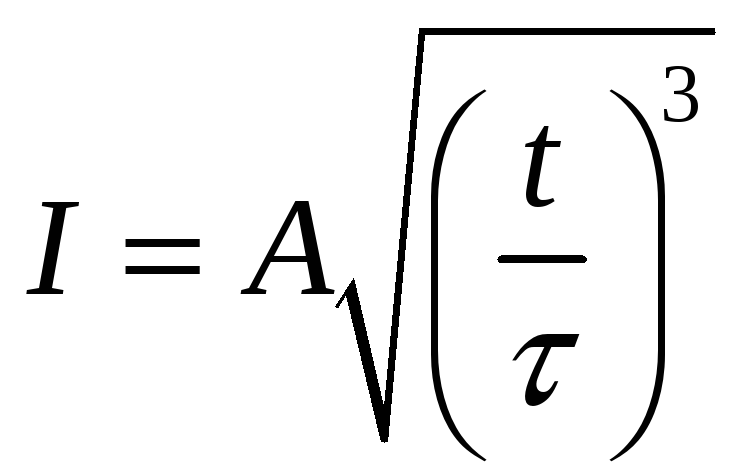 е)
е)
 ж)
ж)
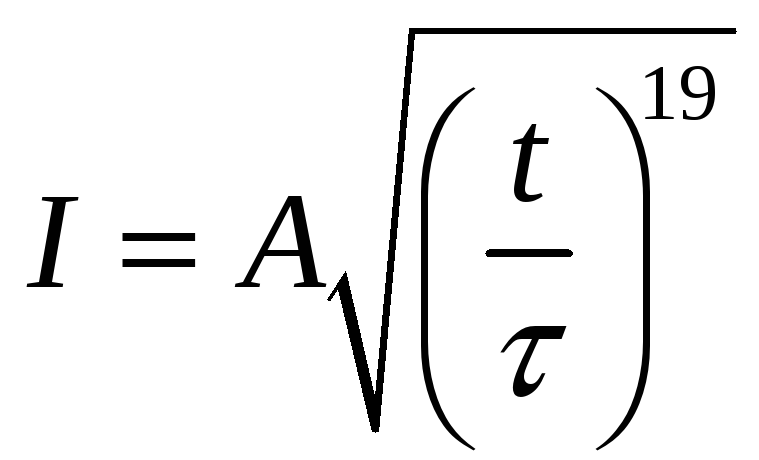 .
Чего найти – хрен знает, однако, наверное,
работу или какую-нибудь теплоту.
Короче,
общая формула для всех этих буковок
а)-ж) такова:
.
Чего найти – хрен знает, однако, наверное,
работу или какую-нибудь теплоту.
Короче,
общая формула для всех этих буковок
а)-ж) такова:
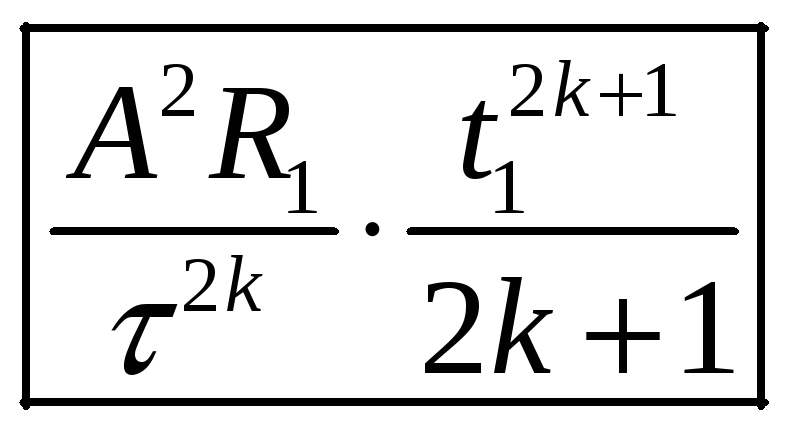 .
Здесь
.
Здесь
![]() - степень при
- степень при
![]() ,
например, для а)
,
например, для а)
![]() ,
для б)
,
для б)
![]() ,
а для ж)
,
а для ж)
![]() .
Ответ
давать в миллиджоулях (мДж), 1Дж=1000мДж.
(Чтобы из Джоулей получить мДж надо
Джоули умножить на 1000).
.
Ответ
давать в миллиджоулях (мДж), 1Дж=1000мДж.
(Чтобы из Джоулей получить мДж надо
Джоули умножить на 1000).
7-2.
По проводу сопротивлением
![]() течет переменный электрический ток.
Сила тока изменяется по закону. а)
течет переменный электрический ток.
Сила тока изменяется по закону. а)
![]() ;
б)
;
б)
![]() .
Чему равно количество теплоты, выделившейся
в проводе за время
.
Чему равно количество теплоты, выделившейся
в проводе за время
![]() ?
?
а)
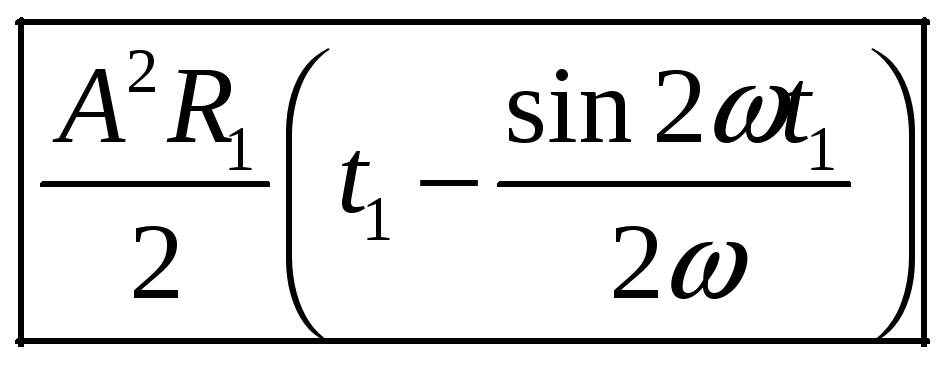 ;
б)
;
б)
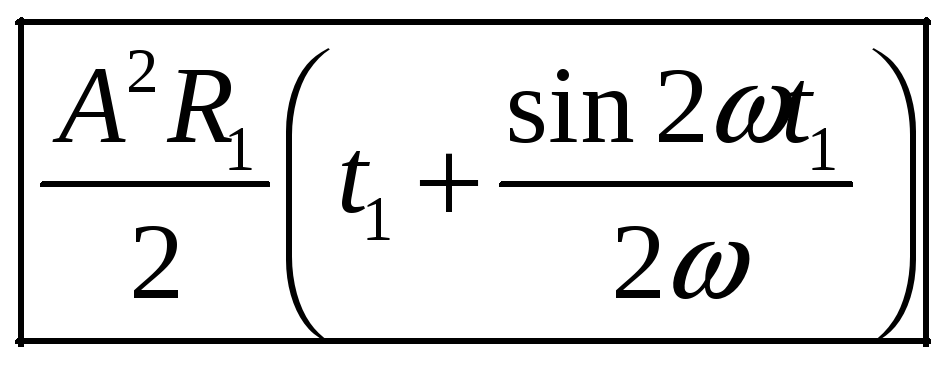 .
ВНИМАНИЕ!!!
Синус считать в градусах (DEG)!!!
Ответ давать в миллиджоулях (мДж),
1Дж=1000мДж. (Чтобы из Джоулей получить
мДж надо Джоули умножить на 1000).
.
ВНИМАНИЕ!!!
Синус считать в градусах (DEG)!!!
Ответ давать в миллиджоулях (мДж),
1Дж=1000мДж. (Чтобы из Джоулей получить
мДж надо Джоули умножить на 1000).
7-3.
По проводу сопротивлением
![]() течет переменный электрический ток.
Сила тока изменяется по закону
течет переменный электрический ток.
Сила тока изменяется по закону
![]() .
Чему равно количество теплоты, выделившейся
в проводе за время
.
Чему равно количество теплоты, выделившейся
в проводе за время
![]() ?
?
Ответ:
![]() .
Ответ давать в миллиджоулях (мДж),
1Дж=1000мДж. (Чтобы из Джоулей получить
мДж надо Джоули умножить на 1000).
.
Ответ давать в миллиджоулях (мДж),
1Дж=1000мДж. (Чтобы из Джоулей получить
мДж надо Джоули умножить на 1000).
