
- •Московский автомобильно-дорожный институт (государственный технический университет)
- •Материя и размеры наблюдаемой части Вселенной
- •4.Принцип относительности в механике.
- •Динамические параметры
- •Лекция 3. Законы сохранения. Уравнения движения. Динамика твердого тела.
- •Частные законы сохранения
- •Лекция 4. Фундаментальные и нефундаментальные взаимодействия
- •Реальные силы. Силы упругости и силы трения
- •Силы трения
- •Гармонические волны. Суперпозиция волн. Упругие и
- •Лекция 11. Тождественные частицы в классической и квантовой физике. Классическая и квантовая статистики
- •Термодинамика Земли, Марса и Венеры
- •Лекция 14. Энергетическая проблема и пути её решения
- •Мировые запасы минерального сырья
- •Используемые формулы
- •Закон сохранения момента импульса и закон динамики вращательного движения
- •Раздел механика
- •1. Кинематика
- •2. Момент инерции
- •3. Закон сохранения импульса и механической энергии
- •4. Закон сохранения момента импульса и закон динамики вращательного движения
- •Используемые формулы
- •6. Принцип суперпозиции магнитных полей
- •7. Закон Кулона. Напряженность электрических полей
- •8. Магнитная индукция. Сила Лоренца
- •Колебания
- •Сложение гармонических колебаний
- •Гармонические колебания
- •Контрольное задание №2 Волны
- •1. Уравнение волны
- •2. Эффект Доплера
- •3.Интенсивность и громкость звука
- •Стоячие волны
- •5.Интерференция волн
- •6.Дифракция волн
- •7. Квантовая физика. Туннельный эффект
- •Закон радиоактивного распада. Дефект массы атомного ядра
- •Квантовая теория атома водорода по модели Нильса Бора
- •Классическая статистика Больцмана и Максвелла
- •Контрольное задание №3
- •1. Закон динамики поступательного движения
- •2. Расчет момента инерции
- •3. Квантовое строение атома водорода
- •Квантовая теория полупроводников
- •Содержание
Лекция 11. Тождественные частицы в классической и квантовой физике. Классическая и квантовая статистики
Соотношения неопределенности Гайзенберга
хрh, где х - точность определения координаты микрочастицы, р- точность определения импульса микрочастицы.
2. Классические и квантовые тождественные частицы
|
Классическое описание
|
Квантовое описание |
|
Законы динамики mdv/dt=F dL/dt= rxF Е и р принимают лю- бые значения. Если задать исходные данные координат и скоростей частиц или тел, то можно рассчитать их траекторию с наперед заданной точностью.
В классической физике одинаковые частицы различаются, хотя бы своими координатами. |
Уравнение Шредингера =nlms . E,p,L,L2 - квантуются, т.е принимают строго определенные значения. Отсутствует понятие траектории отдельной частицы. 2 характеризует вероятность обнаружения частицы в той или иной области пространства. Реальные физические величины - статистические средние по большому ансамблю частиц. Квантовые частицы тождественны - принципиально неразличимы. Поскольку волновые пакеты, описывающие частицы могут перекрываться, то в одной и той же точке пространства возможно с какой-то вероятностью пребывание одновременно нескольких частиц. |
Физические
величины, характеризующие элементарные
частицы, атомы и молекулы (размеры,
масса, импульс, энергия и т.д.) настолько
малы, что в любом макроэксперименте мы
сталкиваемся с системами, состоящими
из огромного числа отдельных частиц.
Результаты измерений в таком эксперименте
оказываются статистически средними по
большому числу частиц. Понятие
статистического распределения вводят
для описания событий, носящих чисто
случайный характер. Вероятность появления
значения величины х, лежащего в интервале
от х до х+dx
для системы N
частиц можно представить dW=
dN/N=f(x)dx.
Здесь dN
– число частиц, имеющих значение х в
интервале от х до х+dx,
f(x)
– функция распределения. Вероятность
того, что значение величины х заключено
в интервале от 0 до ∞
равно 1, то есть W
=
![]() Тогда среднее значение величиныg(x)
определится следующим образом <g(x)>=
Тогда среднее значение величиныg(x)
определится следующим образом <g(x)>=![]() ,
например, <x>=
,
например, <x>=![]() ,
<x2>=
,
<x2>=![]()
3.Квантовые статистики
- Если при перестановке пары квантовых частиц в системе большого числа частиц описывающая их волновая функция не меняется, т.е. симметрична по отношению к операции перестановки двух частиц, то такие частицы называются бозонами, а система бозе-частиц описывается статистикой Бозе. Пример - газ фотонов - квантов электромагнитной энергии.
Функция распределения по энергиям Е для бозонов имеет вид:
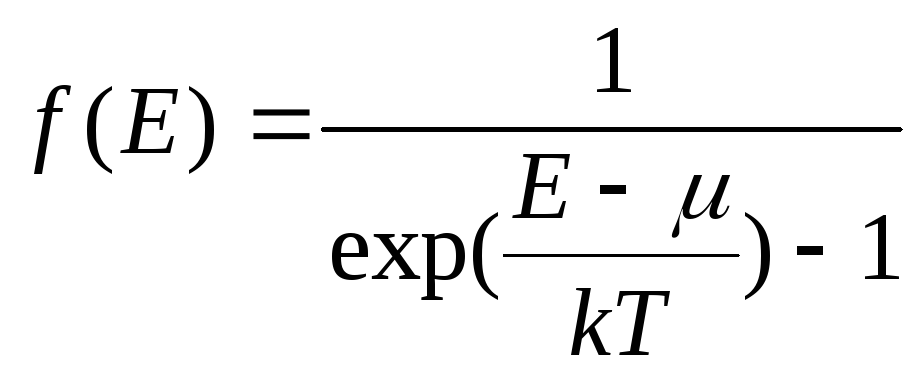 ,
где
- химический потенциал.
,
где
- химический потенциал.
- Если при перестановке пары частиц местами волновая функция меняет знак, т.е. оказывается несимметричной, то система таких тождественных частиц называется фермионами. Фермионы описываются статистикой Ферми-Дирака. Пример - газ электронов проводимости в металлах.
Функция распределения для фермионов по энергиям Е имеет вид:

f
 (E)
kT
(E)
kT


 1
1
 T=0
T0
f(E)=
T=0
T0
f(E)=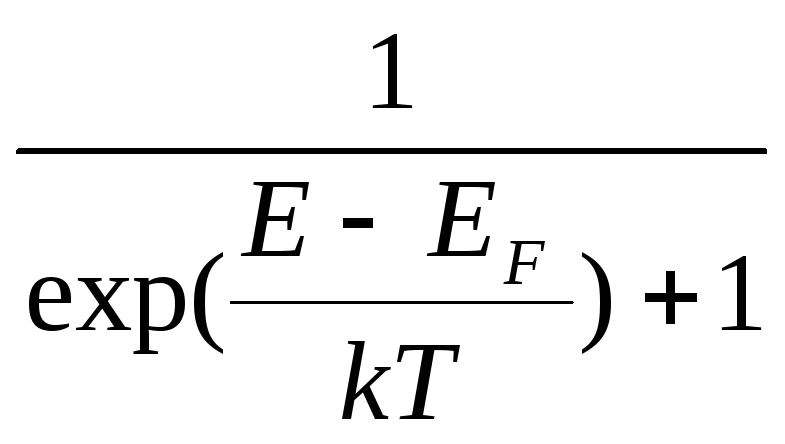 ,
,
 0
E
0
E
EF
где ЕF – энергия Ферми – максимальная энергия электронов проводимости при абсолютном нуле температур. Физический смысл 1 на графике функции распределения в том, что в каждом квантовом состоянии с энергией Е может находится только один электрон с данным набором квантовых чисел.
4.Распределения Максвелла – Больцмана
В
системе классических частиц – молекул
идеального газа функция распределения
f(v)=![]() =n/(nv)
молекул этого газа по скоростям называется
распределением Максвелла.
=n/(nv)
молекул этого газа по скоростям называется
распределением Максвелла.
n /(nv)
/(nv)





 v
v
vвер
Здесь vвер – наиболее вероятное значение скорости молекул идеального газа.
Средняя
скорость молекул идеального газа <v>=![]()
Средний
квадрат скорости <v2>=![]() .
Поэтому среднее значение кинетической
энергии молекулы идеального газа равно
.
Поэтому среднее значение кинетической
энергии молекулы идеального газа равно
<W>=<![]() >=
>=![]() .
.
Классическое распределение Больцмана числа частиц в единице объема по высоте z находится из распределения Больцмана
f(z)
=![]() .
Здесьno
– концентрация молекул газа вблизи
поверхности Земли ( z
= 0).
.
Здесьno
– концентрация молекул газа вблизи
поверхности Земли ( z
= 0).
Воспользуемся уравнением состояния идеального газа, из которого получим давление
![]() ,
тогда получим барометрическую формулу
( распределение давления газа в атмосфере
с высотой:
,
тогда получим барометрическую формулу
( распределение давления газа в атмосфере
с высотой:
![]() .
Здесь Ро
– давление в атмосфере вблизи поверхности
Земли.
.
Здесь Ро
– давление в атмосфере вблизи поверхности
Земли.
Контрольные вопросы
Различие понятия тождественных частиц в классической
и квантовой физике.
2. Принцип неопределенности и его физический смысл.
3.Что такое корпускулярно-волновой дуализм?
4. Физический смысл распределений Максвелла и Больцмана.
Литература
1. И.В.Савельев Курс общей физики т.3,гл.2-9,2-10,4,7-52,
Наука,М.,1977г.
2. Б.М.Яворский, А.А.Пинский Основы физики т.2,гл.68-70, Наука, М.,1974г.
3. Дж.Орир Физика т.2 гл.24,25 Мир,м.,1981г.
Лекция 12. Три начала термодинамики. Фазовые состояния вещества. Фазовые переходы. Жидкие кристаллы
Понятие о статистическом и термодинамическом методах
В основе статистического метода лежит метод Гиббса. Он возник как последовательное обобщение работ Клаузиуса, Максвелла и Больцмана по атомно-молекулярной теории тепла. Работы Гиббса печатались в малоизвестных американских журналах. Лишь позднее теории Гиббса воздали должное.
Истоки атомно-молекулярной теории восходят к первым попыткам Бойля (1627-1691гг.) и Ньютона (1648-1727гг.) представить теплоту как молекулярное движение. Тогда еще не существовало количественной кинетической теории. В 1738 году Бернулли предложил первые наброски кинетической теории газов. М.В.Ломоносов в 1745-1747гг. более или менее последовательно развивал молекулярно-кинетическую теорию тепла. В частности, он предположил существование абсолютного нуля температур, обосновал превращение механического движения в тепловое. Однако, в то время атомистическая теория Ломоносова была отвергнута большинством приверженцев другого термодинамического подхода. Термодинамический метод - описательный метод. Он базируется на результатах эксперимента. Основные достижения термодинамики связаны с работами Карно (работа термодинамической системы за цикл), с построением классической термодинамики в 1850г. Клаузиусом и Томпсоном (лорд Кельвин). Развитие физики в значительной мере в 18 - 19 веках было сопряжено борьбой сторонников термодинамического и молекулярно-кинетического представлений. Особенно обострилась эта борьба на рубеже XIX и XX столетий между сторонниками термодинамического подхода (Оствальд, Мах) и молекулярно-кинетического направления (Клаузиус, Максвелл, Больцман). Для Больцмана эта борьба закончилась трагически. Его особенно донимали вопросы типа «А видел ли кто эти молекулы?» Он покончил жизнь самоубийством в 1906г. Больцман не знал, что еще в 1828 году английский ботаник Роберт Броун наблюдал, как под действием молекул движутся микроскопические частички. Сейчас броуновское движение пылинок в луче света наблюдает каждый из нас, и это служит лучшим подтверждением их существования. Истинность учения Больцмана была доказана поляком Смолуховским в работе по броуновскому движению. Современная физика включает в себя как составные части термодинамику и статистическую физику.
Законы термодинамики
Первый закон термодинамики отражает закон сохранения энергии
dQ=dU + dA. Количество тепла dQ, переданное телу, идет на увеличение его внутренней энергии dU и совершение работы dA.
Второй закон термодинамики
Самопроизвольно идет процесс перехода системы из состояния с меньшей термодинамической вероятностью в состояние с большей термодинамической вероятностью.
- S0 Энтропия замкнутой системы не убывает. Поскольку энтропия характеризует степень хаотизации системы, то второе начало термодинамики говорит о том, что хаос в замкнутых системах должен только возрастать. Такой вывод привел Больцмана к представлению о тепловой смерти Вселенной.
- Невозможно прямое преобразование тепловой энергии в механическую без потерь.
Третий закон термодинамики свидетельствует о невозможности достижения абсолютного нуля температур.
