
Лабораторная работа3
.docxКим С.Д.
ММЭ(б)-21
Стр.
Лабораторная работа № 3
Марковский процесс с дискретными состояниями и дискретным временем
Задание:
Задана
матрица перехода системы
 ,
,
где
c=0,002⋅k,
k –
номер фамилии студента в списке
преподавателя. Дано начальное распределение
вероятностей состояний системы S:
На
печать выдать
 ,
,
 .
Вычислить и выдать на печать
.
Вычислить и выдать на печать
 ,
,
 ,
,
 ,
,
 ,
,
 .
Решить систему
.
Решить систему

и
выдать на печать
 и
и
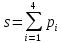 .
Взять
.
Взять
 =(1;0;0;0)
и выполнить те же вычисления.
=(1;0;0;0)
и выполнить те же вычисления.
Решение:
Задаем матрицу и начальные значения:
>
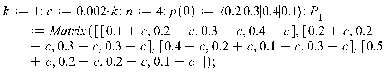
![]()
![]()
![]()
![]()

Пусть z – количество переходов системы S из состояния Si в состояние Sj. Рассчитаем матрицу вероятностей переходов:
>
![]()
![]()

Проверка матрицы вероятностей переходов через z шагов:
>

![]()
![]()
![]()
![]()
Вычисление
матрицы переходов после 1, 2, 4 и 8 шагов
из заданного начального распределения



Аналогично
для



Решение системы уравнений для финальных вероятностей переходов p1, p2, p3 и p4:
>

>

![]()
Проверка финальных вероятностей:
>
![]()
![]()
