Расчет сифона

Сифоном называется весьма короткий трубопровод, если некоторая его часть располагается выше уровня жидкости, находящейся в открытом резервуаре, откуда происходит подача жидкости.

Определить расход и Z_max, если известны длина, диаметр, эквивалентная шероховатость, разность уровней в баках.

Из уравнения Бернулли для сечений 1-1 и 2-2.

Даже такая простенькая задача напрямую не решается.

Почти все реальные, инженерные гидравлические задачи решаются методом последовательных приближений. Вариантов может быть много. Например:

1. Считаем, что режим движения жидкости турбулентный и имеет место квадратичная зона сопротивления. .

2. Выбираем формулу для расчета l, определяем ее, сумму местных сопротивлений, скорость.

3. Находим число Рейнольдса и делаем проверку на правильность первого допущения.

4. Если допущение справедливо, то расчет закончен. Если нет, то возвращаемся к пункту 2. Количество итераций зависит от требуемой точности расчетов.

Найдем максимальную высоту подъема трубы Z max

Из уравнения Бернулли для сечений 1-1 и 3-3.

.

. Когда Z будет максимальной?

,

Обычно допускается Z_max=7 - 8 м

Расчет простого короткого трубопровода при подаче жидкости из напорного бака

Подача воды на технологические нужды производится из открытого напорного бака А по короткому трубопроводу B постоянного сечения длиной l в расходную емкость С. Должна быть обеспечена подача Q.

Подобрать необходимый диаметр труб.

Из уравнения Бернулли для сечений 1-1 и 2-2.

, ,

Находим диаметр.

Задача напрямую не решается

, .

Используем метод итераций.

1. Предположим, что потери по длине =0. (l=0) Находим d в первом приближении.

2. Находим скорость, число Рейнольдса, l и вычислим d во втором приближении.

3. Делаем несколько итераций, количество которых зависит от требуемой точности расчетов.

Графическое решение задачи

1. Предположим, что потери по длине =0. (l=0) Находим минимальный d

2. Задаемся шагом изменения диаметра, задаемся несколькими диаметрами и для каждого из них рассчитываем расход.

3. Строим график зависимости расхода от диаметра.

Решением будет пересечение линии требуемого расхода с графиком.

Что еще необходимо учесть при окончательном выборе диаметра до оформления заказа на трубы?

Последовательное соединение простых трубопроводов

Несколько труб различной длины, разного диаметра и содержащих разные местные сопротивления соединены последовательно.

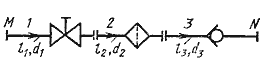
В данном случае имеем 3 участка с разными диаметрами труб.

Особенностью является равенство расходов в каждой из труб Q₁= Q₂= Q₃=Q.

Общая потеря составит сумму потерь на участках

.

Из уравнения Бернулли для сечений M и N

,

Параллельное соединение простых трубопроводов

Для простоты допустим, что трубопроводы расположены в горизонтальной плоскости.

Обозначим полные напоры в точках М и N соответственно через Н_M и Н_N

Расход в основной магистрали — Q, а в параллельных трубопроводах - Q₁, Q₂, Q₃ . Q = Q₁ + Q₂+Q₃.

Суммарные потери напора в этих трубопроводах

Из уравнения Бернулли для сечений в точках М и N: следует, что потери напора в параллельных трубопроводах равны между собой. .

Их можно выразить в общем виде через соответствующие расходы следующим образом

Изложенные соотношения и правила для параллельных трубопроводов справедливы и в том случае, когда трубопроводы 1, 2, 3 и т. не сходятся в одной точке N₁,а подают жидкость в разные места, но с одинаковыми давлениями и равными нивелирными высотами. (Истечение в атмосферу на одном уровне)

Если же последнее условие не соблюдается, то рассматриваемые трубопроводы нельзя считать параллельным, а следует относить к разряду разветвленных трубопроводов .

Графическое решение