
Кафедра прикладной математики
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ»
кафедра прикладной математики и информатики
Горчакова Нина Федоровна
Методические указания к выполнению индивидуальных типовых расчетов по математической статистике (электронная версия)
Саратов 2012
На конкретном примере (выборочные данные) дана методика выполнения типовых расчетов по темам:
Построения интервального статистического ряда распределения (типовой расчет №1).
Вычисление выборочных характеристик ряда распределения (типовой расчет №2).
Графическое изображение рядов распределения (типовой расчет №3).
Расчет теоретической нормальной кривой распределения (типовой расчет №4).
Проверка гипотеза о нормальном законе распределения по критерию согласия Пирсона χ2 (типовой расчет №5).
Задание.
По выборочным данным, представленным в таблице №11-38, требуется выполнить типовые расчеты:
Типовой расчет №1:
Построить интервальный статистический ряд распределения.
Типовой расчет №2:
Вычислить выборочные характеристики статистического ряда: начальные моменты
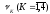 ,
среднюю арифметическую
,
среднюю арифметическую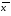 ,
центральные моменты
,
центральные моменты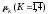 ,
дисперсию
,
дисперсию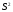 ,
среднее квадратическое отклонениеS
, коэффициенты ассиметрии
,
среднее квадратическое отклонениеS
, коэффициенты ассиметрии
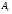 и
эксцесса
и
эксцесса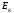 ,
медиану
,
медиану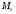 ,
моду
,
моду ,
коэффициент вариации
,
коэффициент вариации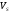 .
.Дать экономическую интерпретацию выборочным числовым характеристикам.
Типовой расчет №3:
Построить гистограмму, полигон, кумуляту, огиву.
Сделать вывод о форме ряда распределения по виду гистограммы и полигона, а также по значениям коэффицицентов
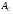 и
и
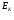 .
.
Типовой расчет №4:
Рассчитать теоретическую нормальную кривую распределения
 и построить ее на эмпирическом графике.
и построить ее на эмпирическом графике.Сделать вывод о согласовании между теоретическим и эмпирическим распределениями.
Типовой расчет №5:
Проверить
гипотезу о нормальном законе распределения
по критерию согласия Пирсона ( )
на заданном уровне значимости α = 0,05.
)
на заданном уровне значимости α = 0,05.
Типовой расчет №1
Построение интервального статистического (вариационного) ряда распределения.
Дана выборка обследования 100 однотипных предприятий получены данные объема основных фондов (табл.1.1).
Таблица I.I
Объем основных фондов 100 (млн. руб.) предприятий легкой промышленности
|
5,56 |
5,43 |
5,47 |
5,47 |
5,33 |
5,37 |
5,43 |
5,54 |
5,61 |
|
5,33 |
5,43 |
5,61 |
5,11 |
5,43 |
5,33 |
5,54 |
5,33 |
5,11 |
|
5.54 |
5,43 |
5,33 |
5,54 |
5,43 |
5,43 |
5,43 |
5,33 |
5,11 |
|
5,43 |
5,43 |
5,33 |
5,43 |
5,40 |
5,43 |
5,47 |
5,68 |
5,47 |
|
5,43 |
5,68 |
5,21 |
5,33 |
5,58 |
5,47 |
5,47 |
5,21 |
5,54 |
|
5,64 |
5,47 |
5,27 |
5.27 |
5,37 |
5,33 |
5,47 |
5,47 |
5,54 |
|
5,40 |
5,58 |
5,47 |
5,27 |
5,05 |
5,79 |
5,79 |
5,64 |
5,64 |
|
5,71 |
5,85 |
5,47 |
5,47 |
5,43 |
5,47 |
5,54 |
5,64 |
5,64 |
|
5,79 |
5,93 |
5,33 |
5,68 |
5,43 |
5,61 |
5,54 |
5,64 |
5,54 |
|
5,39 |
5,33 |
5,21 |
5,68 |
5,54 |
5,33 |
5,21 |
5,21 |
5,81 |
|
5,27 |
5,64 |
5,27 |
5,27 |
5,33 |
5,37 |
5,27 |
5,54 |
5,54 |
|
5,47 |
|
|
|
|
|
|
|
|
Этапы построения интервального статистического (вариационного) ряда распределения.
1. Определение
среди имеющихся наблюдений (табл.1.1)
минимального
Хmin.
и
максимального
Хmах
значения
признака. В
данном примере
это будут
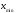 =5,05
и
=5,05
и =5,93.
=5,93.
Определение размаха варьирования признака
R
=
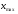 -
- =
5,93 - 5,05 = 0,88
=
5,93 - 5,05 = 0,88
Определение длины интервала по формуле
h
=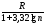 ,
гдеn
- объем выборки.
,
гдеn
- объем выборки.
В данном примере h = 0.88/1+3.32*lg100=0.11
Определение граничных значений интервалов (
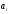 ;
; ).
).
Так,
как
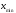 и
и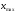 являются случайными величинами,
рекомендуется отступить влево от
нижнего предела варьирования(
являются случайными величинами,
рекомендуется отступить влево от
нижнего предела варьирования( ).
).
За
нижнюю границу первого интервала
предлагается принимать величину, равную
 =
=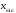 –h/2.
–h/2.
Если
оказывается, что
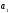 <
0 , хотя
по смыслу величина не отрицательная,
то можно принять
<
0 , хотя
по смыслу величина не отрицательная,
то можно принять
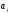 =
0.
=
0.
Верхняя
граница первого интервала
 =
=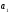 +h.
Тогда, если
+h.
Тогда, если
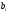 – верхняя границаi-го
интервала (причем
– верхняя границаi-го
интервала (причем
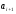 =
= ),
то
),
то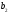 =
= +h,
+h,
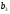 =
=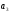 +h
и т.д. Построение интервалов продолжается
до тех пор, пока начало следующего по
порядку интервала не будет равным
или больше
+h
и т.д. Построение интервалов продолжается
до тех пор, пока начало следующего по
порядку интервала не будет равным
или больше
 .
.
В примере граничные значения составят:
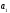 =5.05-0.11/2=4,995;
=5.05-0.11/2=4,995;
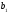 =4.995+0.11=5.105;
=4.995+0.11=5.105; =5.105;
=5.105;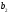 =5.105+0.11=5.215
и т.д.
=5.105+0.11=5.215
и т.д.
Границы последовательных интервалов записывают в графе I
таблицы 1.2.
Группировка результатов наблюдения.
Просматриваем
статистические данные в том порядке, в
каком они записаны в таблице I.I,
и значения признака разносим по
соответствующим интервалам, обозначая
их так: (по одному штриху для каждого
наблюдения). Так как граничные значения
признака могут совпадать с границами
интервалов, то условимся в каждый
интервал включать варианты, большие,
чем нижняя граница интервала ( >
>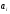 ),
и меньшие или равные верхней границе
(
),
и меньшие или равные верхней границе
(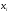 <
<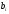 ).
Общее количество штрихов, отмеченных
в интервале (табл.1.2, графа 2) даст его
частоту (табл. 1.2, графа 3). В результате
получим интервальный статистический
ряд распределения частот (табл.1.2 графа
I
и 3).
).
Общее количество штрихов, отмеченных
в интервале (табл.1.2, графа 2) даст его
частоту (табл. 1.2, графа 3). В результате
получим интервальный статистический
ряд распределения частот (табл.1.2 графа
I
и 3).
Примечание. Число интервалов обычно берут равным от 7 до 11 в зависимости от числа наблюдений и точности измерений с таким расчётом, чтобы интервалы были достаточно наполнены частотами. Если получают интервалы с нулевыми частотами, то нужно увеличить ширину интервала (особенно в середине интервального ряда).
Таблица 1.2
Интервальный ряд распределения объемов основных фондов 100 предприятий
|
Интервалы( |
Подсчет частот
|
Час-тота
|
Накопленная частота mHi |
|
1 |
2 |
3 |
4 |
|
4,99 - 5,10 5,10 - 5,21 3,21 - 5,32 5,32 - 5,43 5,43 - 5,54 5,54 - 5,65 5,65 - 5,76 5,76 - 5,87 5,87 - 5,98 |
● ●●●●●●●● ●●●●●●● ●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●● ●●●●●●●●●●●●●●●●●●●●●●●●●● ●●●●●●●●●●●●● ●●●●● ●●●●● ● |
1 8 7 34 26 13 5 5 1 |
1 9 16 50 76 89 94 99 100 |
|
∑ |
|
100 |
|
Соответствие между 1 и 3 столбцами является интервальным вариационным рядом абсолютных частот.
Вопросы для самопроверки
В чем отличие генеральной совокупности от выборочной совокупности?
Что называется статистическим (вариационным) рядом распределения?
Виды рядов распределения?
Простой ряд и по сгруппированным данным?
Как перейти от интервального вариационного ряда к дискретному ряду?
В чем отличие абсолютной частоты от относительной частоты?
Какие задачи решает теория вероятностей и математическая статистика?

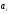 ;
; )
)