Ещё пример задания:

P-26. Сколько различных решений имеет система логических уравнений

(x₁  x₂)  (x₁  x₂  x₃)  (x₁  y₁) = 1

(x₂  x₃)  (x₂  x₃  x₄)  (x₂  y₂) = 1

(x₃  x₄)  (x₃  x₄  x₅)  (x₃  y₃) = 1

(x₄  x₅)  (x₄  x₅  x₆)  (x₄  y₄) = 1

(x₅  x₆)  (x₅  y₅) = 1

x₆  y₆ = 1

где x₁, …, x₆, y₁, …, y₆, – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Решение (вариант 1, битовые цепочки, М.А. Ройтберг):

1. перепишем систему с более понятными обозначениями:

2. решением уравнения будут два набора логических переменных, и, которые можно представить в виде битовых цепочек:

,

3. первые 4 уравнения однотипны, отличаются только сдвигом номеров переменных; рассмотрим сначала их

4. сомножитель должен быть равен 1, поэтому в цепочкене должно быть двух идущих подряд нулей (иначеи все произведение равно 0)

5. сомножитель должен быть равен 1, поэтому если в цепочке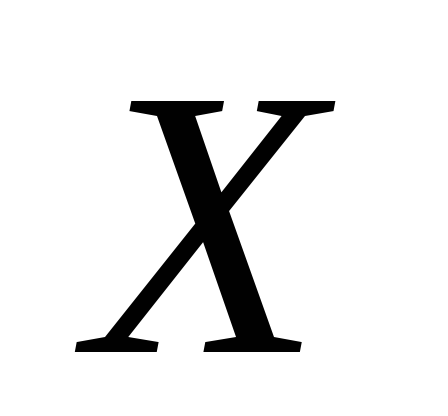появились две единицы подряд, то дальше идут только единицы (иначеи все произведение равно 0)

6. таким образом, если не учитывать (пока) сомножитель в каждом из уравнений, существует всего 7 допустимых цепочек, каждая из которых определяется положением последнего нуля (0 – вообще нет нуля):

7. теперь рассмотрим сомножители , которые тоже должны быть равны 1; если, то сразу получаем; если же, то есть два варианта

8. таким образом, для каждой цепочки количество соответствующих цепочекравно, где черезобозначено число единиц в цепочке

9. в цепочке есть 6 единиц, в цепочкахи– по пять, в цепочкахи– по четыре, ви– по три

10. поэтому общее число решений вычисляется как 2⁶ +2∙(25⁵⁵⁵⁵+ 2⁴+ 2³) = 64 + 2∙(325⁵⁵⁵ + 16 + 8) = 176

11. Ответ: 176.

Решение (вариант 2, последовательное подключение уравнений, метод отображений):

1. перепишем систему с более понятными обозначениями:

2. первые 4 уравнения однотипны, отличаются только сдвигом номеров переменных

3. первое и второе уравнения связаны только ч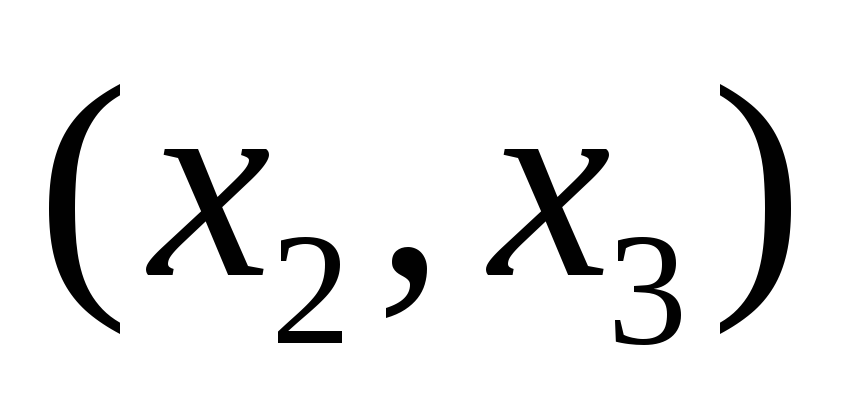ерез пару , второе и третье – только через пару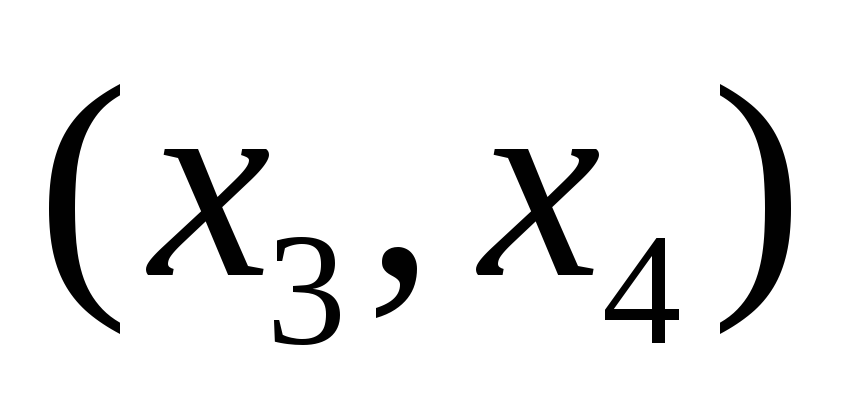и т.д.;

4. таким образом, для того, чтобы определить количество решений системы из первых двух уравнений, нам нужно построить отображениевсех парна пары; это значит, для каждого варианта парыопределить количество различных решений, соответствующих всем возможным парам

5. покажем это на примере; рассмотрим второе уравнение:

6. пусть , тогда первая скобка равна 0 и решений нет, никаких стрелок в таблице отображения пока нет:

7. если , получаем уравнение

Которое имеет два решения: или 1, а; при этом параотображается на одну паруи на одну пару:

8. если , получаем уравнение

Здесь и , имогут принимать любые значения (0 или 1), всего получается 4 решения. Поскольку, два решения соответствуют паре, а другие два – паре:

9. наконец, если , получаем уравнение

Здесь обязательно , аможет быть любым (0 или 1), всего 2 решения, и оба они соответствуют паре:

10. теперь обозначим через ичисло решений, соответствующих связующим парам (0,0), (0,1), (1,0) и (1,1), соответственно

11. как видно из схемы, при подключении нового уравнения эти значения преобразуются по рекуррентным формулам:

12. используя эти формулы, заполняем таблицу, начиная со всех значений, равных 1:

    Число уравнений	0	1	2	3	4
    a	1	2	2	4	4
    b	1	2	2	4	4
    c	1	1	2	2	4
    d	1	3	8	18	40

13. итак, мы получили, что система из первых четырёх уравнений имеет всего 4+4+4+40=52 решения; теперь подключаем пятое равнение, которое связано с первыми четырьмя через пару :

14. заметим, что последнее, 6-е уравнение, связано с предыдущими только через , поэтому, подключая 5-е уравнение, строим отображение пары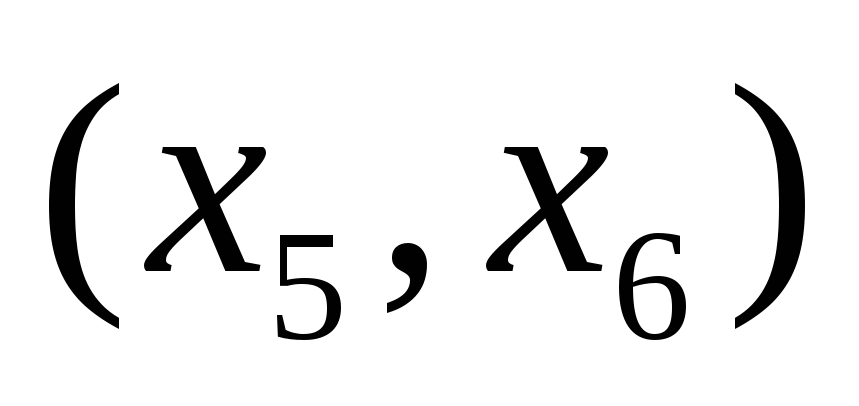на:

при решений нет

при одно решение (), отображается на

при два решения (), оба при

при два решения (), оба при

15. из таблицы (см. выше) следует, что система из 4-х уравнений имеет 4 решения при , которые не дают решений системы из 5 уравнений;

4 решения при , которые дают по 1 решению (всего4при);

4 решения при , которые дают по 2 решения (всего8при);

40 решений при , которые дают по 2 решения (всего80при);

16. всего получаем 8решений прии84решения при;

17. теперь подключаем 6-е уравнение

18. при 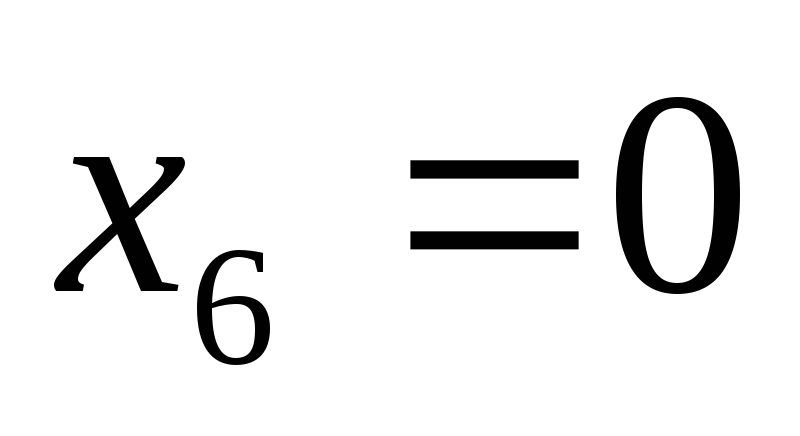это уравнение имеет одно решение (), поэтому вся система уравнений имеет 8 решений с

19. при последнее уравнение имеет два решение (), поэтому вся система уравнений имеет 2·84 = 168 решений с

20. Ответ: 8 + 168 = 176.