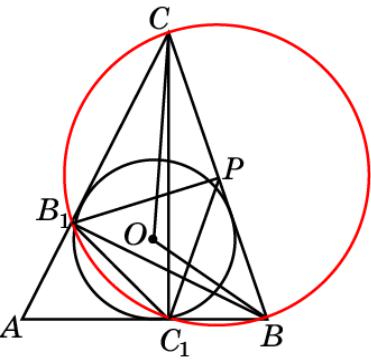
Упражнение 32
В остроугольном треугольнике ABC проведены высоты BB1 и CC1, BC = 24, B1C1 = 12, O – центр
вписанной окружности. Найдите угол BOC.
Решение. Рассмотрим окружность с диаметром BC, P – ее центр. Она пройдет через точки B1 и C1.
Треугольник PB1C1
равносторонний, следовательно, угол B1PC1 равен 60о. Углы B1BC1
и B1BC1 опираются на дугу B1C1,
следовательно, равны 30о.
Угол A треугольника ABC равен 60о. Следовательно, угол BOC равен 120о.
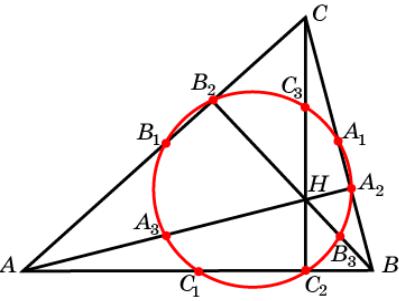
Окружность Эйлера
Пусть в треугольнике ABC точки A1, B1, C1 обозначают середины
сторон противоположных соответствующим вершинам; H – точка пересечения высот треугольника; A2, B2, C2 – основания высот,
опущенных из соответствующих вершин; A3, B3, C3 – середины отрезков AH, BH и CH. Докажите, что точки A1, B1, C1, A2, B2, C2, A3, B3, C3 принадлежат одной окружности, называемой окружностью девяти Эйлера.
Решение дано на следующем слайде.
|
|
|
|
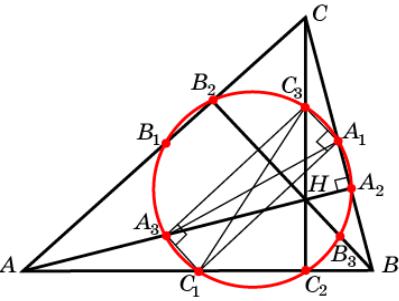
Решение |
Проведем окружность через точки C1, C2, C3. Отрезок C1C3 будет ее |
||||
диаметром. Так как A1C1 – средняя линия треугольника ABC, то A1C1 |
||||
|| AC. Так как A1C3 |
– средняя линия треугольника BCH, то A1C3 || BH. |
|||
Значит, |
C AC |
90 |
||
1 |
1 3 |
и, следовательно, точка A1 принадлежит этой |
||
окружности. |
|
Аналогично, Так как A3C3 – средняя линия |
||
треугольника AHC, то A3C3 || AC. Так как C1A3 – средняя линия |
||||
треугольника ABH, то C A || BH. Значит, C1 A3C3 90 и, |
||||
|
|
|
1 |
3 |
следовательно, точка A3 |
принадлежит этой окружности. |
|
A1C1A3C3 – прямоугольник и, значит, |
|
A1A3 – диаметр окружности. Так как |
|
A1 A2 A3 90 , то A2 принадлежит |
|
окружности. Таким образом, мы |
|
доказали, что этой окружности |
|
принадлежат точки A1, A2, A3. |
|
Аналогично доказывается, что этой |
|
окружности принадлежат точки B1, |
|
B , B . |
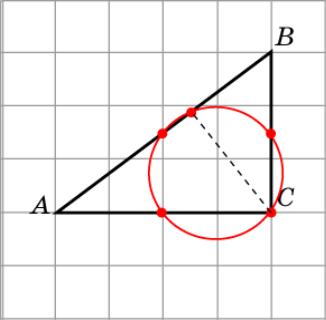
Окружность Эйлера 2
Изобразите окружность Эйлера для треугольника ABC. Найдите ее радиус.
Ответ. 2,5.
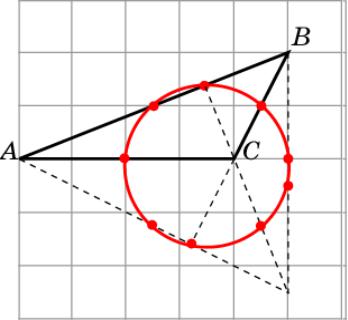
Окружность Эйлера 3
Изобразите окружность Эйлера для треугольника ABC.
Ответ.
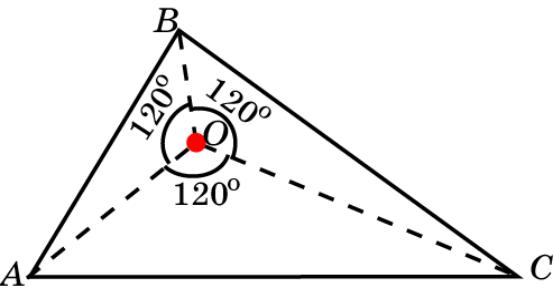
Точка Торричелли
Точкой Торричелли треугольника ABC называется такая точка O, из которой стороны данного треугольника видны под углом 120о, т.е. углы AOB, AOC и BOC равны 120о. Докажите, что в случае, если все углы треугольника меньше 120о, точка Торричелли существует.
Решение дано на следующем слайде.
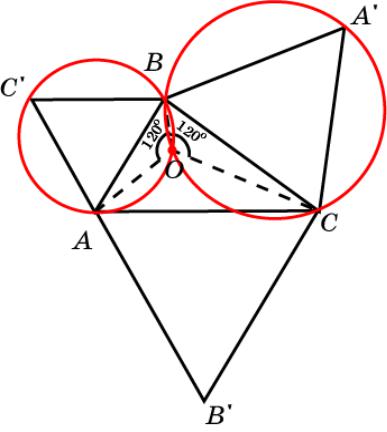
Решение
На стороне AB треугольника ABC построим равносторонний треугольник ABC', и опишем около него окружность. Отрезок AB стягивает дугу этой окружности величиной 120о. Следовательно, из точек этой дуги, отличных от A и B, отрезок AB виден под углом 120о.
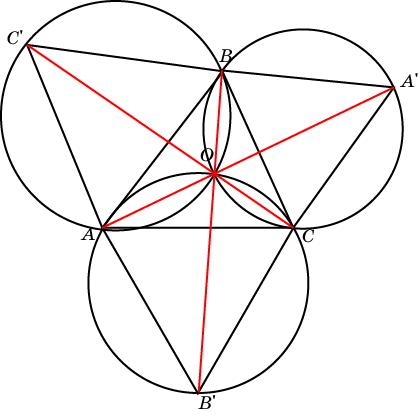
Упражнение 35
На сторонах треугольника ABC, углы которого меньше 120о, во внешнюю сторону от него построили равносторонние треугольники. Докажите, что отрезки, соединяющие вершины исходного треугольника и противоположные им вершины равносторонних треугольников, пересекаются в одной точке.
Решение. Докажем, что искомой точкой пересечения является точка Торричелли O.
Угол AOB равен 120о. Угол BOA’ равен 60о. Следовательно, точка O принадлежит отрезку AA’. Аналогично доказывается, что точка O принадлежит отрезкам BB’ и CC’.
Упражнение 36
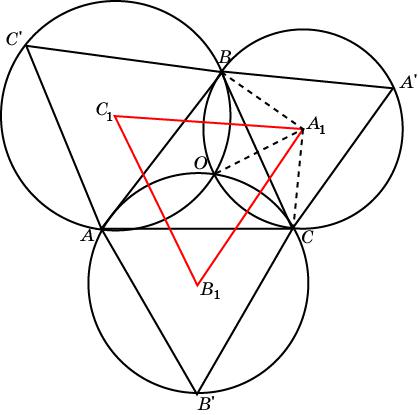
На сторонах треугольника ABC во внешнюю сторону от него построили равносторонние треугольники. Докажите, что центры окружностей, описанных около этих треугольников, являются вершинами равностороннего треугольника.
Решение. Угол BA1C равен 120о. Прямые A1B1 и A1C1 содержат биссектрисы углов OA1C и OA1B
соответственно. Следовательно, угол A1 треугольника A1B1C1 равен
60о. Аналогично доказывается, что углы B1 и C1 этого треугольника
равны 60о. Значит, треугольник A1B1C1 равносторонний.