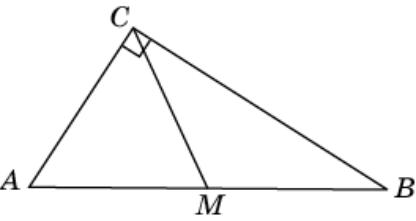
Упражнение 22
Докажите, что если медиана треугольника равна половине стороны, к которой она проведена, то этот треугольник прямоугольный.
Доказательство. В этом случае основание M медианы равноудалено от вершин треугольника и, следовательно, является центром описанной окружности. Угол C опирается на диаметр AB, следовательно, равен 90о.
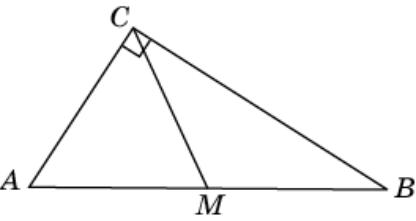
Упражнение 23
Гипотенуза прямоугольного треугольника равна 4. Найдите радиус описанной окружности.
Ответ: 2.
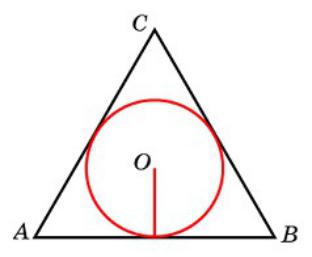
Упражнение 24
Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
Ответ: 2.
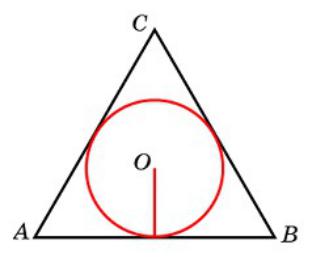
Упражнение 25
Радиус окружности, вписанной в правильный треугольник, равен 3. Найдите высоту этого треугольника.
Ответ: 9.
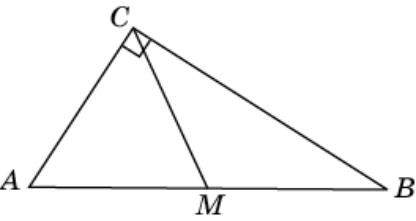
Упражнение 26
Медиана, проведенная к гипотенузе прямоугольного треугольника, равна 3 и делит прямой угол в отношении 1:2. Найдите меньший катет треугольника.
Ответ: 3.
Упражнение 27
Проекции двух сторон остроугольного треугольника АВС на прямую АС имеют длины 6 см и 4 см. Какую длину имеют проекции медиан этого треугольника на ту же прямую?
Ответ: 1 см, 7 см и 8 см.
Упражнение 28
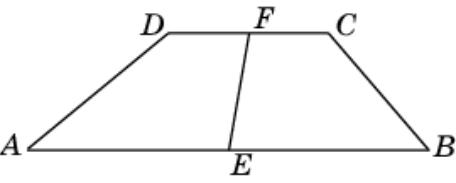
Основания трапеции равны 20 и 8, углы при большем основании равны 40о и 50о. Найдите отрезок, соединяющий середины оснований.
Ответ: 6.
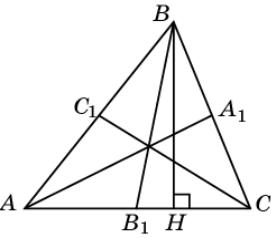
Упражнение 29
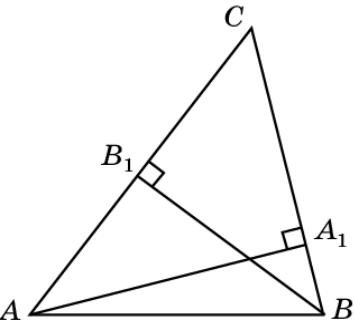
Докажите, что если AA1, BB1 – высоты треугольника ABC, то угол A1AC равен углу B1BC.
Доказательство. Прямоугольные треугольники A1AC и B1BC имеют общий острый угол C. Следовательно, равны и два других их острых угла A1AC и B1BC.
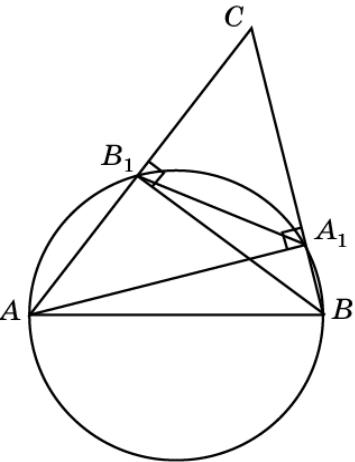
Упражнение 30
Докажите, что если AA1, BB1 – высоты треугольника ABC, то угол B1A1C равен углу BAC.
Доказательство. Рассмотрим окружность с диаметром AB. Угол B1A1C равен 90о минус угол
B1A1A. Углы B1A1A и B1BA равны, как вписанные углы,
опирающиеся на одну дугу. Угол BAC равен 90о минус угол B1BA.
Следовательно, равны углы B1A1C
и BAC.
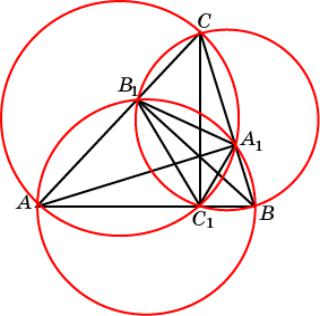
Упражнение 31
Докажите, что если AA1, BB1, CC1 – высоты треугольника ABC, то угол A1C1C равен углу
B C C.
Доказательство. На сторонах треугольника ABC, как на диаметрах, опишем окружности. Они пройдут
через точки A1, B1, C1. Угол A1C1C равен углу A1AC как углы,
опирающиеся на одну дугу A1C.
Угол A1AC равен углу B1BC. Угол B1BC равен углу B1C1C, как углы, опирающиеся на одну дугу B1C. Следовательно, угол A1C1C равен углу B1C1C.