§ 6.6. Проверка гипотезы о равенстве параметров двух нормально распределенных генеральных совокупностей

Пусть заданы две нормально распределенные генеральные совокупности. Рассмотрим случаи проверки гипотез о равенстве параметров этих совокупностей. Возможны следующие случаи:

1. Гипотеза о равенстве их средних

Статистика критерия для проверки гипотезы о равенстве средних нормально распределенных генеральных совокупностей при известных дисперсиях имеет вид

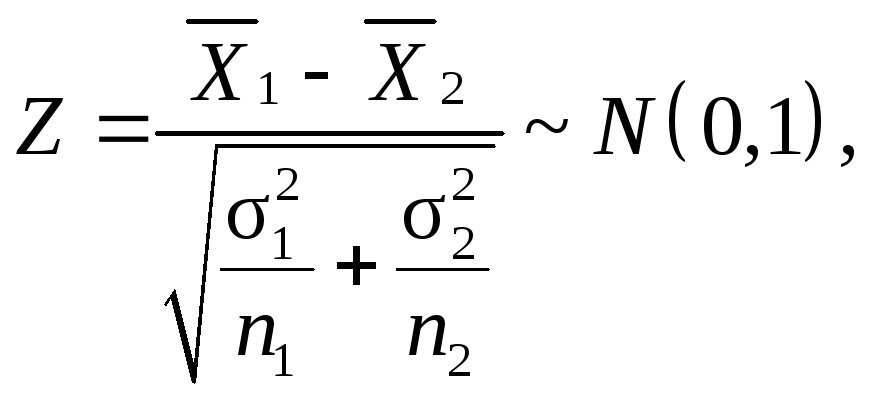
где n₁, n₂ — объемы выборок;

—выборочные средние исследуемых генеральных совокупностей;

—известные дисперсии генеральных совокупностей.

Критическая область критерия при уровне значимости  определяется неравенствами

z^*  − при альтернативной гипотезе

z^*  − при альтернативной гипотезе ,

z^* < − при альтернативной гипотезе

При этом гипотеза Н₀ не отвергается (принимается) на уровне значимости , если соответствующий двусторонний или односторонний доверительный интервал накрывает наблюдаемое значение критерия z^*; в противном случае гипотеза Н₀ отклоняется.

Статистика критерия для проверки гипотезы о равенстве средних нормально распределенных генеральных совокупностей при неизвестных, но равных дисперсиях имеет вид

n₁, n₂ — объемы выборок;

—выборочные средние исследуемых генеральных совокупностей;

—исправленные выборочные дисперсии исследуемых генеральных совокупностей.

Статистика имеет распределение Стьюдента с степенями свободы.

Критическая область критерия при уровне значимости  определяется неравенствами

t^*  − при альтернативной гипотезе

t^*  − при альтернативной гипотезе ,

t^* < − при альтернативной гипотезе

При этом гипотеза Н₀ не отвергается (принимается) на уровне значимости , если соответствующий двусторонний или односторонний доверительный интервал накрывает наблюдаемое значение критерия t^*; в противном случае гипотеза Н₀ отклоняется.

Статистика критерия для проверки гипотезы о равенстве средних двух нормально распределенных генеральных совокупностей при неизвестных, но неравных дисперсиях имеет вид

n₁, n₂ — объемы выборок;

—выборочные средние исследуемых генеральных совокупностей;

—исправленные выборочные дисперсии исследуемых генеральных совокупностей.

Дальнейшие действия по проверки гипотезы аналогичны предыдущему случаю.

2. Гипотеза о равенстве их дисперсий .

Статистика критерия для проверки гипотезы о равенстве дисперсий двух нормально распределенных генеральных совокупностей при неизвестных средних имеет вид

Статистика имеет распределение Фишера с степенями свободы.

Критическая область критерия при уровне значимости  определяется неравенствами

−при альтернативной гипотезе

−при альтернативной гипотезе

При этом гипотеза Н₀ не отвергается (принимается) на уровне значимости , если соответствующий двусторонний или односторонний доверительный интервал накрывает наблюдаемое значение критерия t^*; в противном случае гипотеза Н₀ отклоняется.

Пример.

При обработке выборок объемов =30 и=20 из генеральных совокупностей с известными дисперсиями иполучены для математических ожиданий и. На уровне значимости 5% проверить гипотезу о равенстве математических ожиданий против конкурирующей гипотезы о том, что.

Имеем: ;.

Значение α= 0,05; 1-α=0,95. По таблице 2 найдем z_0,95квантиль порядка 0,95 стандартного нормального распределения:z_0,95=1,645. Вычислим наблюдаемое значение критерия<- z_0,95=-1,645. Следовательно, принимается гипотеза .