Дискретна математика

3)якщо правило k має праворуч di, то правило k + 1 ліворуч також повинне мати di;

4)не повинно бути ділянок поруч, які повторюються.

Убудь-якому випадку є послідовності правил виведення. Виберемо з них максимальну. Нехай її довжина m.

Тоді задамо мову як підмножину E у такий спосіб:

d0 d0 e1

по одному символу;

d0 en

d0 en en

Нехай буде М слів цієї довжини. Тоді:

d0 1d1

d0 m dm

d1 e1, d1 e1d1

d1 en , d1 end1

Тоді можна уникнути появи слів цього виду:

-видаленням цих правил;

-перебором усіх закінчених комбінацій довжини m і їх видаленням, а потім перебором усіх незакінчених комбінацій при довжині рівній m забезпеченням неможливості продовження слів так, як того

вимагає послідовність m

Ще один варіант доведення, запропонований студентом Гоголєвим (гр. ФІ-01).

Нехай задана автоматна граматика G = <E, D, P, d0>. Покажемо, що L(G) - регулярна множина. Наведемо доказ індукцією по кількості нетерміналів.

1. База індукції. |D|=1.

У цьому випадку можна записати: P = {d0→α1d0, d0→α2d0, …, d0→αnd0, d0→β1, d0→β2, … d0 →βm} = K A (див. рис.), αi,, βj належать E*.

Наведемо відповідний рисунок:

Кожному слову в L(G) взаємно однозначно відповідає деякий ланцюг у цьому графі з початком у

вершині d0 і кінцем у деякій вершині з множини K. Зрозуміло, що "ланцюг бігає" по петлях з множини A

91

доки не закінчитися у вершині з множини K (кінець). Тепер практично очевидно, що можна записати відповідний регулярний вираз: {α1, α2 , … αn }* ∙ { β1 , β2 , … βm }...

Множини {α1, α2, …, αn} і {β1, β2, …, βm} регулярні, тому що кожне слово αi і βj може бути отримано скінченим числом конкатенацій літер алфавіту. Потім ці множини можна одержати скінченим числом операцій об'єднання регулярних множин. База індукції доведена.

2.Індукційне припущення: нехай твердження виконується для |D| ≤ k.

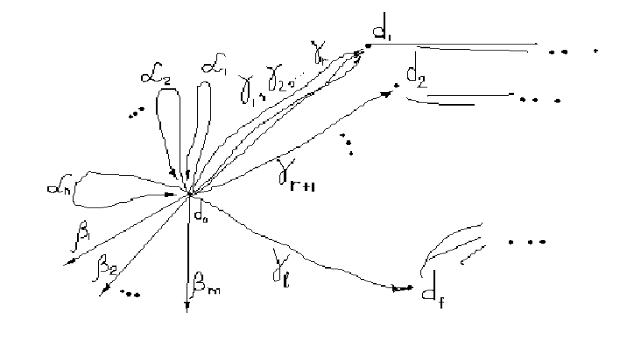
3.Доведемо, що твердження виконується для |D| = k+1. Випишемо всі правила вигляду d0→β, K= {d0→β1, d0→β2, …,d0 → βm} Також випишемо всі правила вигляду d0→αd0, A = {d0→α1d0, d0→α2d0, …, d0→αnd0 }... І правила, що залишилися (у яких міститься нетермінал d0 з лівої сторони) вигляду d0>γdi (i≠0), B = {d0→γ1d1,

d0→γ2d1, d0→γ3d1 ,…, d0→γrd1d0→γr+1d2,…d0→γldf}...

Наведемо відповідний граф.

Очевидно, що кожному слову мови L(G) взаємно однозначно відповідає деякий ланцюг у цьому графі. Цей ланцюг може дуже багато разів проходити через вершину d0 і закінчуватися або в βi (i=1,..,m), або десь у правій частині графа (див. рис.). Розглянемо "шматки" кожного такого ланцюга, які отримують "вириванням" усіх вершин d0, що входять у наш ланцюг (вони можуть бути як завгодно великими). Усі ці "шматки" (які взагалі, у принципі можуть виникнути) розіб'ємо на f множин. Перша множина I1 − ті "шматки", які отримують після застосування якогось із правил d0→γid1 (i=1,.. r), друга множина I2 − ті "шматки", які отримують після застосування якогось із правил d0→γjd2 і т.д. до множини If "шматків", які отримують після застосування правил вигляду d0→γjdf (не треба забувати, що є ще "шматки" α1, α2, …, αn)...

За допомогою припущення індукції доведемо, що кожне з цих f множин є регулярною. Після цього ці множини Ik (k =1,.. f) чимось не будуть відрізнятися від αi і буде просто провести міркування аналогічні міркуванням бази індукції ("склеємо" їх у всіх можливих послідовностях за допомогою операції ітерації). Однак не варто забувати про "останні шматки" ланцюжків, що зіграють роль аналогічну ролі βi в доведенні бази. З цими шматками треба окремо попрацювати і приєднати їх наприкінці слова за допомогою операції конкатенації. Це був ліричний відступ, а тепер перейдемо до строгих викладок.

Для кожного di (із правил B) розглянемо граматику Gi = <E, D\{d0}, Pi, di >. В Pi не входять правила з K

A B і правила вигляду dj→β (щоб "шматок" обов'язково закінчувався в d0) і кожне правило вигляду dj→φd0 (j≠0) замінене на dj→φ (тому що сам символ d0 буде врешті-решт на щось замінений). За припущенням індукції одержуємо, що L(Gi) множини є регулярними (i = 1,2,…f). Зазначимо, що якщо γ1',γ2',…γt' із правил d0→ γ1'di, d0→ γ2'di,…d0→γt'di та регулярна множина Ii = { γ1',γ2',…γt'}, L(Gi) і буде потрібною множиною "шматків", що починаються з di і закінчуються поверненням у d0.

Залишилося розглянути те, як може закінчитися слово після останнього "відвідування" d0. Розглянемо

граматики Gi' = <E, D\{d0}, Pi', di>. В Pi' не входять правила з K A B, а також правила вигляду dj→φd0 (ясно, що такі граматики породжують останні "шматки" ланцюжків). Знову-таки L(Gi') − регулярні, Ei = L(Gi').

Тепер зрозуміло, що кожному слову L(G) однозначно відповідає елемент регулярної множини ({α1, α2 ,

… αn} I1 I2 … If)* ∙ ({β1 , β2 , … βm } E1 E2 … Ef ) і навпаки. Теорема доведена.

83.Алгебр їчні вл стивості регулярних мов

92

Нехай Z3 - множина усіх регулярних мов в алфавіті Е. Спочатку розглянемо визначені на даній множині операції об'єднання, конкатенації й ітерації мов. Відповідно до теореми про взаємно однозначну відповідність класу регулярних мов і класу всіх регулярних множин в алфавіті Е можна говорити про те, що

ці операції дійсно визначені на множині Z3. Тоді <Z3, , ,*> - алгебра регулярних мов, що називається ще алгеброю регулярних подій. Зокрема, вона відіграє найважливішу роль в аналізі і синтезі скінчених автоматів.

Для дослідника дуже важливою проблемою є проблема оптимізації регулярних виразів за визначеними критеріями. Зручно цю проблему перевести в рамки відповідного числення і тоді одержувати нові вирази як теореми. Тоді можна говорити про формули даної алгебри (під якими розуміємо регулярні вирази).

Наступні тотожності будуть відігравати роль аксіом:

Тут , , - довільні мови носія Z3.

Можна знехтувати дужками, якщо установити порядок зв'язувань. Правила виведення:

R1 - правило заміни: нехай = і = - тотожності в алгебрі <Z3, , ,*>, причому - формула, що входить в формулу . Тоді виводимо тотожності ' = і ' = , де ' - формула, отримана заміною входження

формули в формулу на формулу .

R2 - розв‘язок рівнянь: з тотожності = виводимо тотожність = * .

Виводом назвемо послідовність тотожностей, кожна з яких є аксіомою, або отримана із попередніх за допомогою одного із правил виведення. Теорема - заключна тотожність.

Тоді основні проблеми:

-несуперечність (будь-яка теорема повинна бути тотожністю алгебри);

-повнота (будь-яка тотожність алгебри повинна бути теоремою числення).

Повнота доведена. Доведено також, що для алгебри <Z3, , ,*> не існує скінченої повної системи аксіом, якщо єдиним правилом виведення є правило заміни R1.

Несуперечність доводиться тим, що встановлюється виконання двох тверджень:

1)кожна аксіома – тотожність алгебри;

2)кожне правило виведення зберігає виконання тотожностей в алгебрі. Перше твердження очевидне.

Друге твердження для правила R1 очевидне. Залишається довести його для правила R2.

Спочатку приймемо, що тотожність = виконується в алгебрі. Застосовуючи правило заміни

послідовно до = одержимо сукупність виконуваних в алгебрі тотожностей:

= k+1 k … , k = 0,1,2,… . (1)

Таким чином, для будь-якого слова із * справедливо, що воно належить і , тобто * .

З іншого боку, нехай довільне слово довжини | | = r належить виразу , тобто . Тоді в сукупності (1) знайдеться така тотожність = r+1 r … , що r+1. А звідси r … . Тоді =

* виконується в алгебрі, тобто правило R2 зберігає виконання тотожностей в алгебрі.

84.Алгебр їчні вл стивості контекстно-вільних мов

Звичайне дослідження алгебраїчних властивостей контекстно-вільних мов пов'язують з породженням їх за допомогою алгебраїчних операцій з деякого базового класу множин.

Тому потрібно спочатку визначити ті операції, що не порушують властивостей мови бути контекстновільною. Такими, в першу чергу, є відомі нам операції об‘єднання , конкатенації , ітерації *. Але для встановлення цієї властивості на знадобляться інші важливі операції.

Визначення. Нехай L1, ..., Ln і L - контекстно-вільні мови. Суперпозицією цих мов будемо називати

тільки тоді, коли в мові L знайдеться слово ', із якого можна отримати слово шляхом заміни кожного символу ei, що міститься в , деяким словом, що належить відповідній мові Li. При цьому символ ei в різних входженнях в слово може бути замінений різними словами із відповідної мови Li.

Далі, якщо відомі про які символи ei і мови Li і L йде мова, суперпозицію будемо позначати просто Sn+1. Теорема 4.5. Клас контекстно-вільних мов замкнений щодо операції суперпозиції.

Доведення. Нехай мови Li, i = 1,2,…,n, L – довільні мови, що породжені контекстно-вільними граматиками Gi = Di, E, Pi, d0i , G = D, E, P, d0 відповідно (i = 1,2,…,n), причому не термінальні алфавіти D1, ..., Dn, D попарно не перетинаються, потужність множини терміналів E не менша n.

93

а у граматиці G – вивід d0 * '. Але тоді на основі останнього, використовуючи правила із P0, можна побудувати вивід d0 * '' у граматиці G* слова '' = x1e*1x2e*2…xne*nxn+1. Звідси, застосовуючи правила вигляду (2) множини P0, отримаємо вивід d0 *x1d01x2d02…xnd0nxn+1 у граматиці G*. Тепер, використовуючи у

граматиці G*, отримаємо вивід слова у граматиці G*,

d0 *x1d01x2d02…xnd0nxn+1 *x1y1x2d02…xnd0nxn+1 *x1y1y2d02…xnd0nxn+1 *… *x1y1x2y2… xnynxn+1. Таким

чином, має місце включення L* L(G*).

Для доведення оберненого включення виберемо довільне слово L(G*) і розглянемо вивід d0 * у граматиці G*. У зв‘язку з тим, що не термінали попарно не перетинаються, цей вивід можна перегрупувати так, що спочатку застосовуються правила із множини P0, які відповідають правилам граматики G, потім правила вигляду (2) і, насамкінець, правила із Pi, i = 1,2,…,n, у відповідному порядку. Звідси можемо

говорити, що існує слово ' = 1e1 2e2… nen n+1 L, а також слова 1 L1, ..., n Ln такі, що =

1 1 2 2… n n n+1. Отже, L* і виконується L* L(G*). Таким чином, L* = L(G*). Теорема доведена. Використовуючи результат про замкненість на множині контекстно-вільних мов, доведемо

замкненість на тій же множині і інших операцій.

Теорема 4.6. Клас контекстно-вільних мов замкнений щодо операцій , ,*.

де L1, L2 – довільні контекстно-вільні мови. Очевидно, що результатами цих суперпозицій будуть відповідно L1 L2,L1 L2, L*1. Згідно теореми 4.5 суперпозиції контекстно-вільних мов є контекстно-вільними мовами, тобто операції , ,* замкнені на множині контекстно-вільних мов. Теорема доведена.

Теорема 4.7. Клас контекстно-вільних мов не замкнений щодо операції перетину.

Доведення. Наведемо приклад не контекстно-вільного перетину двох контекстно-вільних мов. Як продемонстровано вище мова L anbncn | n 1 - не відноситься до класу контекстно-вільних мов. Однак він є результатом операції перетину двох контекстно-вільних мов

L1 ai b jc j | i, j 1 i L1 ai bic j | i, j 1 , L = L1 L2 aibici | i 1 . Теорема доведена.

Теорема 4.7. Клас контекстно-вільних мов не замкнений щодо операції доповнення. Доведення. Нехай L1 і L2 - контекстно-вільні мови. Тому що виконується над множинами умова

L1 L2 L1 L2 , то тоді зворотне припущення, що мова L1 завжди є контекстно вільною невірне тому

що L1 L2 було б завжди контекстно вільною, що суперечить теоремі 4.7.

Далі ми будемо використовувати також унарну операцію вилучення порожнього слова. Означення. Нехай L – довільна мова. Операцією вилучення порожнього слова з цієї мови будемо

називати унарну операцію (будемо позначати її del (L), яка породжує мову L' таку, що: L' = L, якщо L і L'

= L\{ }, якщо L.

Очевидно, що на множині контекстно-вільних мов ця операція замкнена.

Для контекстно-вільних граматик породження відповідної контекстно-вільної мови може бути зображений як процес розв‘язання певної системи рівнянь. Ця система рівнянь для граматики G = D, E, P, d0 визначає ту ж мову L(G) і будується наступним чином:

1) кожному не терміналу di ставимо у відповідність рівняння:

94

di ::= fi(d0,…,dn), де fi (d0,…,dn) = i1 ... ik – вираз, що складається із всіх правих частин правил вигляду

di ij P (j = 1,2,…,k);

2) граматика зображується системою

UG = {fi (d0,…,dn) | i = 0,1,2,…,n}.

Нехай система рівнянь UG = {fi (d0,…,dn) | i = 0,1,2,…,n} визначена для граматики G = D, E, P, d0 . Розглянемо процес породження мови L(G) за допомогою UG. Приймемо di = , i = 0,1,2,…,n. Тоді fi( ,…, ) = 0i, i = 0,1,2,…,n. Приймемо 0 = ( 01, ..., 0n). Потім розглянемо значення fi ( 0) = 1i, i = 0,1,2,…,n. Приймемо 1 = ( 11, ..., 1n). Рекурсивно продовживши цей процес, отримаємо k = ( k1, ..., kn), де ki = fi ( k-1),

i = 0,1,2,…,n, для будь-якого k = 1,2,… . Позначимо через i множину ki для будь-якого i = 0,1,2,…,n.

k 0

Тоді = ( 1, ..., n) називається розв‘язком системи рівнянь UG = {fi (d0,…,dn) | i = 0,1,2,…,n}, а кожен компонент i - мовою, що відповідає змінній di.

Мова, що відповідає змінній d0, називається мовою, що породжується системою рівнянь UG = {fi

(d0,…,dn) | i = 0,1,2,…,n}.

Приклад. Граматика G1 = d0, {0,1}, {d0 0d00,d0 1}, d0 і її система рівнянь

UG = {d0 ::= 0d00 1}.

Побудуємо мову, що породжується цією системою рівнянь, притримуючись наведеної рекурсивної

схеми:

0 = f( ) = 0 0 1 = 1 = 1;1 = f( 0 ) = 0( 0)0 1 = 010 1;

2 = f( 1 ) = 0( 1)0 1 = 0(010 1)0 1 = 00100 010 1;

3 = f( 2 ) = 0( 2)0 1 = 0(00100 010 1)0 1 = 0001000 00100 010 1

і т.д.

Отже, = L(G1) = {1, 010, 00100, 0001000,...}.

Граматика G2 = {d0, d1}, {0,1), {d0 d0d1,d0 0,d0 1,d1 0,d1 1}, d0 і її система рівнянь

UG = {d0 ::= d0d1 0 1, d1 ::= 0 1}.

Побудуємо мову, що породжується цією системою рівнянь, притримуючись наведеної рекурсивної схеми (самостійно).

Тепер ми можемо визначати мови за допомогою систем рівнянь (через їх розв‘язок) та відповідною граматикою. В теорії граматик рекурсивним процедурам, що породжують нескінчені контекстно-вільні мови із скінчених контекстно-вільних мов, належить важливе місце. Важливу для нас операцію рекурсії ми отримаємо, якщо приймемо замість змінних в рівняннях мови-операнди.

Нехай Un = {di ::= fi (d0,…,dn) | i = 0,1,2,…,n} система рівнянь, де fi (d0,…,dn) = di i1 ... ik – такий поліном, що кожне слово ij (1 j k) містить хоча б один нетермінал із множини D для будь-якого i = 0,1,2,…,n. Тепер будемо здійснювати наведений вище рекурсивний процес, але замість змінних d0,…,dn підставимо контекстно-вільні мови над алфавітом E.

Означення. Операцію рекурсії, задану системою рівнянь Un, визначимо як (n+1)-арну операцію Rn+1 (L1,…,Ln;L) над мовами L1,…,Ln,L, де L – мова, що одержана в результаті вилучення всіх нетерміналів із правих частин рівнянь системи Un. Операція рекурсії шляхом застосування наведеної вище рекурсивної схеми породжує нову мову L 1 = Rn+1 (L1,…,Ln;L).

Приклад. Мову, що породжується граматикою G1 попереднього прикладу, визначимо за допомогою рекурсії таким чином:

R2 (L1,L) = L(G1), схема якої визначається рівнянням d0::=d0 0d00, L1 = {1}, L= {00}.

Нехай Z2 - множина усіх контекстно-вільних мов в алфавіті Е. Розглянемо визначені на даній множині замкнені операції об'єднання, конкатенації, вилучення порожнього слова, суперпозиції та рекурсії мов. Відповідно до попередніх результатів можна говорити про те, що ці операції дійсно визначені і замкнені на

множині Z2. Тоді <Z2, , ,del,Sn+1,Rn+1> - алгебра контекстно-вільних мов. Наведемо тривіальний критерій повноти.

95

Для зручнішого описання способу функціонування автомату, зобразимо його у вигляді, наведеному на рисунку внизу. У кожний момент часу він може знаходитися лише в одному стані з множини А. У будьякий момент часу ti (i = 1,2,3,…) на вхід автомата може бути поданий будь-який вхідний символ з множини

Автомат повинен видавати на виході однозначно обумовлений функцією f2 вихідний символ і перейти в стан, обумовлений функцією f1. У момент часу ti+1 автомат готовий до появи наступного вхідного символу. Переважно будемо розглядати тільки такі автомати, для яких функції f1, f2 усюди визначені.

Загалом можна говорити і про те, чи будь-який вхідний символ може бути поданий на вхід автомата в будь-який момент часу. Якщо ця умова виконується, то будемо говорити про автомат без обмежень. Хоч можна вводити обмеження на подання символів, що розширює моделюючі можливості скінчених автоматів. Той факт, що вихід і наступний стан автомату однозначно визначаються входом і станом, дає нам право називати визначений вище скінчений автомат детермінованим. Якщо ж функції f1, f2 є відношеннями, то автомат називається недетермінованим.

Розглянуті поняття природним чином узагальнюються і на інші види автоматів. Розглянемо кілька прикладів скінчених автоматів.

Приклад 1. Нехай вхідний алфавіт Е = {1,2,3,4,5,6,7,8,9}, вихідний алфавіт B = {П,Н}, множина

Легко помітити, що цей автомат визначає парне чи непарне однорозрядне число подане на вхід і видає відповідно вихідний символ П чи Н. Очевидно, для цього автомата виконується умова f2(ei,aj) = f2(ei). Іншими словами, значення функції виходу f2 залежить тільки від входу і не залежить від стану. Такі автомати будемо називати тривіальними. Далі будемо розглядати тільки нетривіальні автомати, тобто автомати для яких виконується така умова: f2(ei,aj) f2(ei).

При описанні автомату, наведеного в прикладі, було природним задання множин переліченням, але функції f1 і f2 можна було б задати і більш наочним способом. Саме способи задання цих функцій і визначають відповідні способи задання автоматів, які ми розглянемо пізніше.

На разі ми поставимо цікаве запитання про роль, яку відіграють стани при використанні автоматів і чи потрібно їх більше одного? Адже вистачило нам одного стану у прикладі 1.

Приклад 2. Спробуємо побудувати автомат, що визначає парність багаторозрядних двійкових чисел. Тоді вхідний алфавіт E = {0,1,З}, де З - вхідний символ, після подачі якого на вхід автомат повинен видати вихідний символ П, що сигналізує про парне число на вході, чи Н, що сигналізує про непарне число на вході. Вихідний алфавіт B = {0,1,П,Н} і як би ми не намагалися обійтися одним станом нам це не вдасться. Дійсно, у момент появи символу З автоматові необхідно пам‘ятати, який же символ - парний чи непарний - був останнім на вході і тепер, відповідно, видати символ П, визначивши парне число, чи символ Н, визначивши непарне число. Тоді А = {a0,a1} і функції переходів і виходів автомата визначаються в такий спосіб:

Таким чином, введення станів визначається необхідністю моделювання пам‘яті, складною залежністю виходу від входу. Але про пам‘ять можна говорити тільки у випадку розгляду послідовності вхідних сигналів.

Зручно функціонування скінченого автомату зображувати як функціонування пристрою,

96

Рис.5.2. Загальний вигляд скінченого автомату

Вхідна і вихідна стрічки як завгодно великі, але скінчені. Керуючий пристрій (КП) може перебувати в одному станіі із визнченої їх множини. Крім того, автомат може бути реалізований і іншими способами, наприклад у вигляді нейронної мережі.

За традицією будемо називати послідовність символів алфавіту Е, яка подається на вхід автомата і цікавить користувача, - вхідною програмою. Автомат завжди знаходиться в одному стані із визначеної множини. Він зчитує перший символ програми і згідно значень функцій f1, f2 переходить у наступний стан і видає вихідний сигнал. Потім ці ж дії повторюються для другого символу вхідної програми і т.д., доки вона не закінчиться.

Приклад автомата, що описує пропускну систему метро, підкреслює корисність уявлення про автомат як про пристрій.

Приклад 3. Вхідний алфавіт Е = {е0,М,Л}, де е0 означає, що на вході пропускної системи немає людини, M означає попадання монети (жетона, картки) у прийомну кишеню, Л означає – людина на вході. Вихідний алфавіт B = {Ч,З}, де Ч означає червоне світло, З – зелене світло. Множина станів А = {a0,a1,a2} і функції переходів і виходів автомата визначаються в такий спосіб:

Стан а0 необхідний для відображення нормального стану очікування пропускного пристрою, стан а1 - для відображення стану пропускного пристрою, коли виконується спроба пройти без опускання монети, стан а2 необхідний для відображення готовності пропускного пристрою не перешкоджати проходу людини, яка оплатила проїзд. Таким чином, нам знадобилось не тільки ввести декілька станів, але й для випадку, коли в момент ti+1 на вхід автомата не потрапляє символ, ми повинні були ввести спеціальний символ для фіксації цього факту.

Варто звернути увагу, що функціонування автомату залежить від того, в якому порядку визначаються значення функцій виходу і переходів. Якщо автомат після зчитування вхідного символу спочатку формує вихідний символ за допомогою визначення функції виходу для отриманого вхідного символу і стану, в якому автомат перебував на початку такту, а потім переходить в новий стан на основі значення функції переходів, то цей автомат будемо називати автоматом Мура. Якщо автомат після зчитування вхідного символу спочатку переходить в новий стан на основі значення функції переходів, а потім формує вихідний символ на основі значення функції виходу для зчитаного вхідного символу і нового стану, то цей автомат будемо називати автоматом Мілі.

Якщо ми говоримо про вхідну програму, то аналогічно є сенс всю послідовність символів вихідного алфавіту, яку видає автомат на вихідну стрічку у відповідь на програму на вході, розглядати як результат роботи автомата над вхідною програмою і називати вихідною програмою. Саме цей факт дозволяє розглядати автомати не тільки як засіб моделювання поведінки об‘єкта керування шляхом змін його стану, але і як засіб для перетворення входу у вихід (що виправдує включення у визначення скінченого автомата функції виходів f2, тому що керування на основі стану за допомогою скінченого автомата можна було б забезпечити вже однією функцією переходів f1).

86.Способи з д ния скінчених втом тів

Наявність декількох способів задання скінчених автоматів пояснюється наявністю декількох способів задання функцій f1, f2. У прикладах 1 - 3 фактично розглянуто перший спосіб задання скінчених автоматів – аналітичний.

Більш наочним є другий спосіб задання скінченого автомата – графічний. У цьому випадку використовується орграф, що називається графом переходів чи діаграмою станів автомата. Вершини графа переходів відповідають станам, а ребра – переходам зі стану в стан. Тоді скінчений автомат із прикладу 3 можна подати у такий спосіб:

97

е0/З

Кожне ребро графа переходів позначене парою еi/bj, де еi – вхідний символ, bj – вихідний символ, визначений однозначно за допомогою функції f2(аi, еi), де аi – стан, якому відповідає вершина, з якої ребро виходить. Вершина, куди ребро заходить, визначається функцією переходів f1(аi, еi).

Однак цьому способу властиві недоліки геометричного способу задання графів. Тому використовується ще один – табличний спосіб задання скінчених автоматів. Продемонструємо вид таблиці переходів, використаної для задання функцій f1 і f2, на тому ж прикладі скінченого автомату:

Таблиця переходів містить дві підтаблиці: підтаблицю ai+1 – для задання функції f1 і підтаблицю bi – для задання функції f2. Лівий стовпець таблиці містить усі стани з множини А. Кожна з підтаблиць містить верхній рядок, у якому наведені всі символи із множини вхідних символів Е. На перетині рядка аi і стовпця еi в підтаблиці аi+1 указується значення функції переходів f1(ai,ei), а в підтаблиці bi – значення функції виходу f2(ai,ei).

87.Проблеми дослідження втом тів

Розглянуті вище визначення, способи задання і приклади скінчених автоматів дозволяють зробити, можливо, поки ще недостатньо визначений, висновок про скінчений автомат як математичний об‘єкт для моделювання об‘єктів, явищ і процесів навколишнього світу, що вимагають обліку їхнього стану при погодженні виходу з входом. Таким чином, з огляду на виражувальні можливості скінчені автомати перевершують уже відомі нам математичні засоби, наприклад, графи і відношення. Уже той факт, що граф використовується для подання скінченого автомату, але ще не представляє увесь скінчений автомат і його спосіб функціонування, підтверджує зроблений висновок.

Але більш широкі виражувальні можливості скінчених автоматів роблять більш серйозною проблему їхнього дослідження, що необхідно для реалізації одного з фундаментальних підходів кібернетики

– модельного підходу, згідно з яким проблеми управління об‘єктами, явищами і процесами навколишнього світу повинні вирішуватися на основі вирішення аналогічних проблем дослідження моделей. Автомат, зокрема скінчений автомат, є дуже розповсюдженою моделлю. Сформулюємо ряд проблем дослідження скінчених автоматів, виходячи з проблем аналізу реальних об‘єктів управління.

Отже, скінчений автомат у процесі функціонування, зчитуючи програму, друкує вихідну послідовність символів відповідно до функцій f1, f2. Якщо припустити, що автомат описує функціонування комп‘ютера, то нас з точки зору перевірки правильності обчислень цікавить вихідна послідовність автомата для кожної програми. Тоді, порівнявши її з перевіреною іншим чином правильною вихідною послідовністю

R*- множина вихідних послідовностей в алфавіті В.

Таким чином, нами сформульована задача аналізу автомата.

Якщо ми проектуємо комп‘ютер, то згадане відображення повинне бути відомим заздалегідь. Тоді стоїть задача знайти автомат, що задає це відображення. Іншими словами, стоїть задача знайти автомат, якщо задане відображення

Таким чином, нами сформульована задача синтезу автомата.

98

Очевидно, що відображення (5.5) і (5.6) задані на різних множинах. Адже якщо автомат заданий, то відома множина його станів, і ми повинні установити вихідну послідовність для кожної програми при будьякому стані на початок роботи. При синтезі ми не знаємо заздалегідь станів, і відображення задається без їхнього обліку.

Реакція нетривіального автомата М на визначені впливи не передбачувана, якщо стан М невідомий. З іншого боку, ця реакція завжди може бути передбачена, якщо початковий стан відомий. Таким чином, одна з основних задач аналізу скінчених автоматів полягає в тому, щоб розпізнати стан досліджуваного автомата. Після того як стан розпізнаний, можна визначити поведінку автомата при всіх подальших впливах на нього і можуть бути зроблені кроки для переведення автомата в певні стани (режими роботи об‘єкта, що моделюється автоматом), бажані для дослідника. Цю задачу називають задачею розпізнавання станів.

Наша наступна мета – розглянути засоби і методи вирішення цих задач. Почнемо з задачі аналізу. Слід зазначити, що існує ціла низка більш дрібних задач, вирішення яких або дозволяє глибше пізнати основні властивості автоматів, або лягає в основу вирішення основних задач.

Очевидно, задачу аналізу скінченого автомата можна розбити на два етапи:

для довільного слова з множині E* визначити, чи переглядається вона автоматом (адже автомат може зупинитися, не переглянувши слово, чи виникнуть інші неприємні ситуації);

якщо слово переглядається автоматом, то визначити слово з множини B*, яке скінчений автомат видає на виході, якщо на його вхід подане слово .

Очевидно, якщо розглядати проблему аналізу в такому плані, то дуже важливо враховувати стан автомата. Наприклад, нехай автомат заданий таким графом переходів

Вхідна програма 0111 буде переглянута автоматом у випадку, якщо він на момент подачі першого її символу знаходився у стані a0. Але якщо автомат знаходився у стані a1 , то він зупиниться і не перегляне

слово 0110. З іншого боку, якщо автомат знаходився у стані a0, то він перегляне слово 0111 і по закінченні його буде знаходитися в стані a1, причому на виході для слова 0111 з‘явиться слово 0000. Якщо ж на вхід подати слово 011120, то автомат по закінченні слова перейде в стан a3, а на виході з‘явиться слово 000021.

Отже, щоб однозначно визначити ті слова, що автоматом переглядаються, необхідно обумовити:

3)стан автомата, у якому він повинен розпочинати перегляд вхідних програм (назвемо цей стан - початковим);

4)стани, в одному з яких повинен виявитися автомат після закінчення вхідної програми (назвемо їх

заключними станами).

Будемо говорити, що вхідна програма розпізнається скінченим автоматам, якщо, починаючи з

першого символу вхідної програми і початкового стану, автомат, відповідно до функції f1, буде переходити зі стану в стан і по закінченні вхідної програми виявиться в одному із заключних станів. Очевидно, що для недетермінованого автомата умови розпізнавання вхідної програми скінченим автоматам змінюються. У цьому випадку приймаються до уваги всі можливі варіанти переходів автомату із стану в стан згідно з відношенням f1. Вхідна програма розпізнається автоматом, якщо, починаючи з першого символу вхідної програми і початкового стану, існує варіант переходів автомата згідно з відношенням f1, при якому автомат по закінченні вхідної програми виявиться в одному із заключних станів.

Доведено, що для детермінованого скінченого автомата М, що розпізнає мову L(M), існує недетермінований автомат M‘ такий, що мова, яка розпізнається ним, L(M‘) = L(M). Але загалом клас мов, які розпізнаються детермінованими скінченими автоматами, є власною підмножиною класу мов, які розпізнаються недетермінованими скінченими автоматами.

Очевидно, перший етап задачі аналізу пов‘язаний із завданням мови шляхом розпізнавання її ланцюжків автоматом. Розглянемо більш докладно цю проблему.

88.Регулярні мови т скінчені втом ти

Отже, за визначенням, вхідна програма розпізнається скінченим автоматом, якщо скінчена послідовність символів вхідної програми переводить автомат з початкового стану в один із заключних станів (відповідно до функції переходів f1).

Для скінченого автомата М серед множини його станів А виділимо початковий стан a0 і підмножину заключних станів A0. Тоді для скінченого автомата М можна говорити про множину слів у алфавіті Е, які розпізнаються цим автоматом. Позначимо її L(M). Говорять, що мова L(M) задається автоматом М. Вірніше

99

варто говорити не про скінчений автомат М = E,A,B,f1,f2 , а про скінчений розпізнавач М = E,A,f1,a0,A0 , де a0 - початковий стан, A0 A - підмножина заключних станів.

Як же пов‘язані множини слів, що розпізнаються автоматами, і мови типів 0, 1, 2, 3? Нехай, наприклад, задані такі мови:

L1 = { ,0,1,01,10, 000, 001, 010, 011, 100, 110, 101, 111}; L2 = {0,00,000,...};

L3 = {01,0011,000111,...}.

Зробимо спробу задати ці мови за допомогою скінчених розпізнавачів. Це досить легко зробити з мовами L1 – L2, задавши відповідні розпізнавані графами переходів:

Але всі наші спроби побудувати скінчений розпізнавач для мови L3 не принесуть позитивного результату. Для обґрунтування цього висновку сформулюємо і доведемо теорему.

Теорема 5.1. Мова розпізнається скінченим розпізнавачем тоді і тільки тоді, коли вона є регулярною.

Доведення.

а) необхідність. Нехай L = L(M) для скінченого автомата M. Покажемо, що L -регулярна множина. Для цього побудуємо автоматну граматику G = A,E,P,d0 , де

d0 = a0 - початковий стан;

А - множина станів скінченого автомата M;

Р – множина правил виведення, обумовлена в такий спосіб: якщо f1(ai,ej) = al, то ai ejal Р, причому якщо ai - заключний стан, то додаємо до P правило ai .

Далі індукцією покажемо, що кожен крок виведення в граматиці G імітує такт функціонування автомата M, тобто покажемо, що

ai G для ai A,

причому у виводі k+1 слів тоді і тільки тоді, коли автомат за k тактів переходить з (ai, ) у (aj, ), де aj - один із заключних станів.

Крок 1. k =0 і щоб i G потрібно щоб автомат не зробив жодного кроку.

Крок 2. Нехай теорема виконується для слів довжини k. Покажемо, що вона виконується для слів

довжини k+1. Для такого слова це означає, що ai G0 , причому = ei , де = k, може бути тільки якщо i G ei i = k.

б) достатність. Нехай L - регулярна множина. Покажемо, що L = L(M) для деякого скінченого автомата M.

Якщо L - регулярна множина, то існує автоматна граматика G = A,E,P,d0 , правила виведення якої мають вигляд ai ejal або ai ej, така що L = L(G).

Для доведення побудуємо на основі автоматної граматики G = A,E,P,d0 скінчений розпізнавач М =E,A,f1,a0,A0 , де a0 = d0 - початковий стан; А - множина станів скінченого розпізнавача M; A0 A - підмножина заключних станів; функція переходів f1 формується на основі множини правил виведення Р в

такий спосіб: якщо ai ejal Р, то f1(ai,ej) = al, якщо ai ej Р, то f1(ai,ej) = al, де al - заключний стан, якщо aiР, то ai - заключний стан.

Далі легко індукцією показати, що кожен такт автомата М імітує крок виведення в граматиці G , тобто покажемо, що

ai G для ai A,

причому автомат за k тактів переходить з конфігурації (ai, ) у конфігурацію (aj, ), де aj - один із заключних станів тоді і тільки тоді, коли у виводі k+1 слів. Теорема доведена.

89.Ан ліз втом тів

Назвемо стан автомата в початковий момент часу початковим. Зазначимо, що задання автомата й опис його функціонування обумовлюють появу на виході послідовності тієї ж довжини, що і довжина програми. Довжиною послідовності назвемо кількість символів послідовності.

Якщо відомо початковий стан a0, то функції f1 і f2 дозволяють побудувати вихідну послідовність довжини k для довільної програми ei1,ei2,…,eik. Дійсно, якщо k - 1, то оскільки f1 і f2 усюди визначені, ми визначимо наступний стан al1 і вихідний символ bj1.

100