
chap_0
.pdf
6.3. ЗАДАЧI РОЗДIЛУ |
63 |
6.3Задачi роздiлу
6.1. В урну, яка мiстить двi кулi, поклали бiлу кулю, пiсля чого з неї навмання вийняли одну кулю. Знайти ймовiрнiсть того, що вийнята куля виявиться бiлою, якщо рiвноможливi усi припущення про початковий склад куль в урнi (кiлькiсть бiлих та чорних). Розв’язання. Нехай подiя A – вийнята з урни куля є бiлою. Можливi такi припущення (гiпотези) про початковий склад куль в урнi: H1 – бiлих куль немає, H2 – одна бiла куля, H3 – двi бiлi кулi. Оскiльки усi три гiпотези рiвноймовiрнi, то p(H1) = p(H2) = p(H3). Крiм того, цi гiпотези утворюють повну групу подiй, тому p(H1)+p(H2)+p(H3) = 1. Таким чином, p(H1) = p(H2) = p(H3) = 1=3.
Iмовiрнiсть вийняти бiлу кулю за умови, що спочатку в урнi не було бiлих куль, p(A=H1) = 1=3. Iмовiрнiсть вийняти бiлу кулю за умови, що спочатку в урнi була одна бiла куля, p(A=H2) = 2=3. Iмовiрнiсть вийняти бiлу кулю за умови, що спочатку в урнi були двi бiлi кулi, p(A=H3) = 3=3 = 1. За формулою повної iмовiрностi
p(A) = p(H1)p(A=H1) + p(H2)p(A=H2) + p(H3)p(A=H3)
обчислимо ймовiрнiсть шуканої подiї
p(A) = 13 13 + 13 23 + 13 1 = 23:
6.2. Турист навмання вийшов iз мiста А у мiсто Б ( рис. 6.1). Яка ймовiрнiсть того, що вiн прийде у мiсто Б?
Вiдповiдь. 11=18.
6.3. В урну, яка мiстить n куль, поклали бiлу кулю, пiсля чого з неї навмання вийняли одну кулю. Знайти ймовiрнiсть того, що вийнята куля виявиться бiлою, якщо рiвноможливi усi припущення про початковий склад куль в урнi (кiлькiсть бiлих та чорних).
Вiдповiдь. 2nn+2+2 .
6.4. У пiрамiдi п’ять гвинтiвок, три з яких мають оптичний прицiл. Iмовiрнiсть того, що стрiлець влучить у мiшень при пострiлi з гвинтiвки з оптичним прицiлом, дорiвнює 0,95; для гвинтiвки без

64 |
РОЗДIЛ 6. ФОРМУЛA ПОВНОЇ ЙМОВIРНОСТI |
À
Á
Рис. 6.1. Яка ймовiрнiсть, що турист попаде з А у Б?
оптичного прицiлу ця ймовiрнiсть дорiвнює 0,7. Знайти ймовiрнiсть того, що мiшень буде уражена, якщо стрiлець зробить один пострiл з гвинтiвки, яку вiн узяв з пiрамiди навмання.
Вiдповiдь. 0; 85.
6.5. В першiй урнi мiститься 10 куль, з них 8 бiлих, в другiй – 20 куль, з яких 4 бiлi. З кожної урни навмання вийняли по однiй кулi, а потiм iз цих двох куль навмання взяли одну кулю. Знайти ймовiрнiсть того, що взята бiла куля.
Вiдповiдь. 0; 5.
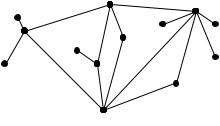
6.6. Турист на кожному роздорiжжi вибирає подальший напрямок руху навмання (див. рис. 6.2). Яка ймовiрнiсть того, що турист попаде з пункту А у пункт Б?
Вiдповiдь. 67=120.
6.7. У кожнiй з трьох урн мiститься по 6 чорних та по 4 бiлi кулi. З першої урни навмання вийнята одна куля i перекладена в другу урну, пiсля чого з другої урни навмання вийнята одна куля i перекладена в третю урну. Знайти ймовiрнiсть того, що куля, яка навмання вийнята з третьої урни, виявиться бiлою.
Вiдповiдь. 0; 4.
6.8. Перед iспитом студент вивчив лише 16 бiлетiв з 30. Як йому доцiльнiше брати бiлет – першим, другим чи третiм?
Вiдповiдь. Iмовiрнiсть взяти бажаний бiлет не залежить вiд того брати його першим, другим або третiм. Ця ймовiрнiсть дорiвнює вiдношенню числа вивчених бiлетiв до числа всiх бiлетiв.
6.3. ЗАДАЧI РОЗДIЛУ |
65 |
6.9. У пiрамiдi десять гвинтiвок, чотири з яких мають оптичний прицiл. Iмовiрнiсть того, що стрiлець влучить у мiшень при пострiлi з гвинтiвки з оптичним прицiлом, дорiвнює 0,95; для гвинтiвки без оптичного прицiлу ця ймовiрнiсть дорiвнює 0,8. Стрiлець влучив у мiшень iз гвинтiвки, яку взяв iз пiрамiди навмання. Що бiльш ймовiрно: пострiл був зроблений iз гвинтiвки з оптичним прицiлом чи без нього? Вiдповiдь. Бiльш ймовiрно, що гвинтiвка була без
оптичного прицiлу (24=43 > 19=43).
6.10. Кiлькiсть вантажних автомашин, що їдуть по шосе, на якому стоїть бензоколонка, вiдноситься до кiлькостi легкових автомашин, що їдуть по тому ж шосе, як три до двох. Ймовiрнiсть того, що буде заправлятися вантажна автомашина, дорiвнює 0; 1, для легкової така ймовiрнiсть дорiвнює 0; 2. До бензоколонки пiд’- їхала для заправки автомашина. Знайти ймовiрнiсть того, що це вантажiвка.
Вiдповiдь. 3=7.
6.11.Вирiб перевiряється на стандартнiсть одним iз двох товарознавцiв. Iмовiрнiсть того, що вирiб попаде до першого товарознавця, дорiвнює 0,55, а до другого – 0,45. Iмовiрнiсть того, що стандартний вирiб буде визнаний стандартним першим товарознавцем, дорiвнює 0,9; а другим, – 0,98. Стандартний вирiб при перевiрцi було визнано стандартним. Знайти iмовiрнiсть того, що цей вирiб перевiряв другий товарознавець. Вiдповiдь. 0; 47.
6.12.Три стрiльцi зробили залп, причому двi кулi влучили у мiшень. Знайти ймовiрнiсть того, що третiй стрiлець влучив у мiшень, якщо ймовiрностi влучення у мiшень першим, другим та третiм стрiльцями вiдповiдно дорiвнюють 0,6; 0,5 та 0,4.
Вiдповiдь. 10=19.
6.13. Турист прийшов iз пункту A у пункт Б (рис. 6.2). Яка ймовiрнiсть того, що вiн пройшов по маршруту AВБ?
Вiдповiдь. 12=67.
6.14. В урнi n куль. Усi можливi припущення про число бiлих куль в урнi рiвноможливi. Навмання з урни беруть одну кулю. Яка ймовiрнiсть того, що ця куля бiла?
66 |
РОЗДIЛ 6. ФОРМУЛA ПОВНОЇ ЙМОВIРНОСТI |
À
Â
Á |
Рис. 6.2. Яка ймовiрнiсть, що турист пройде по маршруту АВБ ?
Вiдповiдь. Hi – гiпотеза, що в урнi рiвно i бiлих куль.
n |
|
n |
+ n |
+ : : : + n |
= |
2 : |
|
p = i=0 p(Hi)p(A=Hi) = n + 1 |
|||||||
X |
1 |
1 |
|
2 |
n |
|
1 |
6.15. У двох урнах знаходиться вiдповiдно n1 i n2 куль, iз них бiлих куль m1 та m2. З першої урни переклали в другу урну одну кулю, колiр якої невiдомий. Пiсля цього з другої урни беруть одну кулю. Яка ймовiрнiсть того, що ця куля бiла?
Вiдповiдь. A – iз другої урни взяли бiлу кулю. H1 – iз першої урни переклали в другу бiлу кулю. H2 – iз першої урни переклали в другу не бiлу кулю.
|
m1 |
m1 |
|
|
p(H1) = |
|
; p(H2) = 1 |
|
; |
n1 |
n1 |
|||
p(A) = p(H1)p(A=H1) + p(H2)p(A=H2) =
= |
m1 m2 + 1 |
+ 1 |
m1 |
|
m2 |
= |
m1 + n1m2 |
: |
||
|
|
|
|
|
|
|
||||
n1 n2 + 1 |
n1 |
|
n2 + 1 |
n1(n2 + 1) |
||||||
6.16. Прилад складається з n блокiв, якi дублюють один одного, i може працювати в одному з двох режимiв – сприятливому або несприятливому. В сприятливому режимi надiйнiсть роботи кожного блоку дорiвнює p1, а в несприятливому – p2. мовiрнiсть того, що прилад працюватиме в сприятливому режимi дорiвнює p, в несприятливому – (1 p). Обчислити надiйнiсть приладу.
Вiдповiдь. A – прилад надiйний. H1 – прилад працює в сприятливому режимi. H2 – прилад працює в несприятливому режимi.
p(A) = p(H1)p(A=H1) + p(H2)p(A=H2) =
= p(1 (1 p1)n) + (1 p)(1 (1 p2)n):

6.3. ЗАДАЧI РОЗДIЛУ |
67 |
6.17. В урну, яка мiстить n куль, поклали бiлу кулю. Яка ймовiрнiсть того, що взята з урни куля буде бiла, якщо всi припущення про початковий склад бiлих куль рiвноможливi?
Вiдповiдь. A – взята куля – бiла. Hi(i = 0; 1; 2; : : : ; n) – гiпотеза, що
спочатку |
в |
урнi було рiвно |
|
|
n |
|||||
i бiлих куль. p = Pi=0 p(Hi)p(A=Hi) = |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
+ |
2 |
+ : : : + n+1 |
= |
|
n+2 |
: |
|
n+1 |
n+1 |
|
n+1 |
n+1 |
|
|
2(n+1) |
|
|
6.18. Стрiлець A влучає в мiшень з iмовiрнiстю p1 = 0; 6, стрiлець B – з iмовiрнiстю p2 = 0; 5, а стрiлець C – з iмовiрнiстю p3 = 0; 4. Стрiльцi зробили залп по мiшенi. Вiдомо, що є два влучення. Що бiльш iмовiрно: попав C у мiшень чи нi?
Вiдповiдь. A – подiя, що в мiшень попали 2 кулi. H1 – гiпотеза, що С влучив у мiшень. H2 – гiпотеза, що С не влучив у мiшень.
p(A) = p(H1)p(A=H1) + p(H2)p(A=H2) =
=0; 4(0; 6 0; 5 + 0; 4 0; 5) + 0; 6 0; 6 0; 5 =
=0; 2 + 0; 18 = 0; 38;
p(H1=A) = |
p(H1) p(A=H1) |
= |
0; 2 |
|
|
0; 53; |
|
0; 38 |
|||||||
|
p(A) |
|
|
||||
p(H2=A) = |
p(H2) p(A=H2) |
= |
0; 18 |
|
0; 47: |
||
|
|
||||||
0; 38 |
|||||||
|
p(A) |
|
|
||||
6.19. На вхiд радiолокацiйного пристрою надходять: з iмовiрнiстю p – сигнал iз шумом i з iмовiрнiстю (1 p) – тiльки шум. Якщо надходить сигнал iз шумом, то пристрiй реєструє наявнiсть сигналу з iмовiрнiстю p1, якщо надходить тiльки шум, то пристрiй реєструє наявнiсть сигналу з iмовiрнiстю p2. Вiдомо, що пристрiй зареєстрував сигнал. Яка iмовiрнiсть, що сигнал надiйшов iз шумом?
Вiдповiдь. A – прилад зареєстрував сигнал. H1 – гiпотеза, що надiйшов сигнал iз шумом. H2 – гiпотеза, що надiйшов лише шум.
p(A) = p(H1)p(A=H1) + p(H2)p(A=H2) = pp1 + (1 p)p2;
p(H1=A) = |
p(H1)p(A=H1) |
= |
pp1 |
: |
|
p(A) |
pp1 + (1 p)p2 |
||||
|
|
|
6.20. Три мисливцi одночасно вистрiлили у вовка. Вовка вбито однiєю кулею. Яка ймовiрнiсть того, що вовк убитий першим, дру-

68 |
РОЗДIЛ 6. ФОРМУЛA ПОВНОЇ ЙМОВIРНОСТI |
гим або третiм мисливцем, якщо ймовiрностi влучення для них
дорiвнюють вiдповiдно p1 = 0; 2; p2 = 0; 4; p3 = 0; 6.
Вiдповiдь. A – вовка вбито однiєю кулею. H1 – вовка вбито першим мисливцем. H2 – вовка вбито другим мисливцем. H3 – вовка вбито третiм мисливцем.
p(A) = p(H1)p(A=H1) + p(H1)p(A=H1) =
=0; 2 0; 6 0; 4 + 0; 8(0; 4 0; 4 + 0; 6 0; 6) =
=0; 048 + 0; 416 = 0; 464;
p(H1=A) = p(H1)p(A=H1) = 0; 048 = 0; 10: p(A) 0; 464
6.21. Деталi виробляються на двох заводах. Об’єм продукцiї другого заводу в n раз перевищує об’єм продукцiї першого заводу. Частка браку на першому заводi – p1, на другому – p2. Навмання взята деталь виявилася бракованою. Яка ймовiрнiсть того, що вона випущена другим заводом?
Вiдповiдь. A – деталь бракована. H1 – гiпотеза, що деталь виготовлена першим заводом. H2 – гiпотеза, що деталь виготовлена другим заводом.
p(A) = p(H1)p(A=H1) + p(H2)p(A=H2) = |
p1 |
+ |
n |
p2; |
|||||||
n + 1 |
n + 1 |
||||||||||
|
|
|
|
|
|
|
|
|
|||
p(H2=A) = |
p(H2)p(A=H2) |
= |
|
np2 |
: |
|
|
|
|
||
p(A) |
|
|
|
|
|
|
|
||||
|
|
np2 + p1 |
|
|
|
|
|||||
Роздiл 7
Схема Бернуллi
7.1Короткi теоретичнi вiдомостi
Припустимо, що проводяться n незалежних дослiдiв, в кожному з яких iз однiєю i тiєю ж ймовiрнiстю p може наступити деяка подiя A. Яка ймовiрнiсть того, що в n дослiдах подiя A наступить рiвно k (0 k n) разiв? Вiдповiдь на це питання дає формула Бернуллi
Pn(k) = Cnkpkqn k; |
(7.1) |
де Cnk – число сполук iз n елементiв по k, q = 1 p. Числа Pn(k) називаються бiномними ймовiрностями.
Найiмовiрнiше число успiхiв. Серед чисел Pn(0), Pn(1),
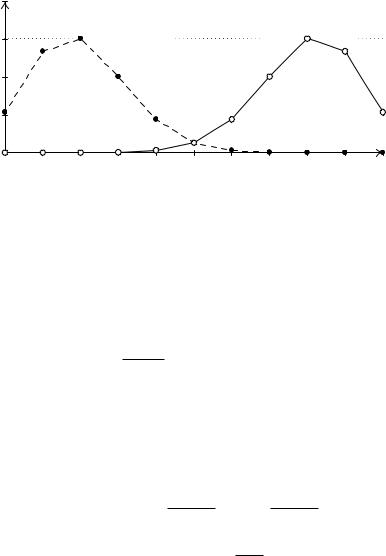
Pn(2),. . . , Pn(n) виберемо найбiльше. Число k0 (0 k0 n), при якому ймовiрнiсть Pn(k0) найбiльша, називається найбiльш iмовiрним (найiмовiрнiшим) числом успiхiв. Рис. 7.1 дає геометричну iлюстрацiю найбiльш iмовiрного числа успiхiв.
Теорема 7.1. Якщо число = np q не цiле, то найбiльш iмовiрне число успiхiв дорiвнює найближчому до справа цiлому числу. Якщо число цiле, то найбiльш iмовiрне число успiхiв має два значення: i + 1:
Середнє число успiхiв. Число np iнтерпретують як середнє число успiхiв у n дослiдах.
69
70 |
РОЗДIЛ 7. СХЕМА БЕРНУЛЛI |
0:4 |
|
a) |
b) |
0:2 |
|
0 |
2 |
4 |
6 |
8 |
k |
Рис. 7.1. a) графiк P10(k) для p = 0; 2; k0 = 2. b) графiк P10(k) для p = 0; 8; k0 = 8
Теорема 7.2 (Локальна теорема Лапласа). При великих n i не дуже близьких до нуля й одиницi значень p справедлива наближена рiвнiсть
|
|
|
|
|
|
1 |
|
|
|
|
(7.2) |
||
|
|
|
|
|
Pn(k) ' p |
|
|
|
'(x); |
||||
|
|
|
|
|
npq |
||||||||
де |
x = |
k np |
; '(x) = |
|
1 |
e |
x2 |
: |
|
||||
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|||||||
|
p |
npq |
|
|
p2 |
|
|
|
|
||||
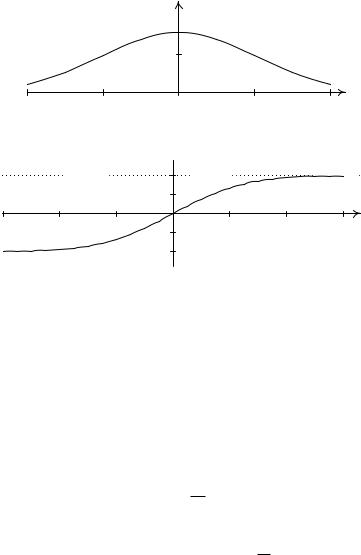
Удодатках на с. 243 подана таблиця Е.1 значень функцiї '(x),
ана рис. 7.2 зображений графiк цiєї функцiї.
Теорема 7.3 (Iнтегральна теорема Лапласа). При великих n i не дуже близьких до нуля й одиницi значень p справедлива наближена рiвнiсть
|
1 |
|
|
|
2 |
|
|
pnpq |
|
|
|
pnpq |
|
|
(7.3) |
||||
p(k |
|
|
k |
|
k |
) |
|
|
k2 np |
|
|
|
|
k1 np |
|
; |
|
||
|
|
|
де |
|
(x) = Z x '(t)dt = |
p |
1 |
Z x e t22 dt: |
|
||||||||||
|
|
|
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
||
Формули (7.2) та (7.3) можуть зводити складнi обчислення бiномних ймовiрностей (7.1) до порiвняно простих обчислень. Для того щоб похибка цих наближених рiвностей була незначною, потрiбно щоб добуток npq був бiльший 10.
7.1. КОРОТКI ТЕОРЕТИЧНI ВIДОМОСТI |
71 |
p
































 0:5
0:5










































0:25
2 |
1 |
0 |
1 |
2 x |
Рис. 7.2. Графiк функцiї '(x)
0:5 
2 |
1 |
0 |
1 |
2 |
3 x |
0:5
Рис. 7.3. Графiк функцiї (x)
На с. 244 подана таблиця Е.2 значень функцiї (x). На рис. 7.3 зображений графiк цiєї функцiї.
Коли одна з величин p або q близька до нуля, то формулами (7.2) та (7.3) доцiльнiше не користуватися. Для цього випадку iснує бiльш точна формула Пуассона.
Теорема 7.4 (Формула Пуассона). При великих n i малих p справедлива наближена рiвнiсть
k |
|
Pn(k) k! e ; |
(7.4) |
де = np – середнє число успiхiв.
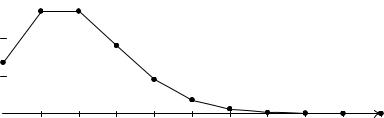
На рис. 7.4 зображений графiк функцiї kk! e для = 2. Для того щоб похибка цiєї наближеної рiвностi була незна-
чною, n має бути не меншим кiлькох десяткiв, а добуток np лежати в межах вiд 1 до 10.
Звернемо увагу на одну властивiсть формули (7.4). Для обчислення певного числа успiхiв необов’язково знати значення n та
72 |
РОЗДIЛ 7. СХЕМА БЕРНУЛЛI |
0:3 
0:2
0:1
0 |
2 |
4 |
6 |
8 |
k |
Рис. 7.4. Графiк функцiї k e
k!
p. Усе визначається числом = np, яке служить середнiм числом успiхiв.
Формула Пуассона застосовується для знаходження ймовiрностей рiдкiсних подiй. Приклади таких подiй неважко назвати: народження близнюкiв, досягнення 100-лiтнього вiку, аварiя на мiському транспортi, помилки та дефекти у пiдручниках i т.д.
7.2Контрольнi питання
1.Який змiст вкладається в поняття "серiя незалежних випробувань"?
2.Що таке схема Бернуллi?
Pn
3. Як довести рiвнiсть k=0 Pn(k) = 1?
4.Як знайти найiмовiрнiше число появ випадкової подiї у серiї незалежних випробувань?
5.У яких межах може лежати найiмовiрнiше число успiхiв?
6.Чи однозначно визначається найiмовiрнiше число успiхiв?
7.Дайте практичне тлумачення числа np як середнього числа успiхiв.
8.За якою формулою можна знайти ймовiрнiсть рiдкiсного явища?
9.За яких умов слiд застосувати локальну, а за яких – iнтегральну формулу Лапласа?
10.За яких умов слiд застосовувати формулу Пуассона, а за яких – формули Лапласа?
