1 Електродинамiка
1Електродинамiка
Електродинамiкою називають роздiл фiзики, в якому вивчають вза¹модiю мiж зарядженими тiлами.
Вза¹модi¨ стосуються вза¹модiй мiж електронами та ядрами в атомах та молекулах. Також електромагнiтну природу мають пружнi сили (тертя та iншi).
Електродинамiка лежить в основi електротехнiчних дисциплiн, теорi¨ електричних кiл тощо.
Електромагнiтнi явища ¹ наслiдком набування тiлами електричних зарядiв. Ця вза¹модiя проявля¹ться у випадку нерухомих зарядiв (електростатика), а також для рухомих зарядiв (магнетизм).
Здавалося б, що цi два прояви вза¹модi¨ не узгоджуються з принципом вiдносностi. Теорiя Максвела пов'язу¹ електри- чне та магнiтне поля i узгоджу¹ принцип вiдносностi щодо електромагнiтних вза¹модiй
1.1Електичний заряд
Електричного заряду тiла набувають внаслiдок електризацi¨. Наприклад, при дотику ебонiт-шерсть, скло-шовк. При вза¹модi¨ двох електризованих ебонiтових паличок виникаютиме сила вiдштовхування (2 склянi палички аналогiчно). Скляна i ебонiтовапритягування
Знак сили (вiдштовх. чи притягання) означа¹, що електричнi заряди можуть бути двох знакiв - вiд'¹мнi та додатнi (однойменного вiдштовхуються, рiзнойменного притягуються)
Атоми складаються з ядер, навколо яких ¹ електрони. Прийнято вважати, що заряд електрона - вiд'¹мний, ядер додатнiй. Ядра складаються з протонiв, кiлькiсть яких дорiвню¹ кiлькостi електронiв, заряд протона дорiвню¹ заряду електрона, та ма¹ iнший знак
Всi атоми електронейтральнi ) величина заряду не залежить вiд швидкостi.
Виходячи з тако¨ будови атому, електризацiю речовини можна пояснити змiною кiлькостi електронiв в нiй. Якщо при електризацi¨ тiло набува¹ додатньо¨ кiлькостi електронiв, то воно матиме вiд'¹мний заряд. q = Ne , e = 1:6 10 19 Êë
I навпаки, заряд буде додатнiй при вiддаваннi електрона. q = Ne
Вважа¹ться, що електрон не ма¹ просторово¨ структури розподiлу власного заряду - заряд електрона зосереджений в точцi. Це положення протирiчить фундаментальним поняттям, бо в такому випадку енергiя електрона повинна бути безкiнечною. Але в той час me = 9:1 10 31êã
У протона заряд ма¹ просторовий розподiл. Дослiди показують, що весь заряд протона зосереджений на вiдстанi 10 15 ì вiд центра протона.
dr - товщина сферичного шару
(~r)-об'¹мна густина заряду
Площа зазначено¨ фiгури ма¹ бути рiвною елементарному заряду. Оскiльки заряд e - елементарний
i менше заряду нема¹, то звiдки з'явля¹ться (~r) - об'¹мна густина заряду?
Для пояснення цього факту була запропонована гiпотеза про iснування кваркiв. Вважа¹ться, що протон склада¹ться з 3 кваркiв
Це означа¹, що припускають, що цi кварки рухаються хаотично по об'¹му протона.
e я |
e |
dr |
|
|
|
|
|||
e |
1.01 |
1.03 |
1.04 |
|
1.02 |
||||
|
1
1.2 Закон збереження заряду. |
1 Електродинамiка |
1.2Закон збереження заряду.
При електризацi¨ вiдбува¹ться перехiд певно¨ кiлькостi електронiв.
Електрон - це стiйка частинка з нескiнченним часом життя, як i протони. Через це заряд будь-яко¨ системи електричних тiл ма¹ зберiгатися за умови, що система замкнута (закон збереження заряду)
Ìà¹ìî, ùî P |
P |
qi = const ; qi = qïîâí ; qïîâí = const .
ii
Закон збереження заряду ма¹ бiльш фундаментальне трактування. Вiн також вплива¹ на процеси перетворення елементарних частинок з утворенням нових заряджених частинок.
Наприклад, при -розпадi утворюються електрон, а заряд ядра збiльшу¹ться на e.
1.3Закон Кулона
Закон Кулона визнача¹ вза¹модiю мiж точковими нерухомими зарядами. Рис 1.5 Точковими називаються заряди, розмiри яких багато меншi за вiдстань до iнших об'¹ктiв.
Fêë = 1 jq1jjq2j
4 0 r2
"0 = 8:85 10 12 Ô
ì
Запишемо формулу закону Кулона у векторному виглядi
~ |
|
|
1 q1q2 ~r12 |
~ |
|
1 q1q2 ~r21 |
|||||||||
F12 |
= |
|
|
|
|
|
|
|
F21 |
= |
|
|
|
|
|
|
4 "0 j~r12j2 j~r12j ; |
4 "0 j~r21j2 j~r21j |
|||||||||||||
~r12 = ~r21 |
|
|
|
|
|
|
|
||||||||
~ |
= |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
F12 |
F21 |
|
|
|
|
|
|
|
|||||||
До яких вiдстаней викону¹ться закон Кулона? Закон Кулона викону¹ться для r > 10 15ì
Вза¹модiю мiж зарядами здiйснюють шляхом обмiну вiртуальними фотонами. Очевидно, що max m(довжина хвилi прита- манна фотонам, макс.) ма¹ дати верхню межу, для яко¨ викону¹ться закон Кулона.
107мзакон Кулона ще викону¹ться. |
|
|
min 8 Ãö òà rmax |
Найменша частота електромагнiтно¨ хвилi, що спостерiга¹ться в природi ¹ хвиля Шумана. Для |
|
||
+ |
+ |
|
|
|
|
q<0 |
|
|
|
qпр |
|
+ |
- |
q>0 |
|
q |
|
||
|
|
|
|
|
1.05 |
1.06 |
|
1.4Напруженiсть електричного поля.
Електростатичне поле ма¹ польову природу.
Заряд в оточуючому просторi створю¹ електричне поле, а це поле чинить дiю на iнший заряд. Вiдповiдно iнший заряд створю¹ сво¹ поле, що чинить силову дiю на перший заряд. На заряди силову дiю чинять електричнi поля.
Для означення вводять вектор напруженостi електричного поля. Визнача¹мо його з формули ~ |
~ |
|
F |
||
|
E = |
qïðîá |
~ |
|
|
F - ñèëà, ç ÿêîþ ïîëå äi¹ íà qïðîá. |
|
|
|
~ |
|
qïðîá > 0; qïðîá ма¹ бути достатнiм, щоб вимагати силу F , але таким, щоб не створити поле. |
|
|
~ |
~ |
|
F = qE |
|
|
Знаючи вектор напруженостi електричного поля, знаходимо силу, що дорiвню¹ добутку вектора напруженостi електричного поля i будь-якого заряду.
Остання формула визнача¹ силу дi¨ на певний заряд (не qïðîá).
2
1.4 Напруженiсть електричного поля. |
1 Електродинамiка |
1.4.1Напруженiсть електричного поля точкового заряду (рис 1.06)
~ |
|
qqïð |
~r |
|||
Fê = |
|
4 0r2 r |
||||
~ |
~ |
|
|
q |
|
|
Fê |
|
|
~r |
|||
E = |
qïð |
= |
|
4 0r2 r |
||
~er = |
~r |
|
|
|||
|
r - орт радiус вектора |
|||||
~ |
|
q~er |
|
|
|
|
E = |
4 "0r2 |
|
|
|||
1.4.2Принцип суперпозицi¨ для електричного поля
Для електричних полiв викону¹ться принцип суперпозицi¨, за яким напруженiсть електричного поля в т. простору дорiвню¹ сумарнiй напруженостi всiх напруженостей полiв в цiй точцi
Беремо 2 поля i точку |
~ |
~ ~ |
~ |
|
~ |
E~ = Pi |
E~i. |
||
|
|
|
E1, |
E2. E = E1 |
+ E2 |
|
|
||
У цiй точцi заряд q |
|
|
|
|
|
|
|
||
~ ~ |
~ |
~ |
~ |
~ |
~ |
|
~ |
|
|
F = qE = q(E1 |
+ E2) = qE1 + qE2 |
= F1 |
+ F2 |
|
|
||||
Принцип суперпозицi¨ призводить до незалежностi дi¨ сил з боку кожного з полiв
Напруженiсть всерединi атомiв |
10 |
11 |
10 |
17 |
 . На поверхнi важкого ядра |
E |
~ |
10 |
22 Â |
|
|
|
ì |
|
ì |
Незважаючи на це, дослiди показують, що принципи суперпозицi¨ виконуються з високою точнiстю, але можлива поляризацiя вакуму.
1.4.3Електричне поле системи точкових зарядiв (рис 1.7)
~ P ~ E = Ei
i
~1 q1(~r ~r1) E1 = 4 "0 j~r ~r1j3
~1 q1(~r ~ri) Ei = 4 "0 j~r ~rij3
~ |
|
|
|
1 qi(~r ~ri) |
|
|
||||
E = Pi |
|
|
|
|
|
|
||||
4 "0 j~r ~rij3 |
q (x x ) |
|||||||||
|
x |
Pi |
4 "0 ((x xi)2 |
+(y yi)2+(z zi)2) 2 |
||||||
E = |
|
|
1 |
|
|
|
|
i |
i |
|
|
|
|
|
|
|
|
|
3 |
||
1.4.4Напруженiсть електричного поля неперервно розподiлених зарядiв
1.4.4.1Об'¹мний розподiл Для характеристики розподiлу неперервних зарядiв вводять поняття густини розподiлених
зарядiв
= |
q |
, V ! 0. |
V |
q ! V; = dVdq
Âiäïîâiäíî dq = dV (ðèñ 1.8)
Нам вiдома об'¹мна густина |
||||||||||
Треба розрахувати ~ |
|
|||||||||
|
|
|
|
|
|
|
|
E в т. А, положення яко¨ зада¹ться радiус-вектором ~r |
||
Розiб'¹мо на малi дiлянки dV . |
||||||||||
dq = (~r)dV , |
dq - точковий |
|||||||||
dE~ = |
1 |
|
|
dq |
|
|
~r ~r0 |
|
||
4 "0 j~r ~r0j |
2 |
|||||||||
|
|
|
j~r ~r0j |
|||||||
|
|
1 |
|
|
(~r0)(~r ~r0)dV |
(для об'¹мно розподiленного заряду) |
||||
E = 4 "0 V |
||||||||||
|
j~r ~r0j3 |
|||||||||
3
1.5 Сила вза¹модi¨ мiж зарядженими тiлами |
1 Електродинамiка |
1.4.4.2Поверхневий розподiл У провiдникiв заряди розподiляються по поверхнi.
По поверхнi задають поверхневою густиною зарядiв
= q ; S ! 0
S
q ! S; = dSdq
dq = dS
Розглянемо довiльне тiло (рис 1.09 (в розробцi) )
dE~ = |
|
1 |
|
|
dq |
|
|
~r ~r0 |
|
|
4 "0 j~r ~r0j |
2 |
|||||||||
|
|
j~r ~r0j |
||||||||
~ |
|
1 |
|
S |
(~r)(~r ~r0)ds |
|||||
E(~r) = |
|
4 "0 |
|
|
j~r ~r0j3 |
|
||||
1.4.4.3Лiнiйний розподiл У випадку лiнiйного розподiлу заряду
|
q |
dq |
= |
l , l ! 0, = dl , |
|
dq = dl
Беремо заряджену нитку (рис 1.10)
~ |
|
|
|
|
|
|
|
|
|
|
Eв т. А характеризу¹ ~r |
||||||||||
dq = (~r0)dl |
|
|
|
|
||||||
dE~ = |
1 |
|
|
|
dq |
|
|
~r ~r0 |
||
4 "0 j~r ~r0j |
2 |
|
||||||||
|
|
j~r ~r0j |
||||||||
|
|
1 |
|
|
|
0)(~r ~r0)dl |
||||
E~ (~r) = |
l |
(~rj~r ~r0j3 |
||||||||
4 "0 |
||||||||||
[ ] = Êë
ì3
[ ] = Êë
ì2
[ ] = êë
ì
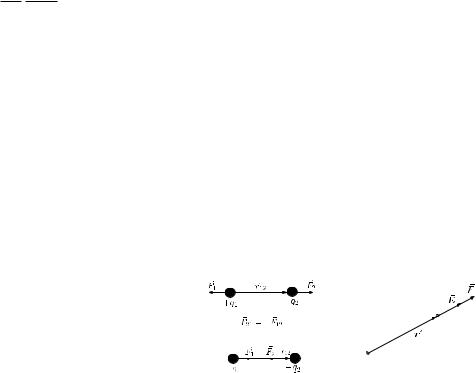
1.5Сила вза¹модi¨ мiж зарядженими тiлами
Розглянемо 2 тiла об'¹мна густина котрих 1 i 2 (ðèñ 1.11)
~
F = E1dq2
розраху¹мо силу. з якою 1 дi¹ на 2 dq1, dq2 - точковi, тодi
dF~ = |
1 |
|
dq |
1 |
dq |
(~r00 ~r0) |
|
|
|||
4 "0 |
|
|
|||||||||
|
|
|
|
|
2 j~r00 ~r0j3 |
|
|
||||
|
1 |
|
|
|
|
|
0 |
00)(~r00 |
~r0)dV |
dV |
|
F~ = |
V1 V2 |
|
1(~r |
) 2(~rj~r00 ~r0j3 |
1 2 |
||||||
4 "0 |
|
|
|
|
|||||||
або у випадку поверхневого розподiлу заряду другого тiла
|
1 |
|
0 |
|
|
00)(~r00 ~r0)dV |
dS |
|
F~ = |
V1 S2 |
1(~r |
) 2(~rj~r00 ~r0j3 |
1 2 |
|
|||
4 "0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2
1
1.11 |
1.12 |
1.13 |
4