
MDVM
.pdf1
“Методи дослідження властивостей матеріалів”
1.Розшифровка рентгенограм полікристалічного зразка металу кубічної сингонії.
2.Як проводиться ідентифікація фаз за даними про міжплощинні відстані?
3.Основний закон послаблення монохроматичного рентгенівського випромінювання.
4.Прецизійне вимірювання періодів кристалічної гратки.
5.Зйомка в камері КРОС.
6.Вивести рівняння Вульфа-Бреггів та вказати на практичні аспекти застосування.
7.Якісний фазовий рентгеноструктурний аналіз сплавів.
8.Методи кількісного фазового рентгеноструктурного аналізу (Метод «гомологічних» пар, метод внутрішнього стандарту).
9.Виникнення характеристичного рентгенівського спектру.
10.Основне рівняння дифракції рентгенівських променів. Рівняння Лауе.
11.Індиціювання дебаєграм полікристалів кубічної сингонії.
12.Асиметричний метод зйомки дебаєграм та їхній розрахунок. Метод Лауе.
13.Прецизійне визначення періоду кристалічної гратки за допомогою дифрактометра.
14.Метод Речінгера.
15.Прецизійне визначення періодів гратки. Метод екстраполяції.
16.Метод полікристалів.
17.Аналіз методу за допомогою оберненої гратки.
1)Розшифровка рентгенограм полікристалічного зразка металу кубічної
сингонії.
Електронограми від полікристалів. Електронограми з суцільними дифракційними максимумами найбільш придатні для структурних досліджень. З їх допомогою можна проводити фазовий якісний і кількісний аналізи, визначати параметри кристалічної гратки, встановлювати тип кристалічної гратки і розміщення атомів у ній. Електронограми можна з успіхом використовувати для досліджень субструктури, динаміки кристалічної гратки тощо.
Електронограми від полікристалу найбільш зручні для мікрофотометричних вимірювань інтенсивностей дифракційних максимумів. У них майже відсутні ефекти
двомірної дифракції і багатократного відбиття. Для полікристалічного зразка не існує “мертвої зони” і це дає змогу повною мірою використовувати правила погасання для визначення типу кристалічної гратки. Дифракційні максимуми від полікристалічного зразка чіткі, що сприяє більш точному визначенню параметрів кристалічної гратки. Однак інформація, яку можна одержати із дифракційної картини полікристалічного зразка, є цінною лише в тому випадку, коли відомі кристалографічні індекси дифракційних максимумів.
Для знаходження кристалографiчних iндексiв hkl використовують квадратичну форму для кубiчних кристалiв
1 |
|
h2 k 2 l 2 |
(45) |
|
d 2 |
a 2 |
|||
|
|
i основне рiвняння електронографiї rd = Lλ (46)
Тут d-мiжплощинна вiдстань; a-постiйна кристалiчної гратки; Lλ - постiйна приладу; r-радiус дифракцiйного кiльця. Пiдставивши (5) в (45), одержимо

2
|
r 2 |
|
|
h2 k 2 l 2 |
|
, |
|
|
(L )2 |
|
|
a 2 |
|||
|
|
|
|
|
|||
звiдки |
|
|
|
|
|
|
|
|
r 2 ( |
L |
)h2 k 2 l 2 |
A(h2 k 2 l 2 ) (19) |
|||
|
|
||||||
|
|
|
a |
|
|
|
|
Формула (46) дає змогу, вимiрявши радiуси дифракцiйних кiлець, проiндексувати електронограму. Iндексування електронограм полегшується тим, що кубiчнi кристали дають мало дифракцiйних максимумiв, i їх розмiщення вiдповiдає певним закономiрностям, якi випливають iз правил погасання для кубiчних кристалiв.
Справдi, iнтенсивнiсть дифракцiйного максимуму пропорцiйна квадрату структурної амплiтуди, яку в загальному виглядi можна записати
F fi e2 i(hx ky lz) (47)
i
де fi - атомний фактор розсiяння; x, y, z - координати атомiв.
Iз формули (47) видно, що для примiтивної кубiчної гратки з координатами атома 000 структурна амплiтуда не дорiвнюватиме нулевi при всiх значеннях
кристалографiчних iндексiв; для об'ємоцентрованої кубiчної гратки (координати 000,
12 , 12 , 12 ) структурна амплiтуда вiдмiнна тодi вiд нуля, коли сума кристалографiчних
iндексiв дорiвнює парному числу. У гранецентрованiй гратцi координати атомiв 000, 12 , 12 ,0 , 12 ,0, 12 , 0, 12 , 12
i структурна амплiтуда не дорiвнюватиме нулевi за умови, що всi iндекси парнi або непарнi. Аналогiчнi правила погасання можна встановити i для iнших кубiчних граток, наприклад для гратки типу алмазу, типу NaСl тощо. Цi закономiрностi дають змогу, аналiзуючи вiдношення квадратiв радiусiв дифракцiйних максимумiв, визначити тип кристалiчної гратки
2)Як проводиться ідентифікація фаз за даними про міжплощинні відстані?
Кожна фаза володіє своєю кристалічно-ю структурою, характерезується пев-ним притаманим тільки даній фазі на-бором дискретних значень міжплощи-них відстаней d/n від максимального і нижче. Як випливає з р-ня Вульфа-Бре-га, кожному значенню міжплощин-ної відстані відповідає лінія на ренгеногра-мі від полікристалічного зразка під пев-ним кутом θ (λ=const). Таким чином пе-вному набору міжплощиних відстаней для кожної фази на ренгенограмі буде відповідати певна система ліній (диф-ракційних максимумів). Відносна інте-нсивність цих ліній на ренгенограмі залежить перш завсе від структури фа-зи. Звідци, визначивши місце розташу-вання ліній на ренгенограмі (кут θ) і знаючи довжину хвилі випромінюван-ня, на якому була знята ренгенограма, можна визначити значення міжплощин-их відстаней d/n за формулою Вульфа-Брега: d/n= λ/2sin
θ.
Визначивши набір d/n досліджуваного матеріалу і спідставевши з раніше відо-мими данними d/n для чистих речовин їх різних сполучень, можно встановити яку фазу складає матеріал. Слід підкре-слити що визначається саме фаза, а не хімічний склад, але останій іноді мо-жна вивести якщо існують додаткові данні про елементний склад той чи ін-шої фази. Данні про міжплощинні відстані для різних фаз можна знайти в спеці-альних таблицях, довідковій літературі та в журнальних статтях.
3)Основний закон послаблення монохроматичного рентгенівського
випромінювання.
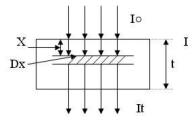
Виведемо формулу , що описує закон послаблення рентгенівських променів при проходженні певної речовини , товщиною t .
3
Загальний закон , який кількісно визна-чає послаблення будь-яких однорідних променів в речовині , яка ці промені поглинає , можна сформулювати так :
В рівних товщинах однієї і тієї ж одно-рідної речовини поглинаються рівні до-лі енергії одного і того ж випромінення
dI/I = - μ d x (5.1)
На монохромати-чне рентгенівське випромінення (λ) , інтенсивністю І○ , після проходження пластинки товщиною t , інтенсивність дорівнює Іt . В середині палстинки , на глибині х виділено тонкий шар , товщи-ною dx . В цьому шарі послаблення рентгенівських променів можна описа-ти формулою (5.1) . Знак “-” вказує на те , що інтенсивність рентгенівських променів , що пройшли пластинку dx зменшується . Щоб знайти залежність інтенсивності від товщини всієї пласти-нки t , проінтегруємо
формулу (5.1) : |
|
|
|
Іt |
t |
|
|
∫dI/I=∫-dx (5.2) |
|||
I○ |
0 |
|
|
|
It |
t |
|
|
Ln | = - μ x | |
(5.3) |
|
|
I○ |
0 |
|
|
LnIt/I○=- t (5.4) |
||
|
It =I○ e- t |
(5.5) |
|
Основний закон послаблення рентгені-вських променів . Коефіцієнт - ліній-ний |
|||
коефіцієнт послаблення |
рентге-нівських променів , його розмір м-1. Якщо t=1(1 м ) , |
||
то тоді =-lnI1/I○ |
(5.6) |
|
|
Тобто , -характеризує відносне змен-шення інтенсивності рентгенівських променів на шляхув 1м . Лінійний кое-фіцієнт послаблення залежить від при-роди поглинаючої речовини (z) , до-вжини хвилі ( ) , від температури та агрегатного стану
4) Прецизійне вимірювання періодів кристалічної гратки.
Період кристалічної гратки дуже важлива характеристика для металів і сплавів. Вимірюючи точно ці параметри можливо:
1.визначити концентрацію розчинного елемента в твердому розчині.
2.Визначити структурний тип твердих розчинів.
3.Виміряти пружні напруги в матеріалі і визначити їх знак.
4.Співставляючи періоди кристалічної гратки при різних температурах можна визначити коефіцієнт термічного розширення різних фаз.
4.Аналізуючи зміну а (період кристалічної гратки) пересиченого твердого розчину при його розпаді можна встановити закономірності кінетики процесу, яких суттєво змінює властивості сплавів. Для кристалів кубічної сингонії період гратки визначають за формулами:

4
|
|
|
|
|
|
|
a |
|
H 2 |
K 2 L2 |
(16.1) |
||
|
|
|||||
2Sin |
||||||
|
|
|
|
|
||
|
|
2d Sin n |
|
|||
Для того, щоб провести прецезійний розрахунок а, необхідно дуже точно виміряти кут θ, розрахувати d/n, проіндиціювати рентгенограму і визначити зв’язок між d/n, HKL і а, розрахувати період гратки а. Формула для відносної похибки визначення міжплощинної відстані:
d |
|
|
(25.1) |
|
|||
|
ctg |
||
d |
|
|
|
Щоб зменшити d/d, необхідно, щоб кут θ був максимальним. Прецезійний інтервал кута θ = 60 – 84 ˚. Також необхідно, щоб Δθ було мінімальним, тобто вимірюють кут за допомогою спеціальної техніки.
n 2d sin
0 2 dsin 2d cos
продиференцюємо по d і θ:
(26.1)
dsin d cos |
(26.2) |
|
d |
ctg |
(26.3) |
d |
|
|
Із (26.3) витікає, що при одній і тієї ж похибці визначення кута θ-(Δθ), Δd/d прямує до
нуля при θ, що прямує до 90˚. Для кубічної гратки d a .
d a
Джерела похибок у визначенні періодів кристалічної гратки.Існує три види похи-бок, що призводять до неточності визна-чення міжплощинних відстаней:
1.Випадкові похибки, пов’язані з визначенням положення рентгенівської лінії на рентгенограмі (дифрактограмі).
2.Систематичні похибки, зумовлені геометрією зйомки.
3.Похибки, зумовлені фізичними факторами.
При фотографічному методі реєстрації дифракційної картини вимірюють положення середини рентгенівської лінії. Для більш точного розрахунку необхідно визначити центр ваги рентгенівської лінії. Похибка виміру залежить від ширини рентгенівської лінії, Чим ширша лінія, тим менша похибка. Якщо вимір здійснюється лінійкою, похибка складає 0,2 мм. Якщо використовують оптичні прилади – компаратори, то похибка складає 0,01 мм. Вимірювання потрібно проводити багаторазово (бажано кількома дослідниками) і результати потім усереднювати. Для дуже точних розрахунків необхідно використовувати мікрофотометри, які дозволяють визначити розподіл густини почорніння вздовд рентгенограми.
|
I0 |
|
|
(26.4) |
lg I |
|
|||
|
|
|||
– густина почорніння |
I |
- інтенси-вність падаючого світла |
||
|
|
|
|
0 |
І – інтенсивність світла, що пройшло скрізь плівку
За допомогою мікрофотометричних кривих необхідно знайти центр ваги максимумів, що відповідають рентгенівським лініям, а потім з великою точністю знаходять відстань між ними (2l). Продиференцюємо (R – стала):

5
l (26.5)
2R
Можна підвищити точність визначення кута θ, якщо проводити зйомку в рентге-нівських камерах з більшим радіусом .Але збільшувати радіус камери не вигідно, ос-кільки зростає експозиція а також похиб-ка, пов’язана з розходимістю первинного пучка рентгенівських променів.
При використанні дифрактометрів положення дифракційної лінії може бути визначено із значно більшою точністю, ніж при фотометоді. Для збільшення точності необхідно працювати в дискретному (кроковому) режимі з великою тривалістю експозиції і малою величиною кроків. Для отриманих профілей необхідно розраховувати центр ваги.
Систематичні похибки при зйомці зразків на дифрактометрі.
1. Відхилення поверхні зразка від фокусуючої поверхні. Призводить до похибки у визначенні міжплощинної відстані
d cos2 d
2. Зміщення поверхні зразка від осі гоніометра. В цьому випадку теж
d cos2 d
3. Проникнення рентгенівських променів вглиб зразка
d cos2 d
4. Неточна установка нульового положення лічильника
d ctg d
5. Вертикальна розходимість первин-ного променя
d cos2 d
5) Зйомка в камері КРОС.
Схема камери КРОС.
1.станина (основа)
2.передня стійка (нерухома)
3.касета з плівкою (рухома)
4.тримач зразка (закріплюється у задню стінку , яка може рухатися)
5.зразок
6.задня стійка
7.мотор

6
№лінії |
|
2l |
L |
|
2 |
tg(180 2 ) |
a ,нм |
0 |
|
a |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Де a точність вимірювання періоду решітки, l Atg (180 2 ) - умова фокусування, А – відстань між плівкою та зразком, l – половина відстані між симетричними дифракційними
лініями, знаходимо умову фокусування |
x Atg 2 (2 ) , |
х – відстань між щілиною та |
||||||||||||
плівкою, тоді період кристалічної решітки дорівнює: |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a |
|
|
|
h2 k 2 l 2 ; |
|
|||||||||
|
|
|
|
|
|
|||||||||
2sin |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
a M |
1 |
|
|
a M ( |
cos |
) ; |
||||||||
sin |
sin 2 |
|||||||||||||
|
|
|
|
|
|
|||||||||
l Asec2 |
(180 2 ) |
; |
|
|||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|||||
тоді: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|||||||
|
. |
|
||||||||||||
2Asec2 (180 2 ) |
|
|||||||||||||
6) Вивести рівняння Вульфа-Бреггів та вказати на практичні аспекти застосування.
Формула Вульфа-Бреггів виводиться при неточних передумовах:
1)будемо вважати, що рентгенівські промені дзеркально відбиваються від атомних площин
2)будемо вважати, що атоми нерухомі
3)будемо вважати, що заломлення відсутнє
Нехай на кристал падають паралельні монохроматичні рентгенівські промені з довжиною хвилі λ під кутом ковзання Θ. В рентгенографії кут ковзання ( Θ )-це кут між падаючим променем і атомною площиною.
Наше завдання з’ясувати у яких випадках “ відбиті ”промені в результаті інтерференції дадуть максимум, тобто в цьому випадку вони будуть відбиватися від кристалу і ми можемо їх зареєструвати за допомогою рентгенівської плівки або лічильника.
Оптична різниця ходу (ОРХ ) = nλ ( 2.1)-умова максимуму
Нам необхідно знайти оптичну різницю ходу когерентних променів 1 і 2, і тоді умовою максимуму буде рівняння ( 2.1 ), де n=1, 2, 3…
7
Виразимо ОРХ через міжплощинну відстань d і кут Θ.
ОРХ=АВ-АС ( 2.2 )
Знайдемо АВ з АВС |
|
|
|
|
|||
sin |
АК |
|
АВ |
АК |
|
d |
|
АВ |
sin |
sin |
|||||
|
|
|
|||||
(2.3)
Знайдемо АС з АВС
АС=АВ·cos2Θ ( 2.4 )
ОРХ АВ АС |
d |
|
d |
cos 2 |
d |
1 1 2 sin 2 |
|
d |
2 sin 2 2d sin n |
|
sin |
sin |
sin |
sin |
|||||||
|
|
|
|
|
|
|||||
2d·sinΘ = nλ |
( 2.5 ) - рівняння Вульфа-Бреггів |
|
|
|
||||||
Число n називається |
порядком відбиття, фізичний зміст |
цієї величинице кількість |
||||||||
довжин хвиль, які вкладаються в ОРХ.
Виконання рівняння ( 2.5 ) є умовою ”відбиття” променів від даної атомної площини
(площин ). Ця формула виконується з великою точністю незважаючи на те, що вона була виведена при невірних передумовах.
Використовуючи цю формулу ми можемо: якщо відома довжина хвилі
випромінення, то вимірюючи кут Θ, можемо знайти d/n і таким чином з’ясувати природу досліджуваної речовини її структуру та багато інших питань.В цьому суть
рентгено-структурного аналізу. Якщо відома міжплощинна відстань кристалу то вимірюючи Θ можемо розрахувати λ і з’ясувати хімічний склад досліджуваного матеріалу. В цьому суть рентгено-спектрального аналізу.
7) Якісний фазовий рентгеноструктурний аналіз сплавів. |
|
|
|
|
Кожна фаза, сполука має свій набір міжплощинних відстаней |
d |
і значення |
d |
|
n |
n |
|||
|
|
розраховується по рентгенограмам чи дифрактограмам, звідти ми визначаемо і значення інтенсивності ліній.
Порівнюючи ці данні з таблицями, визначаємо фазовий склад аналізуючої речовини, що аналізуються.
Порівнювання починається з найбільш інтенсивних ліній.
Якщо 3-4 інтенсивних ліній, фази яку ми передбачаємо не спостерігається, то цієї фази в зразку немає. Для детального пошуку фазового складу треба скористатися міжнародною картотекою кристалографічних даних ASTM в яку входять всі кристалографічні данні, які друкуються в наукових роботах.
8
8) Методи кількісного фазового рентгеноструктурного аналізу (Метод «гомологічних» пар, метод внутрішнього стандарту).
Оснований на тому, що інтенсивність ліній даної фази пропорційна об’ємній долі даної фази в суміші. Тобто кількісний фазовий аналіз оснований на кількісному порівняні інтенсивності ліній різних фаз одна з одною або з інтенсивністю ліній еталона. Тому для кількісного фазового аналізу в основному треба використовувати дифрактометри. Зйомки необхідно проводити в кроковому режимі. Він більш точний, ніж неперервний.
Для більшої точності, необхідно проводити режими з великим часом експозиції і малим кроком. Порівняння інтенсивності здійснюється на “аналітичних” лініях – це лінії з максимальною інтенсивністю, які не співпадають з іншими. Тому перед проведенням кількісного аналізу треба проводити якісний аналіз.Проаналізуємо деякі методи:
1. Метод підмішування внутрішнього стандарту.
Він застосовується тільки для порошкоподібних зразків.
До порошку який аналізується, підмішують відому кількість порошку еталона (стандарту), ретельно перемішують і проводять зйомку. Потім з’ясовується відношення інтенсивності
аналітичних ліній фази і стандарту, що аналізується I ст I ф .
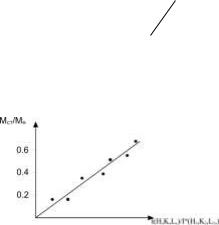
Попередньо будують графік для двохфазної суміші – фази і стандарту, в таких координатах:
Рис. 39
I |
СТ |
|
M |
СТ |
|
|
f |
|
|
|
|
|
|
|
|
||
IФ |
|
M |
Ф |
||
|
|
|
|||
де Мст і Мф – маси стандартної речовини і фази.
По цьому графіку знаходять відношення об’ємних долей, потім знаючи кількість стандартної речовини, яку ми домішували до зразка, визначаючи кількість фази, яка нас цікавить.
Таким методом було встановлено вміст шпінелі (FeO3 Cr2O3) в вогнетривкому матеріалі.
Недолік цього методу в тому, що додавання еталонної речовини приводить до розбавлення фаз, які визначаються , а це знижує чутливість і точність аналізу кількості фази (якщо її кількість мала).
2. Метод гомологічних пар.
В цьому методі порівнюють інтенсивність ліній двох фаз. Попередньо складають таблицю гомологічних пар.
9
В цьому методі з’ясовують, яка пара сусідніх ліній двох різних фаз має однакову інтенсивність. Потім по таблиці з’ясовують % кількість фази, яку ми досліджуємо. Таким чином можна визначити співвідношення кількості аустеніту і мартенситу в загартованій сталі.
9) Виникнення характеристичного рентгенівського спектру.
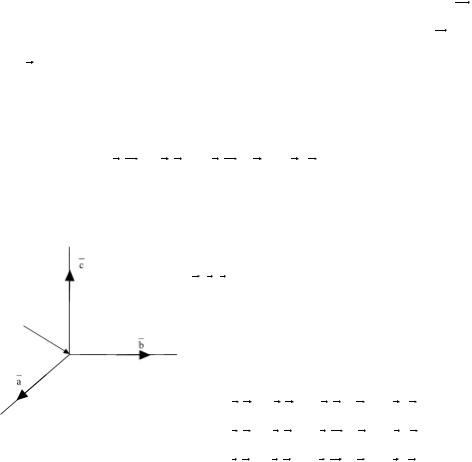
Виникнення характеристичного спектру може бути пояснено таким чином:
Електрон, що рухається з великою швидкістю “влітає” в атом і вибиває з внутрішньої орбіти електрон. Атом у такому стані буде збуджений і буде мати підвищену енергію. Такий стан атома не стійкий і він переходить у нормальний стан в результаті того, що електрон з більш високої орбіти переходить на вакантне місце. Такий перехід супроводжується зменшенням енергії атома, і ця енергія виділяється у вигляді кванту рентгенівського випромінювання.
Енергія цього кванту дорівнює:
hv E1 E2 ,
де E1 , E2 енергії електрону, коли він рухається по початковій, далекій і кінцевій близькій орбітах.
Якщо електрон, вибитий з К-орбіти то в результаті таких переходів буде виникати К- серія характеристичного спектру.
Якщо електрон переходить з L-рівня на К- буде виникати K - лінія спектру.
Якщо з М рівня на К – виникає K - лінія.
Так як існують підрівні, то виникає тонка структура спектру K 1 і K 2 , K 1 і K 2
лінії. Перехід з М – рівня на К-рівень електрона має меншу вірогідність ніж перехід з L – рівня на К, оскільки М-рівень знаходиться на більшій відстані від К. Тому інтенсивністьліній у 5 разів менша ніж ліній.
Якщо електрон вибитий з L – рівня, то в результаті переходу електронів з більш високих рівнів виникає L – серія і т.д.
Оскільки відстань між К і М рівнем більша, ніж К і L, то довжина хвилі лінії більша ніж лінії.ї
10
10) Основне рівняння дифракції рентгенівських променів. Рівняння Лауе
 При рентгенографічному дослідженні аналізують інтерференційні картини, які утворюються в результаті розсіювання рентгенівських променів електронами атомів.
При рентгенографічному дослідженні аналізують інтерференційні картини, які утворюються в результаті розсіювання рентгенівських променів електронами атомів.
Розглянемо інтерференцію рентгенівських променів атомами, які розташовані у вигляді ланцюга.
Введемо спрощуючі передумови.
1.Будемо вважати, що атоми нерухомі.
2.Всі електрони атома зосереджені в узлі гратки.
Нехай на атоми, які розташовані ланцюгом , падає плоска хвиля монохроматичного випромінювання під кутом косинус якого дорівнюе . Розсіяні промені розходяться під кутом косинус якого дорівнює .
Одиничний вектор в напрямку падаючих променів позначимо S0 , а одиничний вектор в напрямку розсіювання цих променів позначимо через S .
a вектор, це період розташування атомів вздовж ланцюга.
Умовою того, що розсіяні промені 1 і 2 в результаті інтерференції дадуть максимум є те, |
|
||||||||||
що оптична різниця ходу цих променів буде дорівнювати цілій кількості довжин хвиль, |
|
|
|||||||||
тобто Н , (Н- ціле число). Оптична різниця ходу променів 1 і 2 буде: |
|
|
|
|
|
|
|
||||
PX AB CD a S a S 0 a S S 0 a S H a a 0 a 0 |
|
(8.1) |
|
|
|
|
|||||
Рівняння (8.1) є умовою того, що розсіяні рентгенівські промені і результаті |
|
|
|
|
|||||||
інтерференції дадуть максимум. Це і е перше рівняння Лаує |
|
|
|
|
|
|
|
||||
При проходженні рентгенівських променів через |
|
|
|
|
|||||||
просторову гратку з осями вздовж яких періоди складають |
|
|
|||||||||
a,b, c, а косинус кутів між падаючим променем і осями |
|
|
|
|
|||||||
складають 0 , 0 , 0 , а косинус кутів між розсіяним променем |
|||||||||||
і осями , , , то по аналогії з одновимірним випадком |
|
|
|
||||||||
умовою максимуму в результаті інтерференції буде |
|
|
|
|
|||||||
виконання 3X одночасно рівнянь (8.1, 8.2, 8.3): |
|
|
|
|
|
|
|
||||
a S a S 0 a S S 0 a S H a a |
0 |
a 0 |
(8.1) |
||||||||
|
b S 0 |
|
b S S 0 |
b S K b b 0 |
|
|
|
|
|
||
|
b 0 |
|
|
||||||||
b S |
|
(8.2) |
|||||||||
c S |
c S 0 |
|
c S S 0 |
c S L c c |
0 |
c |
0 |
|
(8.3) |
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
або скорочено:
a 0 |
H ; |
8.1 |
|
b 0 |
K ; |
8.2 |
Ці рівняння називаються рівняннями Лаує. |
c 0 L ; |
8.3 |
|
|
Їх можна записати в векторній формі:
