
Text_lektsiy_z_TTD_chastina_1__3-y_sem_ukr_2015
.pdf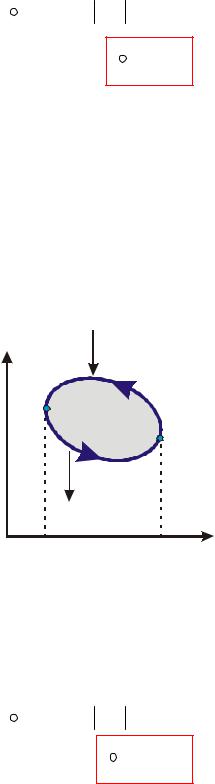
Розділ 1: Лекція № 4 |
31 |
процесу 2б1 ( dv < 0 , lподв = l2б1 < 0 - РТ стискується)
Сума робіт в циклі
∫δl =l1а2 − l2б1 = lцикла > 0 (площа 1а2б1)
∫δl ≠ 0
Упрямих циклах lцикла є продукцією циклу (цей цикл призначений для отримання роботи), тому lцикла часто називається корисна робота циклу.
2)Зворотні цикли
Реалізуються в холодильних установках (ХУ), теплонасосних установках (ТНУ)..
Зображується в плоских координатах проти ходу годинникової стрілки
|
lпідв=l2б1 <0 |
|
p |
б |
|
1 |
lцикла <0 |
|
|
|
|
|
2 |
|
|
a |
|
|
lвідв=l1а2 >0 |
|
v1 |
v2 |
v |
Зворотний цикл складається з двох процесів: процес 1а2 ( dv > 0 , lотв = l1а2 > 0 - РТ розширюється)
и
процес 2б1 ( dv < 0 , lподв = l2б1 < 0 - РТ стискується) Сума робіт в циклі
∫δl =l1а2 − l2б1 = lцикла < 0 (площа 1а2б1)
∫δl ≠ 0
Особливість зворотних циклів – оскільки lцикла < 0 , на реалізацію зворотного циклу необхідно витратити роботу (підводити із зовнішнього середовища).
ТТД (3-й семестр) |
2015 р. |

Розділ 1: Лекція № 4 |
32 |
1.7.2ТЕПЛОТА ПРОЦЕСУ
Кількість теплоти в рівноважному процесі дорівнює
2
q1− 2 = ∫Tds
1
Відповідно до цього виразу кількість теплоти можна представити графічно
в Ts координатах у вигляді площі, що обмежена кривою рівноважного процесу і віссю s .
T |
|
1 |
|
|
|
б |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Рівноважний процес: |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
δq = Tds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
T - тепловий потенціал (причи- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
на); |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
δq |
|
|
s - узагальнена координата. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
s |
2 |
s |
||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
ds
З діаграми видно, що кількість теплоти залежить від характеру процесу, подібно до того, як це наголошувалося для роботи процесу.
Аналіз рівняння :
1.) Теплота рівноважного процесу в Ts координатах еквівалентна площі під кривою процесу. При цьому теплота q1a 2 буде менше ніж теплота q1б2 ( q1a 2 < q1б2 )
2)Якщо ds > 0 (ентропія в процесі зростає), то q > 0 . - теплота підводиться до
РТ.
Якщо ds < 0 (ентропія в процесі зменшується), то q < 0 . - теплота відводить-
ся від РТ
Якщо ds = 0 s = const (изоентропний процес), то q = 0 (немає теплообміну, процес адіабатний).
3)Прямі цикли.
УTs координатах (діаграмі) прямі цикли зображуються за годинниковою стрілкою.
ТТД (3-й семестр) |
2015 р. |
Розділ 1: Лекція № 4 |
33 |
qпідв=q1а2 >0
T |
a |
|
|
|
1 |
б 2
2
|
qвідв=q2б1 <0 |
|
|
s |
s |
2 |
s |
1 |
|
||
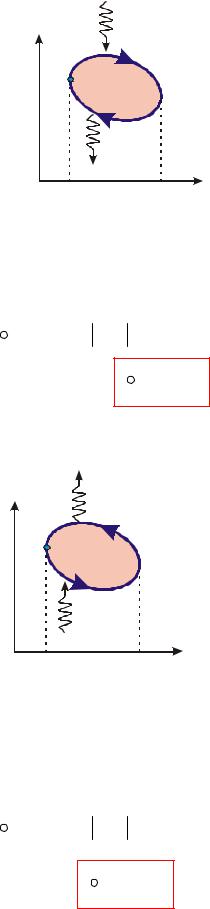
Прямий цикл складається з двох процесів: |
|||
процесу 1а2 ( ds > 0 , qподв = q1а2 > 0 - тепло підводиться до РТ) та
процесу 2б1 ( ds < 0 , qотв = q2б1 < 0 - тепло відводиться від РТ) Сума теплот за цикл
∫δq =q1а2 − q2 б1 = qцикла > 0 (площа 1а2б1)
∫δq ≠ 0
4)Зворотні цикли
Зворотний цикл зображується в плоских координатах проти годинникової
стрілки.
qвідв=q2б1 <0
Tб
1
a 2
2
|
qпідв=q1а2 >0 |
|
|
s |
s |
2 |
s |
1 |
|
||
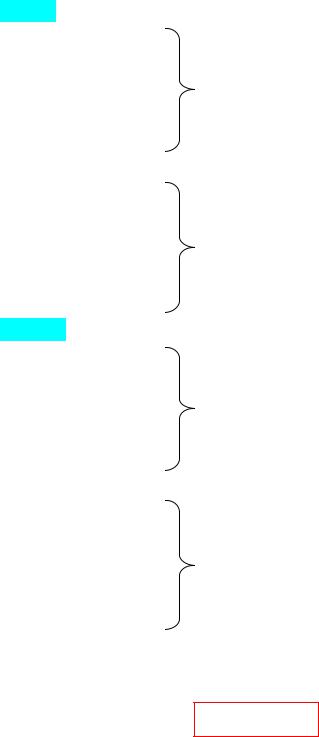
Зворотний цикл складається з двох процесів:
процесу 1а2 ( ds > 0 , qподв = q1а2 > 0 - тепло підводиться до РТ) та
процесу 2б1 ( ds < 0 , qотв = q2б1 < 0 - тепло відводиться від РТ) Сума теплот в циклі
∫δq =q1а2 − q2 б1 = qцикла < 0 (площа 1а2б1)
∫δq ≠ 0
ТТД (3-й семестр) |
2015 р. |
Розділ 1: Лекція № 4 |
34 |
Питання для самоперевірки знань з ТТД за Розділом 1 (лекції №4)
1.Рівняння для визначення роботи та теплоти в рівноважних процесах (в повних та питомих величинах:
Робота -
δL = pdV
2Деформаційна робота для рівно-
L = ∫ pdV |
важних процесів в повних вели- |
1чинах.
2
L = ∫δL
1
δl = pdv
2Деформаційна робота для рівно-
l = ∫ pdv |
важних процесів в питомих ве- |
1личинах.
2
l = ∫δl
1
Теплота -
δQ = TdS
2
Q = ∫TdS
1
2
Q = ∫δQ
1
δq = Tds
2
q = ∫Tds
1
2
q = ∫δq
1
Вираз для теплоти в рівноваж- них процесах (у повних величи-
нах).
Вираз для теплоти в рівноважних процесах (у питомих величинах).
2.Узагальнений вираз для різних видів енергетичних взаємодій в рівноважних процесах. Дати пояснення до членів рівняння.
δE = y dX
δE - елементарна кількість енергії, що передається у формі відповідного виду роботи;
y - узагальнена сила (потенціал), величина, що породжує дану взаємодію (причи-
на);
X - узагальнена координата даної взаємодії (заряд) - величина, яка змінюється за наявності даної взаємодії (ознака того, що взаємодія має місце).
3. Фізичний зміст ентропії:
ТТД (3-й семестр) |
2015 р. |
Розділ 1: Лекція № 4 |
35 |
ентропія є мірою хаотичності руху мікрочасток, з яких складається тіло.
При підводі до системи (тіла) енергії у формі теплоти, міра хаотичності руху
мікрочасток зростає (зростає внутрішня невпорядкованість, хаотичність), а
при відведенні - навпаки, зменшується.
4.Графічне представлення результатів енергообміну (робота в pv координа-
тах):
в pv координатах площа під кривою процесу 1-2 ( обмежена кривою рівно-
важного процесу і віссю абсцис) є деформаційною роботою процесу
p |
1 |
|
б |
|
|
|
|
||
|
|
|
a |
|
|
|
|
2 |
|
|
|
p |
δl |
|
|
|
|
|
|
|
v1 |
|
v2 |
v |
|
|
|
dv |
|
Рівноважний процес:
δl = pdv
2
l = ∫ pdv
1
p- причина (потенціал);
v - узагальнена координата.
Якщо dv > 0 , то l > 0 . - газ розширюється, робота відводиться (здійснюється газом).
Якщо dv < 0 , то l < 0 . - газ стискується, робота підводиться (витрачається на стискування).
Якщо dv = 0 v = const ( процес ізохорний), то l = 0
5.Графічне представлення результатів енергообміну (теплота в Ts координатах)
кількість теплоти можна представити графічно в Ts координатах у вигляді пло- щі, що обмежена кривою рівноважного процесу і віссю s
T |
|
1 |
|
б |
|
|
|
|||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
Рівноважний процес: |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
δq = Tds |
||||||
|
|
|
|
|
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
q = ∫Tds |
|
|
T |
|
|
|
|
|
δq |
||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
T - причина (тепловий потенціал); |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s - тепловий потенціал. |
|
|
s |
|
|
|
|
|
|
|
s |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
s |
||||
|
1 |
|
|
|
|
|
|
|
|
|
||||
ds
Якщо ds > 0 (ентропія в процесі зростає), то q > 0 . - теплота підводиться до РТ.
Якщо ds < 0 (ентропія в процесі зменшується), то q < 0 . - теплота відводить-
ся від РТ
ТТД (3-й семестр) |
2015 р. |

Розділ 1: Лекція № 4 |
36 |
Якщо ds = 0 s = const (изоентропний процес), то q = 0 (не має теплообміну, процес адіабатний).
6.Від чого залежить величина роботи (теплоти) процесу 1-2 Робота (теплота) є функцією процесу, тобто залежить від шляху (характеру)
процесу 1-2 і визначається площею під кривою процесу (робота - в pv координатах, теплота - в Ts координатах)
7.Де реалізуються прямі цикли, як зображуються в pv та Ts координатах: Прямі цикли - реалізуються в теплових двигунах (ДВС, ГТУ, ПТУ .) де теп-
лота перетворюється на роботу. Теплоту отримують, використовуючи первинні енергоресурси нафта, вугілля, газ, мазут і так далі. У координатах (діаграмі) прямі цикли зображуються по ходу годинникової стрілки.
p |
lвідв=l1а2 >0 |
|
|
qпідв=q1а2 >0 |
|
|||
a |
|
|
|
T |
|
a |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
lцикла >0 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
б |
|
|
|
б |
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
lпідв=l2б1 <0 |
|
|
|
qвідв=q2б1 <0 |
|
||
|
|
|
|
|
|
|
||
v |
v |
2 |
|
v |
s1 |
|
s2 |
s |
1 |
|
|
|
|
|
|
|
|
Що таке робота прямого циклу: сума робіт в циклі
∫δl =l1а2 − l2б1 = lцикла > 0 (площа 1а2б1)
∫δl ≠ 0
Упрямих циклах lцикла є продукцією циклу (цей цикл призначений для виробництва роботи), тому lцикла часто називається корисна робота циклу.
Що таке теплота прямого циклу: Сума теплот за цикл
∫δq =q1а2 − q2 б1 = qцикла > 0 (площа 1а2б1)
∫δq ≠ 0
8. Де реалізуються зворотні цикли, як зображуються в pv Ts координатах: Зворотні цикли реалізуються в холодильних установках (ХУ), теплонасосних установках (ТНУ). Зображуються в плоских координатах проти ходу годинникової стрілки
ТТД (3-й семестр) |
2015 р. |

|
|
Розділ 1: Лекція № 4 |
|
|
37 |
|
lпідв=l2б1 <0 |
|
qвідв=q2б1 <0 |
|
|
p |
б |
T |
|
б |
|
1 |
|
|
|
||
1 |
|
|
|
|
|
lцикла <0 |
|
|
|
|
|
|
|
a |
2 |
|
|
|
2 |
|
|
|
|
|
a |
|
|
|
|
|
lвідв=l1а2 >0 |
|
qпідв=q1а2 >0 |
|
|
|
s1 |
|
s2 |
s |
|
v1 |
v2 |
|
|||
v |
|
|
|
||
Що таке робота зворотного циклу:
сума робіт в циклі ∫δl =l1а2 − l2б1 = lцикла < 0 (площа 1а2б1)
∫δl ≠ 0
Особливість зворотних циклів – оскільки lцикла < 0 , на реалізацію зворотного циклу необхідно витратити роботу (підводити із зовнішнього середовища).
Що таке теплота зворотного циклу:
сума теплот в циклі∫δq =q1а2 − q2 б1 = qцикла < 0 (площа 1а2б1)
а)
б)
в)
г)
∫δq ≠ 0
9.Навести рівняння ізобарного, ізохорного, ізотермічного та ізоентропного рівноважних процесів та рівняння для визначення термодинамічної роботи, через початкові та кінцеві параметри відповідних процесів :
2
p = const (ізобарний процес) l = ∫ pdv = p ( v2 − v1 )
1
2
v = const (ізохорний процес) l = ∫ pdv = 0 , так как dv = 0 ( v 2 = v1 )
1
|
|
2 |
|
v2 |
|
|
|
|
p2 |
|
|
|
pv = const ( ізотермічний процес T = const ) l = ∫ pdv = p1v1 |
ln |
= −RT ln |
|
|
||||||||
v1 |
p1 |
|
||||||||||
|
|
1 |
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
k −1 |
|
|
|
|
p1v1 |
|
|
k |
|||||||
|
k |
|
|
|
|
|||||||
pv |
|
= const (ізоентропний процесс s = const ) l = ∫ pdv = |
|
1 |
− |
p2 |
|
|||||
|
|
1 |
k − 1 |
|
p1 |
|
|
|||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ТТД (3-й семестр) |
2015 р. |

Розділ 1 |
Лекція №5 |
38 |
Лекція № 5 |
|
Дата:_________ |
1.8 РІВНЯННЯ ДЛЯ ВИЗНАЧЕННЯ КІЛЬКОСТІ ТЕПЛОТИ І РОБОТИ В ПРОЦЕСАХ З ТЕРТЯМ
Процеси з тертям - умовно-рівноважні і нерівноважні (обидва нерів-
новажні).
ТЕПЛОТА ПРОЦЕСУ
Q* - загальний тепловий ефект процесу:
|
|
Q* = Q + Q |
r |
|
|
|
|
|
|
тут Q |
- зовнішній теплообмін ( >, <, = 0); |
|||
Qr |
- теплота тертя ( ≥ 0 ) (внутрішній теплообмін) завжди підводить- |
|||
ся до тіла, тому свій знак не міняє. |
|
|
||
Q та Qr - |
на стан робочого тіла впливають однаково, як на хаотичну форму |
|||
руху. |
|
|
|
|
Теплота тертя Qr впливає на зміну стану РТ подібно до додаткового зовніш-
нього теплопідводу в кількості Qr > 0 .
Ентропія реагує на хаотичний рух, тобто на загальний тепловий ефект процесу. Враховуючи це, можна записати:
2
Q + Qr = ∫Tds
1
δQ + δQr = Tds |
Вирази для теплоти в процесах з |
|
|
2 |
тертям в повних величинах |
Q + Qr = ∫(δQ + δQr ) |
|
|
|
1 |
|
Якщо врахувати, що |
Q = q m , Qr |
= qr m та S = s m , тоді : |
|
2 |
|
q + qr = ∫Tds |
|
|
|
1 |
|
δq + δqr |
= Tds |
Вирази для теплоти в процесах з |
|
2 |
тертям в питомих величинах. |
q + qr = ∫(δq + δqr ) |
|
|
|
1 |
|
ТТД (3-й семестр) |
2015р. |

Розділ 1 |
Лекція №5 |
39 |
ГРАФІЧНА ИНТЕРПРИТАЦИЯ РІВНЯННЯ |
|
|
T |
1 |
|
Умовно |
|
T |
1 |
Нерівноважний |
|
|
|
|
|
|||||
|
|
|
рівноважний |
|
|
|
процес |
|
|
|
|
процес |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
q+q |
|
|
|
q+qr |
|
|
|
|
r |
|
|
|
|
|
|
s |
1 |
s |
s |
|
s1 |
s2 |
s |
|
|
2 |
|
|
|
|
Переконаємося, що процеси з тертям необоротні. Розглянемо два процеси:
1-2 –( прямий процес)
q зовнішній підвід тепла ( >0)
2-1 - зворотний процес
q зовнішній відвід тепла ( <0)
|
|
|
|
|
|
|
qr>0 |
|
|
q |
* |
qr>0 |
|
|
q* |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q2 −1 + qr 2 |
1 |
|
|
|
|
2 |
|
|
−1 = ∫Tds |
|||
|
|
|
|
|
|
|
|
||
|
|
q1− 2 + qr 1− 2 = ∫Tds |
|
|
|
|
2 |
||
|
|
|
1 |
|
|
|
|
|
|
|
|
Права частина рівняння - площа під кривою процесу |
|||||||
|
|
2 |
|
або q1*− 2 = |
|
q2* −1 |
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
||||
|
|
∫Tds = |
∫Tds |
|
|
|
|||
|
|
1 |
|
2 |
|
|
|
|
|
|
|
qr 1− 2 = qr 2 −1 |
- теплота тертя свій знак не міняє |
|
|||||
q1− 2 < q2 −1
Кількість теплоти, що підводиться в прямому процесі 1-2, буде менше ніж кількість теплоти, що відводиться в зворотному процесі 2-1 при проходженні робочого тіла через ті ж стани. Це означає, що джерело теплоти при
обернені процесу не повернеться у вихідний стан. Це означає, що дані проце-
си є необоротними.
ДЕФОРМАЦІЙНА РОБОТА.
f - поверхность поршня
Q
L
При розширенні РТ, частина роботи розши-
2
рення ( ∫ pdV )витрачатиметься на подолання
1
тертя ( Lr ).У зовнішнє середовище через по-
dx |
верхню поршня передаватиметься робота |
|
2 |
||
|
контрольная поверхность |
L = ∫ pdV − Lr |
системы |
1 |
ТТД (3-й семестр) |
2015р. |

Розділ 1 |
Лекція №5 |
40 |
Робота тертя Lr |
завжди витрачається, що враховується в цьому рівнянні зна- |
|
ком «-». Lr свій знак в цьому рівнянні міняти не буде, тобто Lr |
> 0 (завжди |
|
!). Це означає:
якщо в розрахунках із застосуванням цього рівняння отримано Lr < 0 , то висновок один - такий процес неможливий.
Для узагальнення цього виразу на випадок стиснення, досить прийняти,
2
що величини ∫ pdV та L - алгебраїчні,
1
2
L = ∫ pdV − Lr
1
δ L = pdV − δ Lr
2 2
L = ∫δL; Lr = ∫δLr ;
1 1
2
тобто ∫ pdV < > 0 , L < > 0 .
1
Вирази для деформаційної роботи в процесах з тертям в повних величинах
Якщо врахувати, що L = l m ,
2
l = ∫ pdv − lr
1
δ l = pdv − δ lr
2 2
l = ∫δl; lr = ∫δlr ;
Lr = lr m та V = v m , тоді :
Вирази для деформаційної роботи в процесах з тертям в питомих величинах.
1 1
ГРАФІЧНА ІНТЕРПРЕТАЦІЯ РІВНЯННЯ
p |
1 |
|
Умовно |
|
p |
1 |
Нерівноважний |
|
||
|
|
|
|
|||||||
|
|
|
рівноважний |
|
|
процес |
|
|||
|
|
|
процесс |
|
|
|
|
|
||
|
|
|
2 |
|
|
|
2 |
|
||
|
|
|
l+lr |
|
|
|
l+lr |
|
||
|
v |
1 |
|
v |
v |
|
v1 |
v |
v |
|
|
|
|
|
|
|
|
|
|
|
|
Розглянемо два процеси: |
|
|
|
|
||||||
|
1-2 – прямий процес |
|
2-1 - зворотний процес |
|||||||
|
|
|
2 |
|
|
|
1 |
|
||
|
l1− 2 + lr 1− 2 = ∫ pdv |
|
|
l2 −1 + lr 2 −1 = ∫ pdv |
||||||
|
|
|
1 |
|
|
|
2 |
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
∫ pdv = |
∫ pdv |
|
lr 1− 2 = lr 2 −1 |
- робота тертя свій знак не міняє, тоді |
|||||
|
1 |
|
|
2 |
|
|
|
|
|
|
l1− 2 < l2 −1
ТТД (3-й семестр) |
2015р. |
