Text_lektsiy_z_TTD_chastina_1__3-y_sem_ukr_2015

2. КРУГОВІ І НЕКРУГОВІ ПРОЦЕСИ.

а) Кругові процеси або цикли - сукупність процесів, при здійснення яких

РТ повертається у вихідний стан. Таким чином, цикл - круговий процес робочого тіла.

кою ) працюють теплові двигуни, за зворотними циклами (проти годинникової стріл-

кои) - холодильні установки (ХУ), тепло-насосні установки (ТНУ).

б) Некругові або розімкнені процеси - початковий і кінцевий стани не спів-

падають. Цикли можна розбити на декілька розімкнених процесів.

3 . ОБОРОТНІ І НЕОБОРОТНІ ПРОЦЕСИ.

Ця класифікація враховує не лише характер зміни стану РТ, але і особливо-

сті його енергообміну із зовнішніми джерелами (із зовнішнім середовищем), з

якими РТ утворює ізольовану систему.

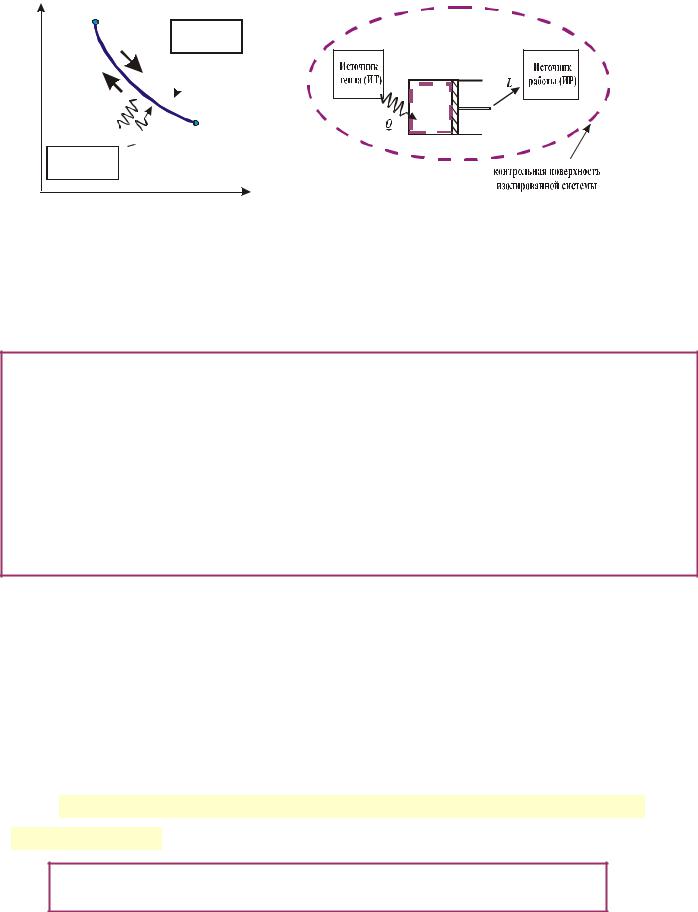
а) Оборотний процес - процес (уявний), що гранично ідеалізується, допус-

кає можливість його протікання в протилежному напрямку через ті ж стани РТ і

до того ж так, що всі складові ізольованої системи, здійснюючи прямий і зворот-

ний процес, повертається у вихідний стан (само тіло і джерела). (Не плутати обо-

ротний і зворотний процес).

L

2

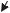
Q

Источник

теплоты

v (T)

Пізнавальна цінність оборотних процесів: вони мають найвищу енергетич-

ну ефективність і тому є еталоном енергетичної ефективності для реальних про-

цесів.

УМОВИ ОБОРОТНОСТІ ТЕПЛОМЕХАНІЧНИХ ПРОЦЕСІВ

1) Відсутність тертя в РТ ( δLr = δQr = 0 ) –рівноважний процес (гідравлічний опір дорівнює 0 ) - умова внутрішньої оборотності

2) Теплообмін між РТ і джерелом теплоти повинен протікати при нескінченно малій різниці температур Tр.т . − Tд.т . = dT >< 0 ( практично Tр.т. = Tи.т. ) - умова зов-

нішньої оборотності

З розгляду двох умов оборотності витікає, що кожен оборотний процес

обов'язково рівноважний ( Lr = Qr = 0 ), але не кожен рівноважний є оборотним

зважаючи ( завдяки) на другу умову оборотності (вона може не виконуватися).

Друга умова оборотності виконується в адіабатних процесах, в яких робо-

че тіло не віддає і не отримує теплоту із зовні.

За визначенням адіабатний процес – це процес, що протікає без зовніш-

нього теплообміну.

Ознака адіабатного процесу: δQ = 0 Q = 0

Отже: адіабатний оборотний процес = адіабатний рівноважний.

Введемо поняття узагальненого тертя (механічне, термічне, електричне,

магнітне, хімічне ). Узагальнене тертя породжує узагальнений опір, де і протікає процес переходу впорядкованого руху в хаотичний. Тоді оборотний процес - це процес, що протікає без узагальненого тертя і відповідно без узагальненого опо-

ру. Тобто, в ньому немає переходу впорядкованого руху в хаотичний.

б) Необоротний процес - це процес, в якому хоч би одна з умов оборотнос-

ті не виконується. Тоді процеси умовно рівноважні і нерівноважні (протікають з тертям) - завідомо необоротні.

Всі реальні процеси - необоротні.

У пропонованому курсі ми вивчатимемо дві необоротності реальних проце-

сів:

·пов'язані з тертям

·пов'язані з теплообміном при кінцевій різниці температур між РТ і

джерелом.

Завдання інженера: необхідно навчитися розрізняти ці необоротності і зна-

ти технічні рішення, за допомогою яких їх можна зменшувати.

Питання для самоперевірки знань з ТТД за Розділом 1 (лекція №3).

1.Термодинамічний процес – будь яка послідовна зміна стану робочого тіла (системи) під впливом енергообміну із зовнішнім середовищем.

2.Рівноважний процес - це безперервна послідовність рівноважних станів РТ, можливий при нескінченно повільному протіканні процесу і відсутності тертя. Таким чином, це процес, що ідеалізується.

Lr = Qr > 0 ), але для яких з достатньою для практики точністю всі проміжні стани і кінцеві можна вважати рівноважними.

5.Нерівноважні процеси - реальні процеси, що характеризуються неоднаковістю параметрів по всій масі РТ в проміжних станах (В курсі ТТД вивчають такі нерівноважні процеси, в яких проміжні стани,

- не рівноважні, а початковий і кінцевий - обов'язково рівноважні.)

6.Кругові процеси або цикли - сукупність процесів, в результаті здійснення, яких РТ повертається у вихідний стан.

7.Цикл - круговий процес робочого тіла.

8.По прямим циклам (за годинниковою стрілкою ) працюють теплові двигуни, за

зворотними циклами (проти годинникової стрілки) - холодильні установки (ХУ), тепло-насосні установки (ТНУ).

9.Оборотний процес - процес (уявний), що гранично ідеалізується, допускає можливість його протікання в протилежному напрямку через ті ж стани РТ і до того ж так, що всі складові ізольованої системи, здійснюючи прямий і зворотний процес, повертається у вихідний стан (само тіло і джерела). (Не плутати оборотний і зворотний процес).

10.Пізнавальна цінність оборотних процесів: вони мають найвищу енергети-

чну ефективність і тому є еталоном енергетичної ефективності для реальних процесів

11.Умови оборотності тепломеханічних процесів

1) Відсутність тертя в РТ ( δLr = δQr = 0 ) –рівноважний процес (гідравлічний опір дорівнює 0 )

2) Теплообмін між РТ і джерелом теплоти повинен протікати при нескінченно малій різниці температур Tр.т. − Tи.т. = dT ( практично Tр.т. = Tи.т. )

Яка умова оборотності завідомо виконується в адіабатних процесах – друга, бо за визначенням адіабатний процес протікає без зовнішнього теплообміну.

12.Необоротний процес - це процес, в якому хоч би одна з умов оборотності

не виконується.

Дві необоротності реальних процесів: 1) тертя по ходу РТ

2) теплообмін при кінцевій різниці температур T ( t ) між РТ і джере-

лом.

1.6ТЕПЛОМЕХАНІЧНА ВЗАЄМОДІЯ В РІВНОВАЖНИХ ПРОЦЕСАХ. ВИЗНАЧЕННЯ

КІЛЬКОСТІ ТЕПЛОТИ І РОБОТИ В РІВНОВАЖНИХ ПРОЦЕСАХ ДЛЯ ЗАКРИТИХ СИСТЕМ.

Мірою механічної і теплової взаємодії є відповідно кількість теплоти і ро- боти. При кількісній оцінці енергообміну розрізняють роботу і теплоту

а) у рівноважних процесах (ознака Lr = Qr = 0 ) б) у реальних процесах (ознака Lr = Qr > 0 )

Для технічних цілей важливо отримати Q і L через параметри робочого тіла (системи).

1.6.1. ДЕФОРМАЦІЙНА (ТЕРМОДИНАМІЧНА) РОБОТА В РІВНОВАЖНИХ ПРОЦЕСАХ.

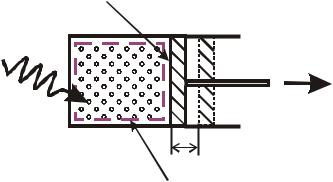
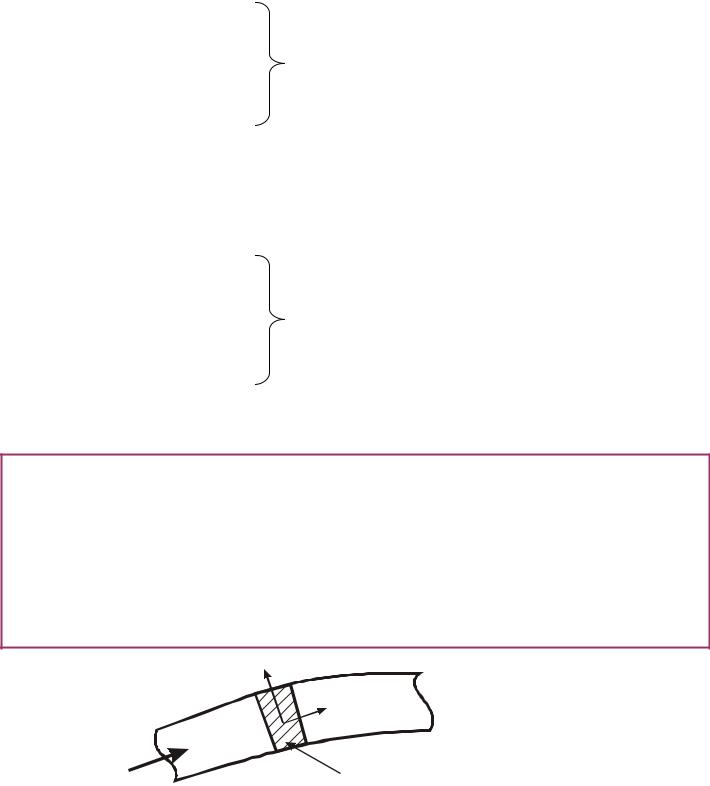
Розглянемо закриту систему. Газ в циліндрі може стискуватися і розширю- ватися, при цьому обмінюючись енергією із зовнішнім середовищем через повер-

хню поршня у формі роботи розширення або стискання. Якщо РТ розширюєть-

ся, то РТ долає опір зовнішнього середовища і виконує роботу; при стискуванні зовнішнє середовище виконує роботу над газом.

f - площа поршня

Робота=сила × путь

δL = p f dx = p dV

Елемен- сила Путь тарна робота

Величина δL є енергією, яка передається у формі роботи через контрольну

поверхню закритої системи. При стискуванні ( dV < 0 ) маємо δL < 0 , ( робоче тіло отримує роботу). При розширенні (δV > 0 ) маємо δL > 0 (робоче тіло віддає енер-

гію у формі роботи).

1важних процесів в повних вели-

З урахуванням того, що L = l m и V = v m

δl = pdv

1важних процесів в питомих ве-

Примітки:

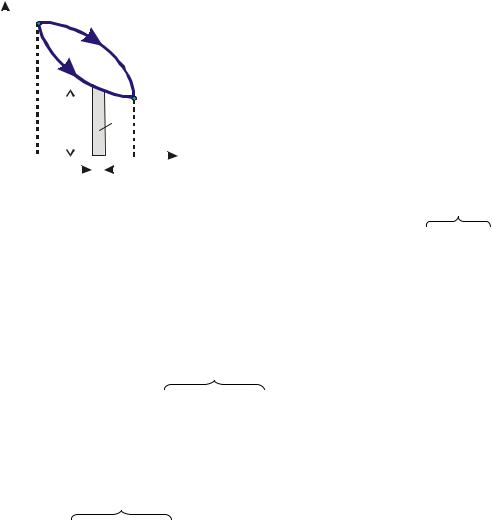
а) Отримані вирази справедливі для будь-якої конфігурації виділеного об'єму РТ за умови, що система розглядається як закрита система.

б) Отримані вирази справедливі для будь-якої закритої системи ( m = const ): тобто не лише для не потокових процесів, але і для потокових процесів, в яких виділений об'єм розглядається, як закрита система.

y

x

Звернемо увагу, що зміна об'єму є ознакою того, що енергообмін у формі дефор-

маційної роботи має місце. Причиною, що породжує цей енергообмін, є тиск.

1.6.2. УЗАГАЛЬНЕНІ ВИРАЗИ ДЛЯ РІЗНИХ ВИДІВ ЕНЕРГЕТИЧНИХ ВЗАЄМОДІЙ (У ФОРМІ ВІДПОВІДНОГО ВИГДУ РОБОТИ) В РІВНОВАЖНИХ ПРОЦЕСАХ.

З курсу фізики відомо, що в рівноважних процесах при енергетичних взає-

модіях елементарна кількість енергії, що передається може бути представлена в узагальненому вигляді

δE = y dX

δE - елементарна кількість енергії, що передається у формі відповідного виду ро-

боти;

y - узагальнена сила (потенціал), величина, що породжує дану взаємодію (причи-

на його);

X - узагальнена координата даної взаємодії (заряд) - величина, яка змінюється за наявності даної взаємодії (ознака того, що взаємодія має місце).

У виразу для деформаційної роботи роль потенціалу (причина) виконує аб-

солютний p тиск, а роль координати взаємодії - об'єм V .

1.6.3. ЕЛЕМЕНТАРНА КІЛЬКІСТЬ ТЕПЛОТИ В РІВНОВАЖНИХ ПРОЦЕСАХ

Аналогічно δE = y dX для елементарної кількості теплоти можна записати де δQ - елементарна кількістьδ Q =енергіїTdS , що передається у формі теплоти;

T - термодинамічна температура [K], узагальнена сила (тепловий потенціал), причина, що породжує дану взаємодію у формі теплоти;

S - ентропія - величина, зміна якої є ознакою теплової взаємодії (узагальнена координата).

Факт існування ентропії і її зміни під впливом теплової взаємодії безпосере-

дньо виявити неможливо, оскільки він не пов'язаний ні з одним фізичним ефектом,

який дозволяє спостереження або вимір. У цьому полягає складність сприйняття ентропії. На відміну від ентропії всі інші величини, що входять в узагальнене рів-

няння δE = y dX можна виміряти.

Правомірність існування ентропії встановлюється зіставленням всіх виснов-

ків, які виходять з рівняння δQ = T dS , з даними значного досвіду, накопиченого

людством. Безумовний експериментальний і науковий факт існування ентропії

вводиться в науку як принцип існування ентропії і відноситься до другого закону

термодинаміки.

Фізичний сенс ентропії розкривається в статистичній фізиці, яка вивчає мікроскопічну структуру речовини із залученням теорії вірогідності. Там показа-

но, що ентропія є мірою хаотичності руху мікрочасток, з яких складається ті-

ло. При підводі до системи (тілу) енергії у формі теплоти, міра хаотичності руху

мікрочасток зростає (зростає внутрішня невпорядкованість, хаотичність), а при ві-

дведенні - навпаки, зменшується.

У рівноважних процесах, відповідно до рівняння δQ = T dS знак теплоти, як алгебраїчної величини, залежить від характеру зміни ентропії тіла:

якщо теплота підводиться до тіла (δQ > 0 ),то ентропія (міра хаотичності) збільшується ( dS > 0 ),а при відведенні (δQ > 0 ) – зменшується ( dS < 0 ).

δQ = TdS

1них процесах (у повних величи-

З урахуванням того, що Q = q m та S = s m

δq = Tds

Зауваження по розділу 1.6:

1.Формули для Q, L ( l , q ) виведені для закритих систем і можуть застосовуватися для не потокових (типу циліндра з поршнем) і потокових процесів.

2.Отримані формули справедливі не лише для рівноважних процесів, але і для оборотних, бо друга умова оборотності не впливає на виведення отриманих

формул.

1.У отриманих виразах величини теплоти і роботи – алгебраїчні , тобто можуть мати знак «+» та «-».

. З цього місця матеріал наданий для студентів як СРС до Лекції №4

1.7ГРАФІЧНЕ ПРЕДСТАВЛЕННЯ РЕЗУЛЬТАТІВ ЕНЕРГООБМІНУ (ДЕФОРМАЦІЙНОЇ

РОБОТИ І КІЛЬКОСТІ ТЕПЛОТИ) В РІВНОВАЖНИХ І ОБОРОТНИХ ПРОЦЕСАХ.

1.7.1. ДЕФОРМАЦІЙНА РОБОТА

2

Кількість роботи в рівноважному процесі дорівнює l1− 2 = ∫ pdv

1

Для вирішення інтеграла необхідно знати залежність p = p(v ) у процесі, тобто рівняння процесу. З рівняння для деформаційної роботи, витікає, що в pv ко-

ординатах площа під кривою процесу 1-2 ( обмежена кривою рівноважного про- цесу і віссю абсцис) є деформаційною роботою процесу.

Оскільки площа під кривою процесу (рівноважного і оборотного) еквівалентна роботі, то діаграму часто називають робочою.

Ааналіз:

1) Робота є функцією процесу, тобто залежить від шляху процесу 1-2 і визначається площею під кривою процесу. При цьому робота l1a 2 буде менше ніж робота

l1б2

l1a 2 < l1б2

2)Якщо dv > 0 , то l > 0 . - газ розширюється, робота відводиться (здійснюється газом).

Якщо dv < 0 , то l < 0 . - газ стискується, робота підводиться (витрачається на стискування).

Якщо dv = 0 v = const ( процес ізохорний), то l = 0 .

3)Прямі цикли - реалізуються в теплових двигунах (ДВС, ГТУ, ПТУ .) де теп-

лота перетворюється на роботу. Теплоту отримують, використовуючи первинні енергоресурси (ПЕР): нафта, вугілля, газ, мазут і так далі. У pv координатах (діаграмі) прямі цикли зображуються по ходу годинникової стрілки.

Прямий цикл складається з двох процесів:

процесу 1а2 ( dv > 0 , lотв = l1а2 > 0 - РТ розширюється)

та