
konspect_lectsiy-ln_lm
.pdf
|
Ln,xn |
Gк,Y п |
І |
L x |
І |
|
|
G Y |
dF |
|
|
|
|
Gп, Y к |
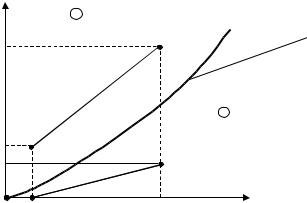
Рис. 17.6. Схема протитечійного масообмінного апарату.
До апарату надходить рідка фаза з масовими витратами Ln і концентрацією цільового компонента хn. Витрати рідкої фази на виході з апарату позначимо Lk і концентрацією цільового компонента в рідкій фазі – хк.
Протитечією з низу колони подається газова фаза з витратами Gn: концентрацією цільового компонента yn. На виході з апарату витрати газової фази позначимо через Gk і концентрацію цільового компонента – yк.
Проведемо довільно в апараті перетин І-І і позначимо витрати рідкої фази L і концентрацію х витрати, газової фази G і концентрацію у.
Запишемо рівняння матеріального балансу за матеріальними потоками для цього ж перерізу і низу колони :
L + Gn = G + LК ,
а також рівняння по розподіленому компоненту :
LX +СnYn = GY + LkХk
Розв’язуючи рівняння відносно У, отримаємо рівняння робочої лінії:
Y L X GYn LX k G G
Робоча лінія характеризує залежність між робочими концентраціями розподіленої речовини в фазах.
Якщо концентрації фаз мало змінюються по висоті, то можна прийняти:
Gn=G, LK=L
|
|
Y |
L |
X |
|
GYn LX k |
|
L |
X Y |
|
L |
X |
|
(17.12) |
|||
|
|
|
|
|
|
|
|
|
k |
||||||||
|
|
|
G |
|
G |
|
|
G |
n |
|
G |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
Позначивши |
L |
A, B |
GYn |
LX k |
|
, отримаємо вираз робочої лінії в вигляді: |
|
||||||||||
G |
|
G |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Y= АX + В
Тобто, робоча лінія процесу масопередачі - це пряма з тангенсом кута нахилу: lg = A GL
З другого боку, рівняння робочої лінії можна отримати і інакше. Виділимо елемент поверхні в апараті dF, концентрація цільового компонента в фазах L і G змінюються на dx і dy. Запишемо кількість маси, яка переходить із фази G, в границях цього елементу, до фази L( знак "-" говорить про зменшення концентрації.)
dM=G(-dY)=L*dX -GdY = Ldx |
(17.13) |
Проінтегруємо це рівняння в межах від початкової до кінцевої концентрації, покладаючи, що G та L апараті постійні (носії).
Yk |
Xk |
|
|
|
|
|
|
|
|
|
|
||||||
M G( dY ) Ldx |
|
|
|
|
|
|
|
|
|
|
|||||||
Yn |
Xn |
|
|
|
|
|
|
|
|
|
|
||||||
|
G(Yn Yk ) L( Xk |
|
Xn ) |
(17.14) |
|||||||||||||
З цього рівняння матеріального балансу можна знайти питомі витрати поглинача: |
|||||||||||||||||
|
|
|
|
|
|
L |
Yn Yk |
|
|
|
|
|
|||||
|
l |
|
|
|
|
|
|
|
|
|
|||||||
|
G |
X k X n |
|
|
|
||||||||||||
Рівняння (17.13) і (17.14) запис рівняння матеріального балансу масообмінних процесів в |
|||||||||||||||||
диференційній та інтегральній формах. |
|
|
|
|
|
|
|
|
|
|
|||||||
Інтегруючи рівняння (17.13) від низу колони до перетину І-І, одержимо: |
|||||||||||||||||
|
G( Yn Y ) L( X k X ), |
|
|||||||||||||||
|
Y |
L |
X Y |
L |
|
|
|
|
|
(17.15) |
|||||||
|
|
X |
|
|
|
||||||||||||
|
|
|
|
|
k |
|
|||||||||||
|
|
G |
|
n |
G |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Рівняння (17.12) і (17.15) є ідентичними. |
|
|
|
|
|
|
|
|
|
||||||||
Для випадку прямотоку рівняння має вигляд: |
|
|
GYn |
|
|||||||||||||
|
|
|
L |
|
|
LX n |
|
|
|||||||||
|
Y |
|
X |
|
|
|
|
|
|
|
|
||||||
|
G |
|
|
|
G |
|
|
|
|||||||||
Робочу лінію можна побудувати по точкам Yn та Хк і Хn |
та Yк, координати яких |
||||||||||||||||
характеризують верх і низ апарата. |
|
|
|
|
|
|
|
|
|
|
|||||||
Графічне зображення процесу. Напрямок процесу переносу
Графічний процес масообміну можна представити у вигляді робочої лінії AB, яка будується по заданим робочим концентраціям, і кривою рівноваги, яка будується або за формулою, або за дослідними даними. Робоча лінія розташовується вище лінії рівноваги, або нижче, що визначається напрямком переносу речовини з фази G до фази L (розглянутий випадок), або з фази L в фазу G, коли робоча лінія розташована нижче кривої рівноваги рис. 17.7.
Y
M |
|
|
|
|
G L |
B |
Y |
P |
= f(x) |
|
||||
|
|
|
||
Yn |
|
|
|
|
|
|
M |
|
|
A |
L L |
|
|
|
B' |
|
|
|
|
Yк |
|
|
|
|
|
|
|
|
|
A' |
|
|
|
|
Yп=0 |
Хк (X'п) |
|
|
|
Хn (X'к) |
X |
|
|
|
Рис. 17.7. Графічна інтерпретація робочої лінії процесу.
Механізм процесу масопередачі
Механізм переносу маси в процесі масопередачі зводиться до двох видів переносу - переносу речовини за рахунок молекулярної дифузії і переносу речовини за рахунок вихрової дифузії, яка інакше називається турбулентною дифузією.
Перший випадок має місце в нерухомому середовищі та при ламінарному його русі, а другий - в рухомому, коли речовина в основному переноситься частинами середовища і перенос його визначається гідродинамічними обставинами, тобто турбулентністю потоку. При цьому молекулярна дифузія також має місце. Сукупний перенос речовини за рахунок молекулярної і вихрової дифузії отримав назву конвективної дифузії. Таким чином, механізм масопередачі зводиться до молекулярної і конвективної дифузії.
Молекулярна дифузія. Перший закон Фіка
При молекулярній дифузії перенос речовини здійснюється молекулами, які знаходяться в хаотичному русі і повільно переміщуються в газі, переносячи тим самим енергію і масу. Рух молекул не зв'язаний з рухом потоків газу і рідини.
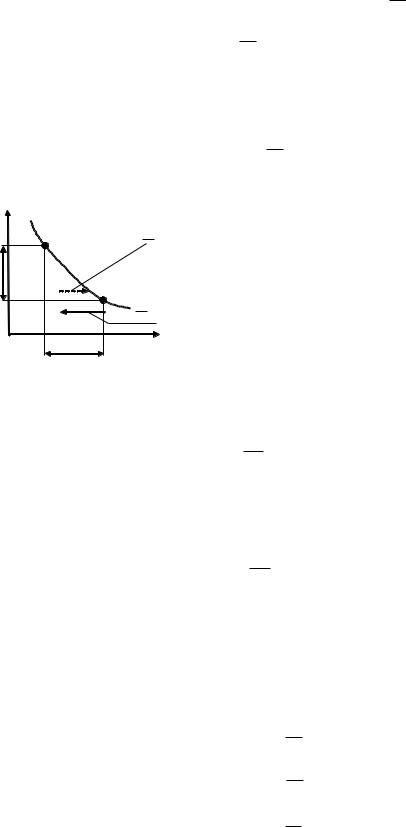
Перший закон Фіка визначає кінетику процесу переносу.
Кількість речовини dМ, яка дифундує за час dτ через елементарну площину dF, розташовану перпендикулярно напрямку дифузії, пропорційна градієнту концентрації dcdx :
dM D dcdx dFd
Знак мінус ("-") вказує на те, що концентрація речовини зменшується. Коефіцієнт пропорційності D - називається коефіцієнтом дифузії.
Якщо віднести масу компоненту, що продифундував, до одиниці площі і одиниці часу, то отримаємо вираз для дифузійного потоку J. І перший закон Фіка можна записати:
J qm D dcdx
Компонент дифундує в напрямку зменшення мольної частки цільового компонента. Тобто напрямок дифузійного потоку J та градієнта концентрації протилежні.
C |
|
|
j D dc |
|
dx |
C |
|
|
dc |
|
dx |
x |
X |
Рис. 17.8 Напрямок дифузійного потоку і градієнту концентрації при молекулярній дифузії.
Аналіз першого закону Фіка показує, що він аналогічний, з одного боку - закону в'язкості Ньютона, якому підпорядковуються всі ньютонівські рідини:
dwdx ,
де τ - дотична напруга, |
dv |
- градієнт швидкості і – коефіцієнт пропорційності, коефіцієнт |
|
dx |
|||
|
|
в'язкості.
А з іншого боку - одномірному формулюванню закону теплопровідності Фурьє: qm dTdx
Коли температура залежить тільки від однієї координати х. Тут |
dT |
- градієнт температури, |
|
dx |
|||
|
|
— коефіцієнт теплопровідності.
Перший закон Фіка можна також записати в векторній формі:
qM = - D c
Якщо вважати, що перенос маси проходить в ізотропному середовищі і коефіцієнт дифузії D
має одне і теж значення для всіх трьох напрямків, по яких змінюється концентрація, запишемо: qx D cx
qy D yc qz D cz
А це різні проекції одного й того ж векторного співвідношення, записаного вище. qm=-DgradC
Якщо в'язкість і теплопровідність є фізичними константами, залежними тільки від
температури, тиску, то і коефіцієнт дифузії D також є фізичною константою, але ця величина для бінарної системи залежить від температури, тиску і концентрації .
Коефіцієнт дифузії має розмірність :
D |
Mdx |
|
|
кгм |
|
|
|
м2 |
або |
м2 |
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
с |
|||||||
|
dcF |
|
|
кг / м |
год |
|
|
год |
|
|
|||||
Фізична суть коефіцієнту дифузії. Коефіцієнт дифузії показує, яка кількість речовини продифундує через поверхню в один метр квадратний протягом одиниці часу (с) при одиничній різниці концентрації на відстань один метр, не залежить від гідродинамічних обставин і наводиться в довідковій літературі.
Турбулентна дифузія
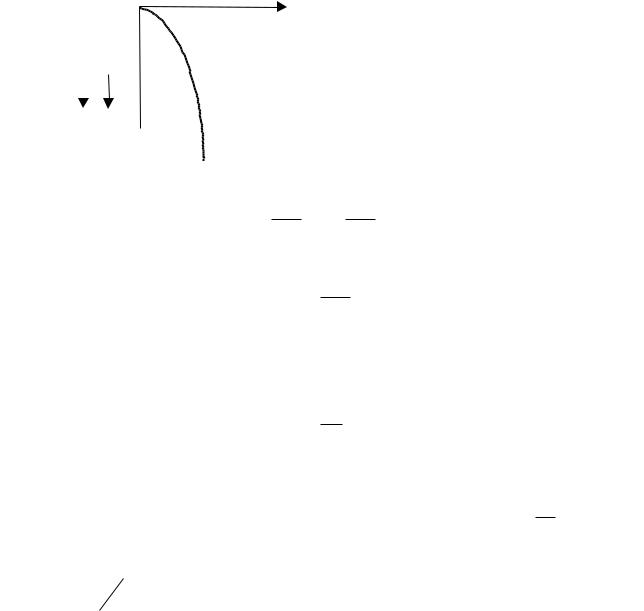
В рухомому середовищі, поряд з ламінарним рухом, має місце також і турбулентна течія середовища. При ламінарному русі має місце молекулярний перенос, при якому спостерігається тільки повздовжний перенос як кількості енергії, так і маси речовини. В турбулентному потоці виникає також і поперечний перенос, який призводить до виникнення додаткових дотичних напруг і додаткового переносу речовини. Тобто турбулентна дифузія пов'язана з турбулентністю потоку.
Перенос кількості руху
Y

 Wy1 dx
Wy1 dx  Wx
Wx

 Wy2 X
Wy2 X 
Рис. 17.9 Турбулентна дифузія
Якщо швидкість двох шарів Wy1 i Wy2, на відстані dx є неоднаковою, то різниця швидкості призводить до утворення дотичної напруги:
dWy dWy dx dx
При турбулентному русі виникають вихори, які спричиняють поперечний рух зі швидкістю WХ . Вихори зумовлюють свою дотичну напругу:
T T dWy dx
Тут T – вихровий коефіцієнт турбулентної в'язкості, який залежить від від швидкості потоку, від гідродинамічної обставки і не може бути фізичною константою аналогічно µ.
Перенос енергії в турбулентному потоці
По аналогії з рівнянням молекулярного переносу тепла (рівняння Фурьє) можна записати рівняння переносу густини теплового потоку при наявності турбулентності:
qn T dT dX
де λT - коефіцієнт турбулентної теплопровідності, який залежить не від фізичних властивостей середовища, а від осереднених швидкостей турбулентного потоку, координат, напрямку руху і інших зовнішніх факторів. Інтенсивність переносу тепла за рахунок турбулентної
теплопровідності λT визначається турбулентною температурою провідності, aT CT ,
де аТ – аналог турбулентної дифузії T.
Механізм турбулентного переносу кількості руху та енергії однаковий (теорія Прандтля):
( T vT ) aT 1

Перенос маси в турбулентному потоці
По аналогії з переносом кількості руху і енергії в турбулентному потоці внаслідок турбулентних пульсацій можна записати вираз для кількості маси, що переноситься:
dM T T dcdx dFd
або для потоку маси, де
qT T dcdx ,
звідси
qT MT .
Тут εТ - коефіцієнт вихрової дифузії, який не є фізичною константою, як D, а залежить від гідродинамічної обстановки потоку. Внаслідок аналогії між теплопереносом і масопереносом
вважається, що, T  aT 1. По аналогії з коефіцієнтом молекулярної дифузії εТ - показує, яка
aT 1. По аналогії з коефіцієнтом молекулярної дифузії εТ - показує, яка
кількість речовини переноситься за одиницю часу через одиницю поверхні, при одиничній різниці концентрацій на довжину 1м. εТ характеризує інтенсивність перемішування при масообміні.
Слід відмітити, що з розвитком турбулентності виникає повздовжне перемішування в потоці, що зменшує повздовжній градієнт концентрацій і погіршує масообмін, розділення суміші і перенос розподіленої речовини. Зменшується ефективність масопередачі. Щоб запобігти зменшенню повздовжного вирівнювання концентрацій, застосовують різні технологічні методи (використання дрібної насадки, організація руху потоку і т.д.).
Конвективна дифузія
При потоці, що рухається, маса речовини переноситься як за рахунок молекулярної, так і за рахунок турбулентної дифузії. Загальний перенос речовини можна записати, як:
q q |
|
q |
( D |
|
) |
dc |
(17.16) |
M |
T |
|
|||||
|
T |
|
|
dx |
|
||
|
|
|
|
|
|
|
Сумарний перенос речовини називається конвективною дифузією. Переходячи до кінцевих різниць в виразі (17.16), одержимо:
q ( D |
|
) |
c |
(17.17) |
|
T |
x |
||||
|
|
|
З іншої сторони дифузійний потік із dM= К∆cdF запишеться як: q = К с (17.18)
Прирівнявши праві частини виразів (17.17) і (17.18), одержимо:
K D Tx
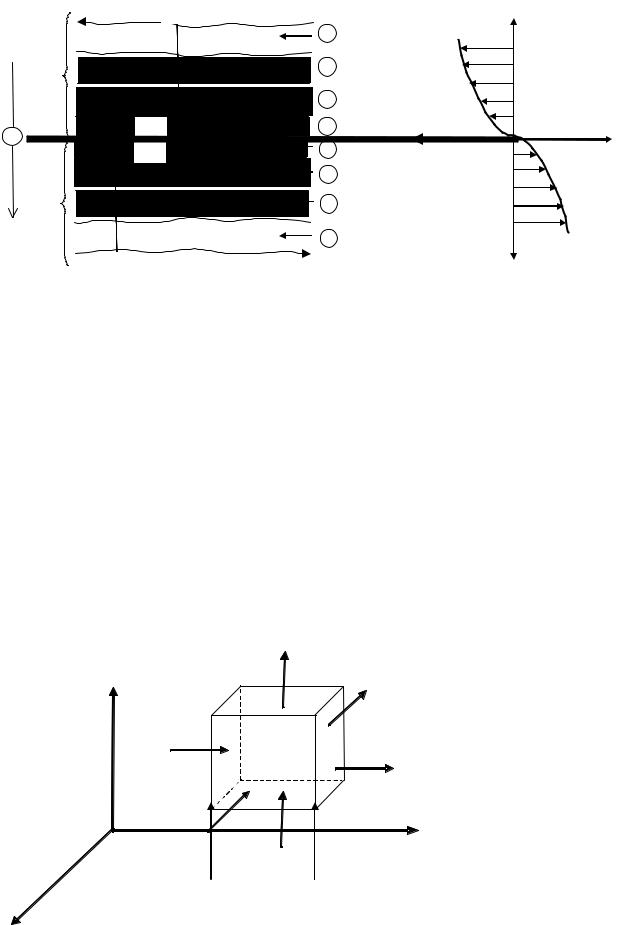
Коефіцієнт масопередачі враховує перенос речовини, як за рахунок молекулярної, так і вихрової дифузії. Таким чином, механізм процесу масопередачі зводиться до молекулярної і конвективної дифузії. Структурна модель процесу масопередачі наведена на рис. 17.10.
|
|
YЯ |
|
|
Фаза G |
|
4 |
|
WY |
|
|
3 |
|
|
|
|
2 |
|
|
|
|
1 |
Y |
M.P.Ф |
|
Yг |
|
||
M |
|
|
||
|
|
|
|
|
|
Хг |
1 |
|
Y |
|
|
|
||
|
|
2 |
|
|
|
|
3 |
|
|
Фаза L |
|
4 |
|
X |
|
|
|
|
ХЯ
Рис. 17.10. Структурна модель процесу масопереносу.
1 – дифузійний прошарок; 2 – в’язкий прошарок; 3 –турбулентний пограничний шар; 4 – ядро потоку.
В ядрі потоку 4 маса цільового компоненту в основному переноситься потоком середовища за рахунок турбулентних пульсацій, молекулярна дифузія присутня, але її роль мінімальна.
З наближенням до дифузійного прошарку 1 перенос маси за рахунок турбулентної дифузії зменшується, і тому збільшується частка маси, перенесеної за рахунок молекулярної дифузії, але ще у в’язкому прошарку 2 основний перенос маси – турбулентний. В дифузійному прошарку маса переноситься в основному за рахунок молекулярної дифузії.
Концентрація цільового компонента в ядрі 4 потоку YЯ постійна. Потім повільно зменшується в турбулентному прошарку 3. У дифузійному прошарку 1 суттєво зменшується. З’являється градієнт концентрацій і підвищується роль молекулярної дифузії.
Диференційні рівняння масопередачі Диференційне рівняння молекулярної дифузії
Розглянемо елементарний об'єм dx, dy, dz в нерухомому середовищі, або в рухомому ламінарному потоці, через ребра якого за час dτ проходить деяка маса речовини.
Нехай через всі три грані входить в даний об'єм , відповідно , Мх, Му, Mz речовини за час dτ,
рис. 17.11.
Z
My+dy
Y |
Mz+dz |
Mx
Mx+dx
X
Mz My
СС+ Cx dx
Рис. 17.11 До виведення диференційного рівняння молекулярної дифузії
Позначимо концентрацію цільового компонента на лівій вертикальній грані – с, а на правій грані вздовж вісі Х з урахуванням зміни концентрація цільового компонента буде
c cx dx , рис. 17.11.
Тоді за час d через поверхню dF=dydz, розташовану перпендикулярно напрямку дифузійного потоку вздовж осі Х кількість речовини, що продифундує до елементарного об’єму згідно першого закону Фіка запишеться, як
Вздовж осі Х:
M x D cx dydzd
Вздовж осі Y:
M y D yc dxdzd
Вздовж осі Z:
M z D cz dxdyd
Через протилежні грані елементарного об’єму, кількості речовини, що виводиться з елементарного об’єму, позначимо: Мх + dx; Му + dy; Мz+ dz.. Тоді вздовж осі Х через грань dydz виходить кількість речовини:
|
|
|
|
( c |
c |
|
|
|
|
|
|
|
|
x |
dx ) |
c dydzd D |
2с dxdydzd . |
||
M |
|
D |
|
|
|
dydzd D |
|||
x dx |
|
x |
|
||||||
|
|
|
|
|
x |
х2 |
|||
Отже, за час dτ в елементі dxdydz збільшується маса речовини на величину вздовж осі Х, яка визначиться за виразом:
|
|
dM |
|
M |
|
M |
|
|
D |
c |
dydzd D |
c |
dydzd D |
2c |
dxdydzd D |
2c |
dxdydzd |
||||||||||||||||||||||||||||||||||||||
|
|
x |
x |
x dx |
x |
x |
x2 |
x2 |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Аналогічно визначається збільшення маси речовини вздовж інших осей в елементарному |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
об’ємі: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
dM |
|
|
M |
|
M |
|
|
|
D |
c |
dydxdzd |
D |
c |
dydxdzd D |
|
2c |
dydxdzd |
D |
|
2c |
dydxdzd |
||||||||||||||||||||||||||||||||
|
|
|
y |
y |
y dy |
y |
y |
y2 |
y2 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
dM |
|
M |
|
M |
|
|
D |
c |
dzdydxd D |
c |
dzdydxd D |
2c |
dzdydxd D |
2c |
dzdydxd |
||||||||||||||||||||||||||||||||||||||||
z |
z |
z dz |
z |
z |
z |
2 |
z |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Тобто, збільшення маси речовини по трьом осям становить : |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
dM = dMx + dMy+ dMz, або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2c |
|
|
2c |
|
|
|
2c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dM D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dxdydzd |
|
|
|
|
|
|
|
|
|
(17.19) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
y |
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
З іншої сторони, за час dτ концентрація зміниться на |
|
величину - |
c |
d |
|
Отже, приріст у |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
елементарному об'ємі дорівнює: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dM dV |
c |
d |
c |
dxdydzd |
|
|
|
|
|
|
|
|
|
|
(17.20) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Прирівнюючи праві частини рівнянь (1.74) і (1.75), отримаємо диференціальне рівняння |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
молекулярної дифузії: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
2c |
|
|
|
|
|
2c |
|
|
2c |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
y |
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
c D 2C

c div( DgradC )
17.10.2 Диференціальне рівняння конвективної дифузії. Другий закон Фіка
Розглянемо перенос речовини за рахунок конвективної дифузії велементарному об'ємі, рис.
17.12.
Y |
|
Wx+ Wx |
|
|
|
||
|
|
|
dx |
|
|
|
x |
|
Wx |
||
М x(к) |
|
|
Мx+dx(к) |
Мx+dx(м) |
|
|
Мx(м) |
|
|
|
|
|
|
|
|
Х
|
C |
C+ С |
|
Z |
x dx |
||
|
Рис. 17.12 До виведення диференційного рівняння конвективної дифузії
Позначимо концентрацію речовини на лівій грані С, тоді на правій грані, з врахуванням приросту концентрації буде: C cx dx (вздовж осі Х), відповідно зміна швидкості потоку
вздовж осі х: на лівій грані: Wx і на правій:Wx wx dx.х
Таким чином, через грань dydz вздовж осі Х, кількість речовини, яка надходить за рахунок конвективного переносу за час dτ дорівнює:
Мх(к)=Wxcdydzdτ
Через праву грань відводиться за рахунок конвективної дифузії кількість речовини: |
|
||||||||||||||||||||
|
|
|
|
|
|
Wx |
|
|
|
c |
|
|
|
|
|
|
|
||||
Mx + dx(к) |
= |
Wx |
|
|
|
|
dx |
c |
|
dx |
|
dydzd |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
cW |
c Wx |
dx W |
c dx |
Wx dx c dx dydzd |
|
|
|
||||||||||||||
|
x |
|
x |
|
|
|
|
|
|
x |
x |
x |
|
|
x |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Приймаємо, що |
Wx |
dx |
c dx 0 , |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
||
Враховуючи, |
|
|
що |
|
|
|
c |
Wx dx W |
x |
c dx |
(Wx c ) dx |
Остаточно |
вираз |
для |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
x |
|
|
|
||
|
c |
(Wx |
|
c ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Mx + dx(к) = Wx |
x |
|
|
|
dx dydzd . |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Зміна маси в елементі вздовж осі X складе:
dM x( к ) M x M x dx( к ) (Wx c ) dxdydzd x
Аналогічно можна записати можна записати зміну маси в елементарному об’ємі вздовж осей
Y і Z.
dM y( к ) (Wy c ) dxdydzd
x
dMz( к ) (Wy c ) dxdydzd
x
Тоді загальна зміна маси в елементарному об’ємі за рахунок конвективної дифузії
запишеться, як: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( w c ) |
|
|
|
( wy c ) |
|
|
( w c ) |
|
|
|
|
|
|
|
||||||||||||||||||
dM=dMx+dMy+dMz= |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
dxdydzd , |
|
|
|||||||||||||
x |
|
|
|
|
|
y |
|
|
|
|
z |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
або в розгорнутому вигляді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
W |
Wу |
|
|
|
|
W |
z |
|
|
|
|
|
|
|
c |
|
|
|
|
|
c |
|
|
c |
|
|
||||||
dM |
|
с |
x |
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
W |
|
|
|
W |
|
dydxdzd |
(17.21) |
||||||||
к |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
y |
|
|
||||||||||||||||||
|
|
x |
|
y |
|
|
|
|
|
z |
|
|
|
|
|
|
|
x |
|
|
|
y |
|
z |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
||||||||||
Для усталеного потоку справедливо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
W |
x |
|
Wу |
|
W |
z |
|
0 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
y |
|
z |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Тоді рівняння (17.21) набуває вигляду: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
dM |
|
|
|
|
|
|
|
|
c |
W |
|
c |
W |
|
c |
|
|
|
|
||||||||||||
|
|
|
|
к |
W |
x |
|
|
|
y |
|
|
z |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|||||||
Кількість цільового компонента, який надходить до елементарного об’єму за рахунок конвективної дифузії, повинна бути відведена через грані елементарного об’єму за рахунок молекулярної дифузії, тобто повинна виконуватись умова:
dM K dM М 0
В іншому випадку концентрація цільового компонента в довільній точці об’єму dV була б змінною в часі, в той час, коли в усталеному процесі вона є тільки функцією координат, тобто
с = f (x, y, z)
Таким чином,
dM М dM К ,
Тобто, виконавши відповідну підстановку, одержимо:
|
2c |
|
2c |
|
2c |
W |
||||
D |
|
2 |
|
2 |
|
2 |
|
|||
|
x |
|
y |
|
z |
|
x |
|||
|
|
|
|
|
|
|
|
|||
або в стислій формі:
D 2c Wgradc
c |
W |
c |
W c |
(17.22) |
x |
|
y y |
z z |
|
Рівняння (17.22) являє собою дифференційне рівняння конвективної дифузії.
Рівняння виражає закон розподілення концентрації цільового компонента при усталеному процесі масообміну.
Для неусталеного процесу масообміну (але здійснюється в умовах стаціонарного руху
фази), коли |
W |
x |
|
Wу |
|
W |
z |
0 , права частина рівняння (17.22) повинна бути доповнена |
c |
, яка |
x |
|
y |
z |
|
|
|||||
|
|
|
|
|
|
|
||||
виражає локальну зміну концентрації в часі. Тоді рівняння (17.22) набуває вигляду: |
|
|
||||||||
|
|
2c |
|
2c |
|
2c |
|
w |
c |
w |
|
c |
w |
c |
|
c |
|||||
|
D |
|
2 |
|
2 |
|
2 |
|
|
|
y |
|
|
|
|||||||
|
|
x |
|
|
y |
|
z |
|
x |
x |
|
y |
z |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
||||||
При масообміні в нерухомому середовищі Wx = Wy = Wz = 0 і рівняння конвективної дифузії |
|||||||||||||||||||||
перетвориться в рівняння молекулярної дифузії |
|
|
|
|
|
|
|
|
|||||||||||||
с |
D 2 c або |
с |
div( Dgrad c ) |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Це рівняння має назву другого закону Фіка.
Термодифузія.
При наявності перепаду температур у фазі виникає перенос маси, зумовлений градієнтом температур, який називається термодифузією.
В цьому випадку більш важкий компонент переміщається в напрямку градієнту температур, тобто в частину об’єму, що має меншу температуру, а більш легкий компонент – в протилежному напрямку. В результаті біля холодної поверхні фаза збагачується більш важким компонентом, а біля

нагрітої – більш легким компонентом. Це явище спостерігається при сушінні і ефективно застосовується при одержанні ізотопів.
Основний закон масовіддачі. Основний закон конвективної дифузії
Основний закон масовіддачі (закон Щукарєва) можна записати так: dM CdFd
Кількість речовини, яка перенесена від ядра потоку, рис. 17.13, до межі розділу фаз, пропорційна різниці концентрацій, поверхні контакту фаз і часу.
Cя
G |
dM |
х |
|
Cг
М.Р.Ф.
Сг'
L |
dM |
у |
Ся'
Рис. 17.13 Схема процесу масовіддачі
β - коефіцієнт масовіддачі:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dM |
|
êã |
|
|
|
ì |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
êã |
|
2 |
|
|
||||||
|
cdFd |
|
ì |
c |
c |
|||||||
|
|
|
ì 3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
Фізична сутність коефіцієнту масовіддачі. Коефіцієнт масовіддачі показує, яка кількість речовини буде перенесена з ядра потоку до межі розділу фаз, або від М.Р.Ф. - в ядро приймаючого потоку, через одиницю поверхні, за одиницю часу при одиничній різниці концентрацій.
Коефіцієнт масовіддачі β характеризує перенос, як за рахунок молекулярної дифузії, так і конвективної. Якщо віднести кількість перенесеної речовини до одиниці часу і вважати процес усталеним, при якому коефіцієнт масовіддачі β=const вздовж поверхні контакту фаз, то рівняння
конвективної дифузії можна записати:
M CF
Якщо провести аналогію з теплообміном, то закон Щукарева аналогічний закону Ньютона для конвективного теплообміну, тобто:
dQ ( tw t f )dFd , або Q tF
Рівняння на межі розділу фаз
Рівняння, яке характеризує умови на межі розділу фаз у фазі G, доповнює диференціальне рівняння конвективної дифузії.
Кількість речовини, яка переноситься із ядра потоку до межи розділу фаз, можна знайти, виходячи з рівняння конвективної дифузії:
dM CdFd |
(17.23) |
Від межі розділу фаз до фази L речовина переноситься за рахунок молекулярної дифузії:
dM D |
c |
dFd |
(17.24) |
|
|||
|
x |
|
|
Оскільки на межі розділу фаз немає накопичення речовини, праві частини рівнянь (17.23) і (17.23) можна прирівняти:
CdFd D cx dFd ,
або
