7 Поняття про м-метод (метод штучного базису)
Вище було викладено алгоритм отримання допустимого базисного рішення у випадку, коли початкове базисне рішення недопустиме. Проте при розрахунку за допомогою симплексних таблиць зручно користуватися так званим М-методом, або методом штучного базису. Він полягає в наступному.
В
кожне рівняння, що дає від'ємну компоненту
в базисному рішенні, вводимо нову
невід'ємну штучну змінну
 ,
яка має той самий знак що і вільний член
в правій частині рівняння. В першій
таблиці включаємо в число основних всі
штучні змінні і ті звичайні додаткові
змінні, які визначають невід'ємні
компоненти базисного рішення. Складаємо
нову лінійну функцію
,
яка має той самий знак що і вільний член
в правій частині рівняння. В першій
таблиці включаємо в число основних всі
штучні змінні і ті звичайні додаткові
змінні, які визначають невід'ємні
компоненти базисного рішення. Складаємо
нову лінійну функцію ,
де М – довільне велике число, і шукаємо
її максимум (Т-задача) назвемо М-функцією
вираз
,
де М – довільне велике число, і шукаємо
її максимум (Т-задача) назвемо М-функцією
вираз .
Справедлива теорема:
.
Справедлива теорема:
Якщо в оптимальному рішенні Т-задачі всі штучні змінні ріні 0, то відповідні значення решти змінних дають оптимальне рішення вихідної задачі (тобто
 ,
якщо
,
якщо ,
тобто мінімум М-функції рівний 0).
,
тобто мінімум М-функції рівний 0).Якщо є оптимальне рішення Т-задачі, в якому хоча б одна зі штучних змінних відмінна від 0, то система обмежена вихідною задачею несумісна.
Якщо
 ,
то вихідна задача також не має розв'язку,
при чому або
,
то вихідна задача також не має розв'язку,
при чому або ,
або умови задачі суперечливі.
,
або умови задачі суперечливі.
Із теореми слідує, що на початку необхідно знайти мінімум М-функції. Якщо він рівний 0 і всі штучні змінні обертаються в 0, то далі можна відкинути ці змінні і вирішувати вихідну задачу, виходячи із отриманого допустимого базисного рішення. На практиці знаходять не мінімум М-функції, а максимум (-М)-функції.
Приклад 7.1. Вирішити задачу 4.1 М-методом, використовуючи симплекс таблиці.
Рішення. Введемо необхідне число штучних змінних і стільки ж додаткових рядків в симплексній таблиці.
Маємо

при обмеженнях:

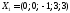 −недопустиме
базисне рішення з однією від'ємною
компонентою, тому в перше рівняння
введемо штучну змінну
−недопустиме
базисне рішення з однією від'ємною
компонентою, тому в перше рівняння
введемо штучну змінну
 з тим самим знаком, що і вільний член:
з тим самим знаком, що і вільний член:

або


Складаємо першу симплекс таблицю (табл. 7.1).
Таблиця 7.1
|
Базис |
Вільний член |
Змінні |
Оціночні відношення | ||||||
|
|
|
|
|
|
|
| |||
|
|
1 |
-1 |
1 |
-1 |
0 |
0 |
1 |
1 | |
|
|
3 |
-1 |
1 |
0 |
1 |
0 |
0 |
3 | |
|
|
3 |
1 |
0 |
0 |
0 |
1 |
0 |
∞ | |
|
|
0 |
-1 |
-2 |
0 |
0 |
0 |
0 |
max | |
|
|
М |
М |
-М |
М |
0 |
0 |
М |
max | |
Останній
рядок – це (-М)-функція, тобто (-МФ)y1.
Заповнюємо її, множачи строку
 на коефіцієнт (-М). перевіряючи виконання
критерію оптимальності при відшуканні
максимуму (-М)-функції, визначаємо, що в
останньому рядку є від'ємний коефіцієнт
в другому стовпчику; це значить, що він
є вирішальним, змінна
на коефіцієнт (-М). перевіряючи виконання
критерію оптимальності при відшуканні
максимуму (-М)-функції, визначаємо, що в
останньому рядку є від'ємний коефіцієнт
в другому стовпчику; це значить, що він
є вирішальним, змінна переходить в основні. Мінімальне оціночне
відношення в першому рядку, він
вирішальний. Змінна
переходить в основні. Мінімальне оціночне
відношення в першому рядку, він
вирішальний. Змінна переходить в неосновні, обертається в
0 на наступному базисному рішенні і далі
виключається з розгляду.
переходить в неосновні, обертається в
0 на наступному базисному рішенні і далі
виключається з розгляду.
У відповідності до загального алгоритму отримуємо табл. 7.2.
Таблиця 7.2
|
Базис |
Вільний член |
Змінні |
Оціночні відношення | |||||
|
|
|
|
|
|
| |||
|
|
1 |
-1 |
1 |
-1 |
0 |
0 |
| |
|
|
2 |
0 |
0 |
1 |
1 |
0 |
| |
|
|
3 |
1 |
0 |
0 |
0 |
1 |
| |
|
|
2 |
-3 |
0 |
-2 |
0 |
0 |
max | |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
max | |
Останній
рядок показує, що критерій оптимальності
виконується;
 ,
означає
,
означає ,
далі цей рядок можна не розглядати.
Отримано допустиме базисне рішення (0;
1; 0; 2; 3), починаючи з якого розв'язуємо
вихідну задачу у відповідності до
звичайного алгоритму.
,
далі цей рядок можна не розглядати.
Отримано допустиме базисне рішення (0;
1; 0; 2; 3), починаючи з якого розв'язуємо
вихідну задачу у відповідності до
звичайного алгоритму.
Список використаної літератури:
Исследование операций в экономике. Учеб. пособие для вузов /Н.Ш.Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. Проф. Н.Ш. Кремера. – М.: ЮНИТИ, 2003. – 407 с.