6 Симплексні таблиці

Практичні розрахунки при рішенні реальних задач симплексним методом виконуються в наш час за допомогою комп’ютерів. Проте якщо розрахунки виконуються без ЕОМ, то зручно використовувати так звані симплексні таблиці. Далі розглянемо алгоритм їх складання, не поглиблюючись в його докладне обґрунтування. Для визначеності вважаємо, що вирішується задача на відшукання максимуму.

І. Після введення додаткових змінних систему рівнянь і лінійну функцію записуємо у вигляді, який називається розширеною системою:

Припускаємо, що всі додаткові змінні мають той самий знак, що і вільні члени; в іншому випадку використовуємо так званий М-метод, який буде розглянуто нижче.

ІІ. Вихідну розширену систему заносимо в першу симплекс таблицю. Останній рядок таблиці, в якому наведено рівняння для лінійної цільової функції, називається оціночним. В ньому вказуються коефіцієнти цільової функції з протилежними знаками: . В лівому стовпчику таблиці записуємо основні змінні (базис), в перший рядок таблиці – всі змінні (відзначаючи при цьому основні), в другому стовпчику – вільні члени розширеної системи. Останній стовпчик підготовлений для оціночних відношень, необхідних при розрахунку найбільш можливого значення змінної. В робочу частину таблиці (починаючи з третього стовпця і третього рядка) занесені коефіцієнтипри змінних з розширеної системи. Далі таблиця перетворюється по певним правилам.

ІІІ. Перевіряємо виконання критерію оптимальності при рішенні задачі на максимум – наявність в останньому рядку від'ємних коефіцієнтів . Якщо таких немає, то рішення оптимальне, досягнутий( в лівому нижньому кутку таблиці), основні змінні приймають значення(другий стовпчик), основні змінні дорівнюють 0, тобто отримуємо оптимальне базисне рішення.

IV. Якщо критерій оптимальності не виконується, то найбільший по модулю від'ємний коефіцієнт в останньому рядку визначає вирішальний стовпчикS.

Складаємо оціночні обмеження кожного рядка за наступними правилами:

1. , якщо і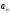мають різні знаки;

2. , якщо і;

3. , якщо ;

4. 0, якщо і;

5. , якщо імають однакові знаки.

Визначаємо . Якщо скінченного мінімуму немає, то задача не має скінченного оптимуму (). Якщо мінімум скінченний, то обираємо рядокq, на якому він досягається (будь-який, якщо їх декілька), і називаємо його вирішальним рядком. На перетині вирішальних стовпчика і рядка знаходиться вирішальний елемент .

V. Переходимо до наступної таблиці за правилами:

а) в лівому стовпці записуємо новий базис: замість основної змінної - змінну;

б) в стовпцях, що відповідають основним змінним, проставляємо нулі і одиниці: 1 – навпроти «своєї» основної змінної, 0 – навпроти «чужої» основної змінної, 0 – в останньому рядку для усіх основних змінних;

в) новий рядок з номером q отримуємо зі старого діленням на вирішальний елемент ; г) усі інші елементивизначаємо за правилом прямокутника:

Далі переходимо до п. ІІІ алгоритму.

Приклад 6.1. Розв’язати задачу про використання ресурсів, наведену у прикладі 2.1 за допомогою симплекс-таблиць.

Рішення. Розширена система задачі має вигляд:

Лінійну функцію представимо у вигляді .

Заповняємо першу симплексну таблицю (табл. 6.2), в якій змінні ,,,основні. Останній рядок заповнюється коефіцієнтами лінійної функції з протилежними знаками (див. п. ІІ алгоритму).

Таблиця 6.2

Базис	Вільний член	Змінні							Оціночні відношення
	18	1	3	1	0	0	0	18/3
	16	2	1	0	1	0	0	16
	5	0	1	0	0	1	0	5
	21	3	0	0	0	0	1	∞
F	0	-2	-3	0	0	0	0

У відповідності до п. ІІІ алгоритму перевіряємо критерій оптимальності. В останньому рядку є від'ємні коефіцієнти. Обираємо з них найбільший по модулю (-3); другий стовпчик вирішальний, змінна перейде в основні (цей стовпець виділено). У відповідності з п.IV знаходимо оціночні відношення і . Третій рядок є вирішальним (виділено). На перетині вирішального стовпця і рядка стоїть вирішальний елемент.

Будуємо табл. 6.3 по правилам п. V алгоритму:

а) в новому базисі основні змінні: ,,,;

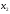б) розставляємо нулі і одиниці; наприклад, в клітинці, що відповідає основній змінній по стовпцю і рядку, ставимо 1, а в клітинці, що відповідає основній зміннійпо рядку, а основній змінній- по стовпцю, ставимо 0 а т.д. В останньому рядку навпроти усіх основних змінних ставимо 0. Третій рядок отримуємо діленням на вирішальний елемент. Решту клітинок заповнюємо по правилу прямокутника. Наприклад:

і т.д.

Отримаємо другу симплекс таблицю (табл. 6.3).

Таблиця 6.3

Базис	Вільний член	Змінні							Оціночні відношення
	3	1	0	1	0	-3	0	3
	11	2	0	0	1	-1	0	11/2
	5	0	1	0	0	1	0	∞
	21	3	0	0	0	0	1	7
F	15	-2	0	0	0	3	0

Критерій оптимальності знову не виконаний. Тепер перший стовпчик вирішальний; 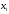- переходить в основні,4 перший рядок вирішальний,- вирішальний елемент.

Нова симплексна таблиця має вид табл. 6.4.

Таблиця 6.4

Базис	Вільний член	Змінні							Оціночні відношення
	3	1	0	1	0	-3	0	∞
	5	0	0	-2	1	5	0	5/5
	5	0	1	0	0	1	0	5/1
	12	0	0	-3	0	9	1	12/9
F	21	0	0	2	0	-3	0

І на цей раз критерій оптимальності не виконаний; п’ятий стовпець і другий рядок вирішальні, - вирішальний елемент.

Переходимо до табл. 6.5.

Таблиця 6.5

Базис	Вільний член	Змінні							Оціночні відношення
	6	1	0	-1/5	3/5	0	0
	1	0	0	-2/5	1/5	1	0
	4	0	1	2/5	-1/5	0	0
	3	0	0	3/5	-9/5	0	1
F	24	0	0	4/5	3/5	0	0

Критерій оптимальності виконується, це означає , оптимальне базисне рішення (6; 4; 0; 0; 1; 3) співпадає з раніше отриманим (див. рішення задачі 2.1 симплексним методом).