Передаточная функция, временные характеристики.
№1
Передаточная функция системы – это:
1. Отношение изображения по Лапласу входного сигнала к изображению выходного при нулевых начальных условиях
2. Произведение изображений по Лапласу входного и выходного сигналов при нулевых начальных условиях
*3. Отношение изображения по Лапласу выходного сигнала к изображению входного при нулевых начальных условиях
4. Отношение изображения по Лапласу входного сигнала к изображению выходного при ненулевых начальных условиях
№2
Передаточная функция системы зависит:
1. Только от параметров входного сигнала.* 2. Только от структуры и параметров системы.
3. И от вида входного сигнала и от структуры и параметров системы.
4. Не зависит ни от входного сигнала, ни от структуры и параметров системы.
№3
Дифференциальное уравнение системы имеет вид
.
и
соответственно вход и выход системы.
Передаточная функция данной системы
имеет вид:
1.
.*2.
.
3.
.
4.
.
№4
Дифференциальное
уравнение САУ имеет вид
,
-
вход,
- выход системы,
.
Передаточная функция САУ имеет вид:
1.
.
2.
.
3.
*4.
.
№5
Дифференциальное
уравнение САУ имеет вид
,
-
вход,
- выход системы,
.
Передаточная функция САУ имеет вид:
1.
.
2.
.
3.
.*4.
.
№6
Передаточная
функция имеет вид
,
- выходной сигнал,
-
входной сигнал. Соответствующее
дифференциальное уравнение имеет вид:
1.
.
* 2.
.
3.
.
4.
.
№7
При последовательном
соединении звеньев с передаточными
функциями
эквивалентная передаточная функция
равна:
*1.
.
2.
.
3.
.
4.
.
№8
При параллельном
соединении звеньев с передаточными
функциями
эквивалентная передаточная функция
равна:
1.
.
*2.
.
3.
.
4.
.
№9
Передаточная
функция имеет вид
,
- выходной сигнал,
-
входной сигнал,
.
Соответствующее дифференциальное
уравнение имеет вид:
*1.
.
2.
3.
4.
№10
Передаточная функция разомкнутой САУ имеет вид:
.
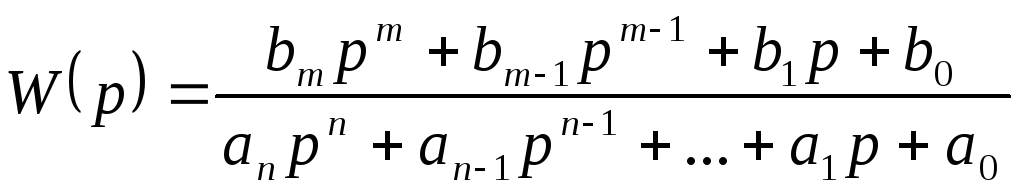Для того, чтобы система обладала
астатизмом первого порядка должно
выполняться условие:
*1.
.
2.
.
3.
.
4.
.
№11
Передаточная
функция разомкнутой САУ имеет вид
.
Чему равен коэффициент передачи
разомкнутой САУ:
1. 2 2. 0,2 3. 10 4. 5
№12
Дифференциальное
уравнение САУ имеет вид
,
- входной сигнал,
.
Передаточная функция САУ имеет вид:
*1.
3.
2.
4.
.
№13
Имеем замкнутую
систему с единичной отрицательной
обратной связью.
- передаточная функция разомкнутой
системы. Передаточная функция замкнутой
системы по задающему воздействию
определяется выражением:
*1.
3.
2.
4.
.
№14
Имеем замкнутую
систему с положительной единичной
обратной связью.
- передаточная функция разомкнутой
системы. Передаточная функция замкнутой
системы по задающему воздействию
определяется выражением:
*1.
3.
2.
4.
.
№15
Имеем замкнутую
систему с отрицательной единичной
обратной связью.
- передаточная функция разомкнутой
системы. Передаточная функция замкнутой
системы по ошибке
определяется выражением:
1.
*
3.
2.
4.
.
№16
Имеем замкнутую
систему с положительной единичной
обратной связью.
- передаточная функция разомкнутой
системы. Передаточная функция замкнутой
системы по ошибке
определяется выражением:
1.
3.
*2.
4.
.
№17
Передаточная
функция разомкнутой САУ имеет вид
.
Чему равен порядок астатизма данной
системы:
*1. 2 3. 3 2. 0 4.1.
№18
Дифференциальное
уравнение системы имеет вид
.
Здесь
- задающее воздействие,
- возмущающее воздействие. Передаточная
функция системы по задающему воздействию
определяется выражением:
1.
3.
2.
4.
.
№19
Эквивалентная передаточная функция соединения
имеет вид:
1.
3.
2.
*4.
.
№20
Эквивалентная передаточная функция соединения
имеет вид:
1.
3.
2.
4.
.
№21
Эквивалентная передаточная функция соединения
имеет вид:
1.
3.
2.
*4.
.
№22
Структурная схема замкнутой системы имеет вид
.
Передаточная
функция замкнутой системы по возмущающему
воздействию
имеет вид:
1.
3.
*2.
4.
.
№23
Переходная функция
звена
- это:
*1. Переходный
процесс на выходе звена при подаче на
его вход функции
и нулевых начальных условиях.
2. Переходный
процесс на выходе звена при подаче на
его вход функции
и нулевых начальных условиях.
3. Переходный процесс на выходе звена в отсутствие входного сигнала при единичных начальных условиях.
4. Переходный
процесс на выходе звена при подаче на
его вход единичного импульса
и нулевых начальных условиях.
№24
Импульсная
переходная функция звена
- это:
1. Переходный
процесс на выходе звена при подаче на
его вход функции
и нулевых начальных условиях.
*2. Переходный
процесс на выходе звена при подаче на
его вход функции
и нулевых начальных условиях.
3. Переходный процесс на выходе звена в отсутствие входного сигнала при единичных начальных условиях.
4. Переходный
процесс на выходе звена при подаче на
его вход единичного импульса
и нулевых начальных условиях.
№25
Весовая характеристика звена – это другое название:
1. Передаточной функции. *3. Импульсной переходной функции.
2. Переходной функции. 4. Дельта-функции.
№26
Связь между
импульсной переходной функцией
и переходной функцией
определяется
зависимостью:
1.
*3.
2.
4.
№27
Связь между
переходной функцией
и импульсной переходной функцией
определяется зависимостью:
1.
3.
2.
4.
.
№28
Связь между
передаточной функцией звена
и его импульсной переходной функцией
определяется уравнением:
1.
3.
2.
*4.
.
№29
Связь между
передаточной функцией звена
и его переходной функцией
определяется уравнением:
1.
3.
*
2.
4.
.
№30
Переходная
характеристика безынерционного звена
с передаточной функцией
определяется выражением:
1.
*3.
2.
4.
.
№31
Импульсная
переходная функция безынерционного
звена с передаточной функцией
определяется выражением:
1.
3.
*2.
4.
.
№32
Переходная
характеристика интегрирующего звена
с передаточной функцией
определяется выражением:
1.
3.
2.
*4.
h(t)=Kt
№33
Импульсная
переходная функция интегрирующего
звена с передаточной функцией
определяется выражением:
1.
3.
2.
*4.
.
№34
Импульсная
переходная функция звена с передаточной
функцией
определяется выражением:
1.
3.
*2
.
4.
.
№35
Переходная функция
звена с передаточной функцией
определяется выражением:
1.
3.
2.
*4.
.
№36
Два звена с
импульсными переходными функциями
и
образуют последовательное соединение.
Импульсная переходная функция
всего соединения связана с импульсными
переходными функциями
и
следующим образом:
*1.
.
2.
3.
.
4.
.
№37
Два звена с
импульсными переходными функциями
и
образуют параллельное соединение.
Импульсная переходная функция
всего соединения связана с импульсными
переходными функциями
и
следующим образом:
1.
.
*2.
3.
.
4.
.
№38
Импульсная
переходная функция звена с передаточной
функцией
определяется выражением:
1.
3.
2.
4.
.
№39
Переходная
характеристика звена с передаточной
функцией
определяется выражением:
1.
3.
2.
4.
.
№40
В линейной системе:
ее передаточная функция,
- соответственно входной и выходной
сигналы,
-
переходная характеристика,
-
импульсная переходная функция. Начальные
условия нулевые. Какое из уравнений
правильно отражает связь между
и
:
1.
3.
2.
4.
.
№41
В линейной системе:
ее передаточная функция,
- соответственно входной и выходной
сигналы,
-
переходная характеристика,
-
импульсная переходная функция. Начальные
условия нулевые. Какое из уравнений
правильно отражает связь между введенными
характеристиками:
1.
3.
2.
4.
.
№42
Переходная
характеристика звена с передаточной
функцией
определяется выражением:
1.
3.
2.
4.
.
№43
Импульсная
переходная функция звена с передаточной
функцией
определяется выражением:
1.
3.
2.
4.
.
№44
В линейной системе:
ее передаточная функция,
- соответственно входной и выходной
сигналы,
-
переходная характеристика,
-
импульсная переходная функция. Начальные
условия нулевые. Какое из уравнений
правильно отражает связь между введенными
характеристиками:
1.
3.
2.
4.
.
№45
Переходная
характеристика звена с передаточной
функцией
имеет вид:
1.
3.
2.
4.
.
№46
Переходная
характеристика звена с передаточной
функцией
имеет вид:
1.
3.
2.
4.
.