Лекція № Плоский напружений стан

Плоский напружений стан виникає у випадку, коли два головних напруження не дорівнюють нулю, а третє дорівнює нулю.

Нехай ,,

Проведемо перерізи І-І, ІІ-ІІ, ІІІ-ІІІ, ІV-IV

Виділимо площадку α – переріз І-І, та β – переріз ІІ-ІІ. Переріз І-І провели під кутом β нормаль .Площадки (α) і (β) перпендикулярні.

Напруження іна площадці α будуть визиватись як дією, так і дією. Тоді застосовуючи принцип суперпозиції, тобто розглядаючи цей плоский напружений стан як накладання двох ортогональних одновісних напружених станів, можемо записати:

=

Де і-напруження, що спричинені дією; аі- напруження, що спричиняються дією.

З формул для лінійного напруженого стану:

;

Для визначенняівраховуємо, щоутворює з напруженнямкут. Тоді

знак так як відрахунок ведеться за годинниковою стрілкою. Тоді

;

Використавши додавання остаточно знайдемо :

На площадці ІІ-ІІ проведем нормаль . НормальУтворює з напрямомкут.

Тоді:

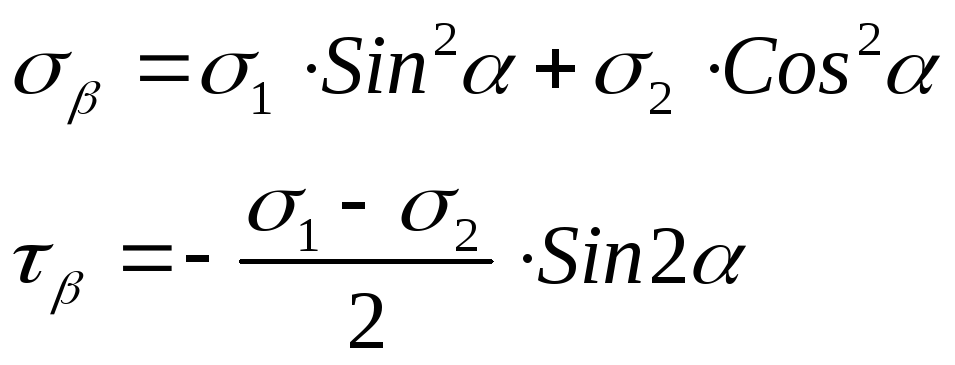
З цих рівнянь маємо, що:

─сума нормальних напружень по двох взаємно перпендикулярних площадках не залежить від кута нахилу цих площадок і дорівнює сумі головних напружень.

─ця рівність виражає закон парності дотичних напружень.

Максимальне дотичне напруження: ,.

В теорії плоско напруженого стану можна розмежувати дві основні задачі: пряма і зворотна.

Пряма задача. В точці відомі положення головних площадок, і відповідні до них головні напруження. Треба знайти нормальні і дотичні напруження, що діють на площадках, які нахилені під заданим кутом до головних;

Зворотня задача. В точці відомі нормалі й дотичні напруження, що діють у двох взаємно перпендикулярних площадках, що походять через дану точку. Треба знайти головні площадки та головні напруження.

Формули для обчислень:

Лекція №

Деформації при об’ємному напруженному стані. Узагальнений закон Гука

Досліджуючи деформації й розглядаючи питання міцності при об’ємному та плоскому напружених станах, будемо відповідно до основних гіпотез та припущень вважати, що матеріал відповідає закону Гука, а деформації малі.

Відносна поздовжня деформація: (1)

а відносна поперечна деформація: (2)

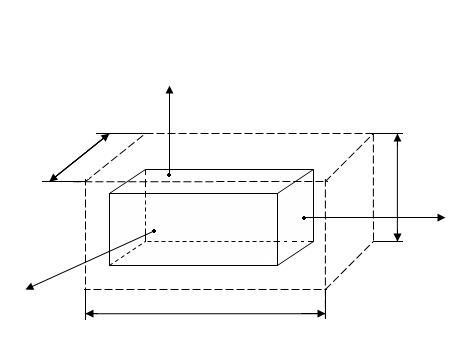
Розглянемо деформацію елемента тіла

c+Δc

с

b

_a

a+Δa

Внаслідок деформації ребра елемента змінюють свою довжину й дорівнюють:

a+Δa; b+Δb; c+Δc.

Величини:

Називаються головними подовженнями і являють собою відносні подовження в головних напрямах.

Застосовуючи принцип суперпозиції, можна записати: , де

- відносне подовження в напружені , спричинене тільки на при .

- відносне подовження в тому самому напрямі, спричинене дією тільки

- подовження спричинене дією

Оскільки напрям самого напруження є поздовжнім, а для напруженьта – поперечним, то застосовуючи формули (1), (2) знаходимо, що

; ;

Склавши ці величини, матимемо

Аналогічно

Це узагальнений закон Гука для ізотропного тіла

Для плоского напруженого стану

;

Критерій найбільш нормальних напружень з трьох головних напружень враховує тільки одне – найбільше, вважаючи, що два інших не впливають ні міцність

Недоліки: Ця теорія дає задовільні результати тільки для дуже крихких матеріалів (камінь, цегла, кераміка, інструментальна сталь). Ця теорія не відображує перехід до пластичного стану.

Об’ємна деформація:

Нехай до деформації елемент займав об’єм . У деформованому стані його об’єм

;

Враховуючи узагальнений закон Гука

;

Можна ввести величину - модуль об’ємної деформації.

Потенціальна енергія деформації:

Потенціальною деформацією деформації називається енергія, що накопичується в тілі при його пружному деформуванні. Для стержня питома потенціальна енергія, тобто енергія, яка припадає на одиницю об’єму.

;

враховуючи, що , матимемо

Для об’ємного напруженого стану

;

При деформуванні елемента взагалі змінюється як його об’єм, так і форма(він з кубика перетворюється на паралелепіпед).

;

- питома потенціальна енергія зміни об’єму

- питома потенціальна енергія формозміни, та енергія яка накопичується внаслідок зміни форми елемента.

;

Критерії міцності (теорії міцності):

І. Критерій найбільших нормальних напружень.

Припускається, що руйнування матеріалу в загальному випадку напруженого стану виникає тоді, коли найбільше нормальне напруження досягає небезпечного значення . Останнє визначають при простому розтяганні або стисканні зразків з даного матеріалу

;

; , где ;