110

Лекция № 23

Тема: Ошибка в САУ.

План лекции:

1. Ошибка при движении с постоянной скоростью.

2. Ошибка при движении с постоянным ускорением.

3. Ошибка при гармоническом задающем воздействии.

Ошибка при движении с постоянной скоростью.

Пусть задающее воздействие изменяется с постоянной скоростью

f=vt , v=const .

Возмущающее воздействие постоянно . В этом случае

Относительно составляющей е₂ остается справедливым все сказанное ранее . Рассмотрим составляющую е₁ . Ранее было показано ,что :

е₁ =∞ , если W(p) – статическая передаточная функция ;

е₁=const≠0 , если W(p) имеет астатизм первого порядка;

е₁=0 , если W(p) имеет астатизм второго и выше порядков .

Таким образом , необходимо рассмотреть только случай , когда передаточная функция W(p) имеет астатизм 1-ог порядка . В этом случае

и при этом W^*(0)=1. Тогда

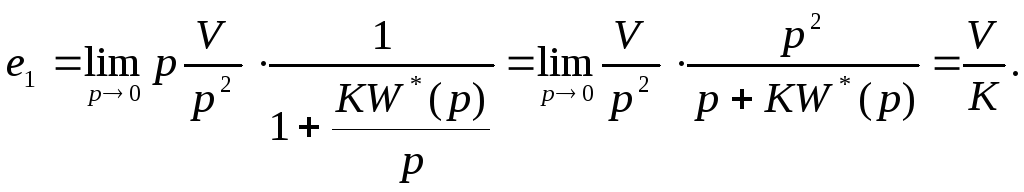(85)

Из ( ) видно , что величина составляющей е₁ установившейся ошибки пропорциональна скорости изменения задающего воздействия и обратного пропорциональна коэффициенту передачи разомкнутой системы по скорости К.

Ошибка при движении с постоянным ускорением.

В этом режиме f(t)=dt² , d – ускорение входного сигнала . Возмущающее воздействие g(t) предполагается постоянным и тогда составляющая е₂ та же , что и в первых случаях.

Рассмотрим составляющую е₁ . очевидно , что , если :

W(p) – статическая передаточная функция или передаточная функция или передаточная функция с астатизмом 1-ог порядка – е₁=∞ ;

W(p) – передаточная функция с астатизмом 2-ог порядка , то е₁=const≠0;

W(p) имеет астатизм 3-ог и выше порядков , то е₁=0.

Поэтому остается рассмотреть только случай астатизма 2-го порядка.

При этом имеем

и

Ошибка при гармоническом задающем воздействии.

Этот режим движения рассматривается часто, т.к. он позволяет достаточно полно оценить динамические свойства САУ. Задающее воздействие имеет вид

f(t)=A sin wt .

Возмущающее воздействие рассматривать не будем (если оно постоянное , то все сказанное выше относительно составляющей е₂ полностью переноситься на этот случай .

Рассмотрим составляющую ошибки , определяемую наличием задающего воздействия . Имеем

В линейной системе при гармоническом входном сигнале ошибка изменяется по гармоническому закону , т.е.

Точность САУ может быть оценена по амплитуде ошибки А_е ; определяемой выражением

Обычно А_е много меньше амплитуды задающего воздействия А , т.е. - большая величина. Тогда

и

(86)

Зависимостью ( ) определяем амплитуду сигнала ошибки при гармоническом входном сигнале и оно же позволяет решить обратную задачу , т.е. сформировать требование к ЛАФЧХ разомкнутой системы , при выполнении которых амплитуда А_е не превосходит заданной величины ∆m. Имеем из (86)

(87)

откуда

и

Значения (w, 20lg) определяет точку на плоскости ЛАЧХ разомкнутой системы . Для выполнения условия (87) ЛАЧХ системы должна проходить выше этой точки (см. рис.82).

Р ис.82.