3.3 Взаимопринадлежность точки и прямой плоскости. Прямые особого положения.

Из положения геометрии следует:

1) прямая принадлежит плоскости, если она проходит черездве точки, принадлежащие данной плоскости.

2) прямая принадлежит плоскости, если она проходит через точку, принадлежащую данной плоскости, и параллельна прямой, находящейся в этой плоскости или параллельна ей. Зададим плоскость  двумя пересекающимися прямыми АВ и СВ (рис.3.10), плоскость  двумя параллельными прямыми DE и FG. Согласно первому положению прямая, пересекающая прямые, определяющие плоскость, находится в данной плоскости. Из этого следует, что если тоскость задана следами, то прямая принадлежит плоскости, если следы прямой находятся на одноименных с ними следах плоскости (рис, 3.11).

25

Рис.3.10

Рис.3.11 Рис.3.12

Плоскости  и  заданы следами (рис.3.11, 3.12).

Прямая, проходящая через точки М и N, пересекает следы плоскостей  и . Точка М является горизонтальным следом прямой MN, точка N - фронтальный след прямой MN и, следовательно, прямая MN принадлежит плоскости  (рис.3.11) и плоскости  (рис. 3.12).

26

Из рис. 3.13 следует, что прямая принадлежит плоскости,

если она параллельна одному из следов этой плоскости и имеет с другим следом общую точку, которая является одноименным следом этой прямой.

Для построения на чертеже точки, лежащей в заданной плоскости, сначала строят прямую, принадлежащую заданной плоскости, затем на этой прямой берут точку.

Например, требуется найти фронтальную проекцию точки D и известно, что точка D принадлежит плоскости, заданной треугольником АВС (рис. 3,14). Сначала строят горизонтальную проекцию прямой,принадлежащей данной плоскости и проходящей через D'. Затем строят фронтальную проекцию той же прямой (А"М") и на ее продлении находят D".

Среди прямых, принадлежащих плоскости, особое положение занимают горизонтали, фронтали и линии наибольшего наклона к плоскостям проекций.

Горизонталями плоскости называют прямые, лежагцие в ней и параллельные горизонтальной плоскости проекций.

Построим горизонталь плоскости, заданной треугольником АВС. Горизонталь построим через вершину А (рис.3.15).

Рис3.14

Рис.3.15 Рис.3.16

Так как горизонталь плоскости параллельна плоскости Н, то ее фронтальная проекция А"К" параллельна оси X, Строим горизонтальную проекцию точки К и проводим прямую через точки А и К.

27

Рассмотрим построение горизонтали плоскости, заданной следами (рис. 3.16).

Горизонтальный след плоскости является одной из ее горизонталей (нулевая горизонталь). Поэтому построение какой -либо из ее горизонталей сводится к проведению в этой плоскости прямой, параллельной горизонтальному следу плоскости.

Горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости; фронтальная проекция горизонтали параллельна оси X.

Фронталями плоскости называют прямые, лежащие в ней и параллельные плоскости проекций V. Пример построения фронтали в плоскости дан на рис.3.17. Построение выполнено

аналогично

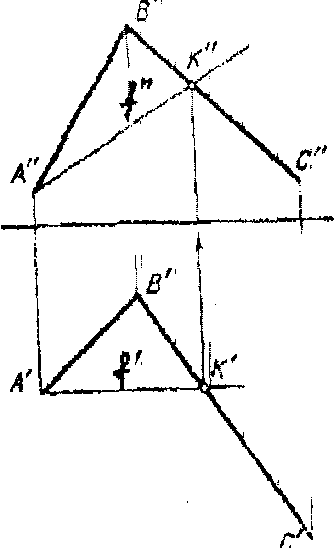
Рис3.17 Рис.3.18

построению горизонтали (см. рис. 3,15), Пусть фронталь проходит через точку А. Так как фронталь параллельна плоскости V, то А'К' параллельна оси X, затем строим фронтальную проекцию К" и фронтальную проекцию фронтали А"К",

Построим фронталь плоскости, заданной следами. Рассматривая рис.3.18 устанавливаем, что прямая MB является фронталью плоскости , она параллельна фронтальному следу (нулевой фронтали) плоскости. Горизонтальная проекция фронтали параллельна оси X, фронтальная проекция фронтали параллельна фронтальному следу плоскости v.

Линиями наибольшего наклона плоскости к плоскостям проекций Н, V, W называются прямые, лежащие в ней, и перпендикулярные или к горизонтали плоскости, или к ее фронтали,

28

или к ее профильной прямой. Линия наибольшего наклона к плоскости Н называется линией ската плоскости,

Эти линии определяют угол наклона плоскости к плоскостями,H,V,W.

Согласно правилам проецирования прямого угла горизонтальная проекция линии ската плоскости перпендикулярна к горизонтальной проекции горизонтали этой плоскости или к ее горизонтальному следу. Фронтальная проекция линии ската строится после построения горизонтальной.

Рис. 3.19 Рис. 3.20

На рис. 3.19 изображена линия ската плоскости : ВК  h, BKB' - линейный угол двугранного угла, образованного этой плоскостью и плоскостью Н. Следовательно линия ската служит для определения угла наклона этой плоскости к плоскости Н.

На рис,3,20 построены линии ската в заданных плоскостях.

Линейный угол между линией ската и ее горизонтальной проекцией равен углу наклона заданной плоскости к плоскости Н.

Линейный угол между линией наибольшего наклона к плоскости V и ее фронтальной проекцией равен углу наклона заданой плоскости к плоскости V.

Линейный угол между линией наибольшего наклона к плоскости W и ее профильной проекцией равен углу наклона заданной плоскости к плоскости W.

29