
- •Министерство образования Российской Федерации
- •Введение
- •В 1798 году французский инженер Гаспар Монж опубликовал свой труд, «Начертательная геометрия» который лег в основу проекционного черчения.
- •1. Виды проецирования
- •1.1. Параллельное проецирование
- •1.3. Проецирование точки на две плоскости проекции
- •1.4. Расположение точек на комплексном чертеже
- •1.5.Проецирование точки на три плоскости проекции
- •2. Проецирование отрезка прямой линии
- •2.1 Проецирование прямой линии на две и три плоскости проекции.
- •2.2.Положение прямой линии относительно плоскостипроекции
- •Прямая, параллельная фронтальной плоскости проекции на-
- •2.3.Взаимное положение двух прямых на комплексном чертеже
- •2.4.Построение на чертеже натуральной величины отрезка прямой общего положения и углов наклона прямой к плоскостям проекций
- •2.5. Точка на прямой. Проецирование прямого угла. Следы прямой.
- •3. Плоскость
- •3.1 Задание и изображение плоскости на чертеже
- •3.2 Следы плоскости
- •3.3 Взаимопринадлежность точки и прямой плоскости. Прямые особого положения.
- •3.4 Положение плоскостей относительно плоскостей проекций
- •2. Если плоскость перпендикулярна к одной из плоскостей
- •3.5.1. Пересечение прямой линии с плоскостью, перпендикулярной к одной или двум плоскостям проекций
- •3.6. Построение линии пересечения двух плоскостей
- •3.7.Пересечение прямой линии с плоскостью общего положения
- •3.8. Пересечение двух плоскостей общего положения
- •3.9. Построение линии пересечения двух плоскостей по точкам пресечения прямых линий с плоскостью
- •4. Способы преобразования чертежа
- •4.1 Способ перемены плоскостей проекций
- •4.1.1. Введение в систему н, V одной дополнительной плоскости проекции
- •4.1.2.Введение в систему h.V двух дополнительных плоскостей проекций
- •4.2.Способ вращения вокруг оси, перпендикулярной к плоскости проекций
- •4.2.1.Вращение вокруг заданной оси
- •4.2.2.Вращение вокруг выбранной оси
- •4.3. Способ параллельного перемещения
- •5.Поверхность. Определение, задание и изображение начертеже. Определитель поверхности. Принадлежность точки и линии поверхности. Построение линии пересечения поверхностей.
- •5.1. Гранные поверхности.
- •Призмы и пирамиды в трех проекциях, точки на поверхности
- •5.2.Поверхсности вращения
- •5.3.Точка и линия на поверхности
- •5.4.0Бщие сведения о способах построения линии взаимного пересечения двух поверхностей
- •5.5.Пересечение поверхностей, когда одна из них проецирующая
- •5.6. Способ вспомогательных секущих плоскостей
- •Рис 5.14
- •5.7.Способ вспомогательных секущих сфер с постоянным центром
- •5.8. Некоторые особые случаи пересечения поверхностей
- •5.8.1. Пересечение поверхностей, описанных вокруг одной сферы
- •6.1.Общие сведения о пересечении поверхности плоскостью.
- •6.2.Пересечение пирамиды с плоскостью
- •6.3. Пересечение призмы с плоскостью
- •6.4. Пересечение цилиндра с плоскостью
- •6.5. Пересечение конуса с плоскостью
- •Рис 6.7
- •6.6. Пересечение сферы с плоскостью
- •6.7. Пересечение тора с плоскостью
- •6.8. Примеры построения чертежей деталей, усеченных проецирующими плоскостями
- •7. Метрические задачи
- •7.1 Определение действительной величины плоского угла но его ортогональным проекциям
- •7.2 Перпендикулярность прямых, прямой и плосксти. Перпендикулярность плоскостей
- •7.2.1 Взаимно перпендикулярные прямые.
- •7.2.2.Взаимно перпендикулярные прямая и плоскость
- •7.2.3. Взаимно перпендикулярные плоскости
- •7.4.2.Параллельность прямой и плоскости
- •7.4.3.Параллельность плоскостей
- •7.5.0Пределение действительной величины отрезка по его ортогональным проекциям
- •7.6.0Пределение расстояния между точкой и прямой. Между двумя параллельными прямыми
- •7.7.Определение расстояния от точки до плоскости, между плоскостями
- •8. Развертки поверхностей. Развертки гранных поверхностей и поверхностей вращения
- •8.1,Способ нормальных сечений
- •8.2.Способ раскатки
- •8.3.Способ триангуляции (способ треугольников)
- •9. Аксонометрические проекции
- •9.1. Общие сведения
- •9.2. Показатели искажения
- •9.3. Стандартные аксонометрические проекции
- •9.3.1. Прямоугольная изометрическая проекция
- •9.3.2. Прямоугольная диметрическая проекция
- •9.3.3. Косоугольные аксонометрические проекции
- •9.4. Аксонометрические проекции окружности
- •9.4.1. Окружность в прямоугольной изометрии
- •9.4.2. Окружность в прямоугольной диметрии
- •9.4.3. Окружность в косоугольной фронтальной диметрии
- •9.5. Примеры построения стандартных аксонометрий
- •10. Машинная графика
- •131 Список литературы
- •132 Содержание
Прямая, параллельная фронтальной плоскости проекции на-
зывается фронталью – f (рис.2.4), (y-const).

Рис. 2.4.
14
Профильная прямая р- прямая параллельная профильной плоскости проекции W (x-const), рис. 2.5.
Профильная проекция отрезка прямой равна самому отрезку E'"F"'= EF; E'F' параллельна оси у; E"F" параллельна оси z. Проецирующими прямыми - называются такие прямые,
которые перпендикулярные плоскостям проекций (рис. 2.6, 2.7, 2.8). Прямая, перпендикулярная к фронтальной плоскости проекции, называется фронтально - проецирующей прямой (рис.2.6),
Фронтальная проекция отрезка прямой равна самому отрезку
(C'D"= CD).
C'D' параллельна оси х.
C '"D'"
параллельна оси z.
'"D'"
параллельна оси z.

Рис. 2.5.
Рис. 2.6.
Прямая перпендикулярная к горизонтальной плоскости проекции называется горизонтально - проецирующая прямая
(рис.2.7).
Рис. 2.7.
15
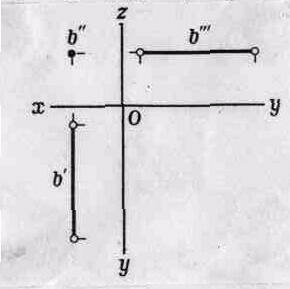
Прямая перпендикулярная к профильной плоскости проекции называется профильно - проецирующая прямая (рис.2.8).

Рис. 2.8.
2.3.Взаимное положение двух прямых на комплексном чертеже
Если через данную точку А требуется провести прямую, параллельную данной прямой LМ,то построение сводится к проведннию через точку А прямой, параллельной L"M", и через точку А' прямой параллельной L'M', рис.2.9 а.


16
В случае, изображенном на рис.2.9 б, параллельные прямые расположены в общей для них проецирующей плоскости, перпендикулярной к пл.Н, Поэтому горизонтальные проекции этихпрямых расположены на одной прямой.
Если прямые пересекаются в точке К, то их проекции тоже пересекаются, при этом проекции точки К' и К" расположены на одном перпендикуляре (рис.2.10).
Действительно, если точка К принадлежит обеим прямым АВ и CD, то проекция этой точки должна быть точкой пересечения проекций данных прямых,
З аключение
о том, что данные на чертеже прямые
пересекаются между собой, можно сделать
всегда по отношению к пря-мым общего
положения, независимо от того, даны ли
проекциина трех или двух плоскостях
проекций, необходимым и достаточным
условием является лишь то, чтобы точки
пересечения одноименных проекций
находились на одном и том же перпендикуляре
к соответствующей оси проекций (рис.2.11)
или. на чертеже без оси проекций
(рис.2,12), эти точки оказались бы налинии
связи установленного для нее направления.
Но если однаиз данных прямых параллельна
какой- либо из плоскостей проекций, а
на чертеже не даны проекции на этой
плоскости, тонельзя утверждать, что
такие прямые пересекаются между со-бой,
хотя бы и было соблюдено указанное выше
условие, на-пример, в случае, данном на
рис.2.13, прямые АВ иCD,
из ко-торых прямая CD
параллельна плоскости W,
не пересекаются между собой; это может
быть подтверждено построением профильных
проекций или применением правила о
делении отрез-ков в данном отношении.
аключение
о том, что данные на чертеже прямые
пересекаются между собой, можно сделать
всегда по отношению к пря-мым общего
положения, независимо от того, даны ли
проекциина трех или двух плоскостях
проекций, необходимым и достаточным
условием является лишь то, чтобы точки
пересечения одноименных проекций
находились на одном и том же перпендикуляре
к соответствующей оси проекций (рис.2.11)
или. на чертеже без оси проекций
(рис.2,12), эти точки оказались бы налинии
связи установленного для нее направления.
Но если однаиз данных прямых параллельна
какой- либо из плоскостей проекций, а
на чертеже не даны проекции на этой
плоскости, тонельзя утверждать, что
такие прямые пересекаются между со-бой,
хотя бы и было соблюдено указанное выше
условие, на-пример, в случае, данном на
рис.2.13, прямые АВ иCD,
из ко-торых прямая CD
параллельна плоскости W,
не пересекаются между собой; это может
быть подтверждено построением профильных
проекций или применением правила о
делении отрез-ков в данном отношении.
Рис.2.10
Рис.2.11


а) б)
Рис.2.9
17
Если точка пересечения npoeкцuu прямых не расположены на одном перпендикуляре к оси х, то прямые скрещиваются (рис.2.14).
На рис.2.14, 2.15 изображены две скрещивающиеся прямые общего положения: хотя одноименные проекции и пересекаются между собой, но точки их пересечения не могут быть соединены линией связи, то есть прямые не пересекаются между собой.

Рис.2.13. Рис.2.14 Рис. 2.15
