9. Аксонометрические проекции

9.1. Общие сведения

Во многих случаях при выполнении технических чертежей оказывается необходимым наряду с комплексным чертежом оригинала давать более наглядное изображение, обладающее свойством обратимости.

С этой целью применяют чертеж, состоящий только из одной параллельной проекции данного оригинала, дополненный проекцией пространственной системы координат, к которой предварительно отнесен изображаемый оригинал. Такой чертеж называется аксонометрическим или аксонометрией. Слово аксонометрия означает «измерение по осям».

Рассмотрим построение аксонометрической проекции. Выберем какую - нибудь плоскость проекций Р и спроецируем на нее по направлению S заданную точку А вместе с осями прямоугольных (натуральных) координат, к которым она отнесена в пространстве (рис 9.1 ). Плоскость Р называют тоскостъю аксонометрических проекций (эту плоскость называют также картинной плоскостью).

Проекция А' называется аксонометрической проекцией точки А, а точка А₁ - вторичной проекцией точки А, В дальнейшем аксонометрическую проекцию A^/ условимся обозначать так же, как ' в пространстве, буквой А.

111

Проекция OAxA1A называется аксонометрической координатной ломаной..

Отрезки О Ax, Ax А_1 и А ₁А , соответственно параллельные осям х, у и z - аксонометрическими отрезками координат.

Проекция O'x'y'z называется аксонометрической системой координат. Она состоит из аксонометрических осей х, у, z, пересекающихся в точке О', называемой аксонометрическим началом координат.

Проекции х, у, z осей х, у и z называются аксонометрическими осями координат.

Проекции е'я e'y, ё'г натурального масштаба е называются аксонометри ческими масштабами.

9.2. Показатели искажения

Отношения аксонометрических координат к натуральным (при одной и той же натуральной единице е) называются показателями искажения по ослы.

Обозначим через и показатель искажения по оси х, через v - показатель искажения по оси .у, через w - показатель искажения по оси г, тогда

;;

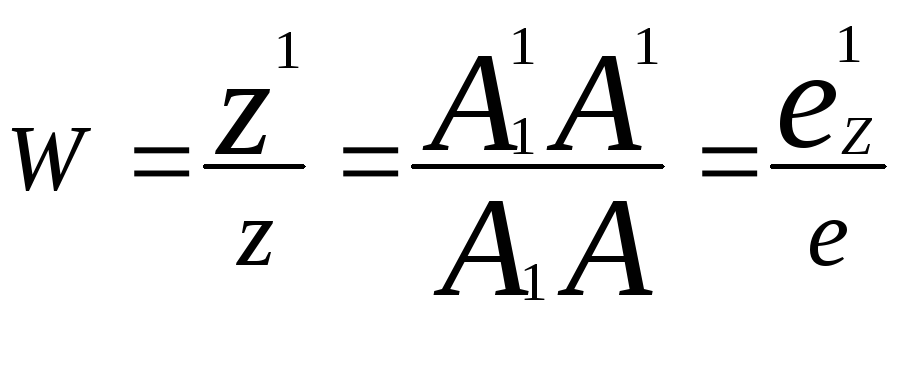
Если все три показателя искажения по осям равны между собой:

и = v = w, то аксонометрическая проекция называется изометрией.

Если два показателя искажения равны между собой и отличаются от третьего показателя, то аксонометрическая проекция называется диметрией. При этом и = v  w, или v = w и, или w = и  v.

Если все три показателя искажения по осям различны; uv; vw, wu, то аксонометрическая проекция называется триметрией.

В зависимости от наклона изображаемого предмета к плоскости аксонометрических проекций и угла, образуемого проецирующими лучами с аксонометрической плоскостью, получают аксонометрические проекции различного типа. Если проецирующие лучи перпендикулярны к плоскости аксонометрических проекций, проекции называют прямоугольными; если проецирующие лучи не перпендикулярны к плоскости аксонометрических проекций, проекции называют косоугольными.

Все виды аксонометрических проекций обладают следующими свойствами:

112

113

- любому чертежу в аксонометрических проекциях должен предшествовать чертеж выполненный в ортогональных проекциях;

- ось г проецируется всегда вертикально;

- все измерения делаются только по осям или параллельно

осям;

- все прямые линии, параллельные между собой или

параллельные осям симметрии на ортогональном чертеже, остаются параллельными в аксонометрии.