1

Доказать выпуклость шара

2

Доказать теорему. Пересечение произвольного числа выпуклых множеств является выпуклым множеством.

3

Доказать утверждение. Многогранное множество выпукло.

4

Основываясь на свойствах вершин, составить алгоритм перебора всех вершин многогранного множества .

5

Доказать теорему. Многогранное множество имеет не более конечного числа вершин

6

Показать, что определение грани размерности 0 совпадает с определением вершины.

7

Пусть имеем следующее ()-мерное множество (называемое ()-мерным симплексом):

.

Определить число граней размерности 1, 2, ..., .

Ответ подать в виде .

8

Определить число граней размерности -мерного параллелепипеда:

.

Ответ подать в виде .

9

Продолжить доказательство Теоремы о представлении многогранника

10

Привести примеры проблемных ситуаций, в которых нарушаются условия аддитивности и пропорциональности.

11

Доказать теорему. Пусть все элементы матрицы и вектора ЗЛП в КФ являются целыми числами и пусть - базисное решение системы . Тогда , где и .

12

Показать, что ДБР обладает всеми свойствами вершины.

13

Показать, что если (в задаче на максимум) в качестве вводимой в базис переменной выбирать переменную такую, что , то при этом не обязательно будет получен максимальный прирост целевой функции. Подобрать «красивый» пример. Дать его графическую иллюстрацию.

14

Для устранения вырожденности задача

заменяется задачей (в вектор b вносятся небольшие «возмущения»)

,

 - достаточно малое.

Тогда, если b() – вектор правых частей и B=- текущий базис, то . (*)

Объяснить почему (*) справедливо.

14

Решить ЗЛП симплекс-методом (НЕ ТАБЛИЧНЫМ!!!) .

В качестве начального ДБР взять выделенную точку.

(Для начальной точки определить все элементы преобразованной задачи.

Если решение не оптимально, то по вектору определить вводимую в базис переменную.

Используя способ перехода от одного ДБР к другому, определить переменную, выводимую их базиса.

Для нового ДБР определить все элементы преобразованной задачи.....

15

У разі наявності альтернативного оптимуму можливі три таких випадки:

1) альтернативний оптимум –(нескінчена) обмежена множина;

2) альтернативний оптимум – (нескінчена) необмежена множина;

3) при наявності ознаки альтернативного оптимуму оптимумальною є єдина точка.

Для кожного випадку

• виписати ознаку;

• показати цю ознаку по симплекс-таблиці;

• дати графічну ілюстрацію.

16

Для ЗЛП

(в лекциях была допущена ошибка: надо заменить на )

для выделенной точки определить структуру симплекс-таблицы:

• множество базисных переменных;

• компоненты вектора (элементы -строки) («+», «-», 0);

• столбцы, соответствующие из небазисным переменных («+», «-», 0).

16

М-метод. Для ЗЛП в канонической форме

,

,

,

,

,

,

построить начальное ДБР. Найти выражение для компонент вектора относительных оценок небазисных переменных. Отдельно выписать выражения для переменных и .

18

Двухэтапный метод. Теорема 2. Если в оптимальном решении задачи

некоторые компоненты вектора отличны от нуля, то исходная задача

не имеет допустимых решений.

17

Двухэтапный метод. Сконструировать и решить пример, иллюстрирующий ситуацию A (нулевая иск. переменная выводится из базиса)

18

Двухэтапный метод. Сконструировать и решить пример, иллюстрирующий ситуацию Б(нулевая иск. переменная не выводится из базиса)

19

Двухэтапный метод. Для ЗЛП

построить начальное ДБР I-го этапа, определить базис, получить выражения для r – строки (компоненты вектора относительных оценок небазисных переменных для вспомогательной задачи) и z – строки (компоненты вектора относительных оценок небазисных переменных для исходной задачи). Отдельно выписать выражения для переменных и .

20

А. Найти начальное ДБР без использования искусственных переменных.

Б. Решить задачу графическим способом.

В. Определить, какой вид должна иметь ЗЛП с числом переменных , чтобы её можно было решить графическим способом.

21

К теме «Модифицированный СМ»

Показать что матрица (используемая для нахождении новой обратной матрицы ) определяется так:

,

где .

(При сдаче уметь находить матрицу для конкретных примеров!!!)

22

К теме «Двойственность в ЛП»

Симметричная пара двойственных задач

Прямая задача

Двойственная задача

Показать, что задача, двойственная к задаче (4)–(6) совпадает с ПЗ (1)–(3).

23

К теме «Двойственность в ЛП»

Несимметричная пара двойственных задач

Прямая задача

Двойственная задача

Показать, что задача, двойственная к задаче (10)–(12) совпадает с задачей (7)–(9). (Не забыть привести задачу (10)–(12) к КФ)

24

К теме «Двойственность в ЛП»

Построить ДЗ для ЗЛП в общей форме:

,

,

,

,

,

.

25

К теме «Двойственность в ЛП»

Часть доказательства Т1

Теорема 1 (основные соотношения двойственности)

Пусть прямая и двойственная задачи имеют допустимые решения. И пусть x и y – это некоторые допустимые решения прямой и двойственной задач соответственно. Тогда справедливо неравенство:

(1)

причём для достижения равенства в (1) необходимо и достаточно выполнение условий:

(2)

26

В доказательстве Следствия 1 Теоремы 1 доказать оптимальность у⁰
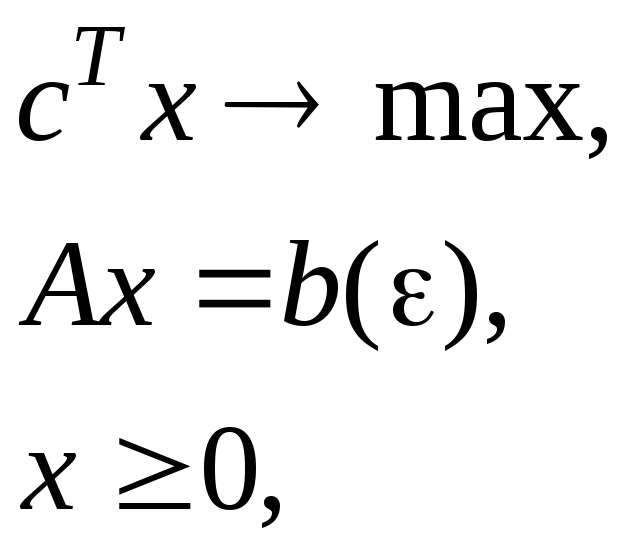
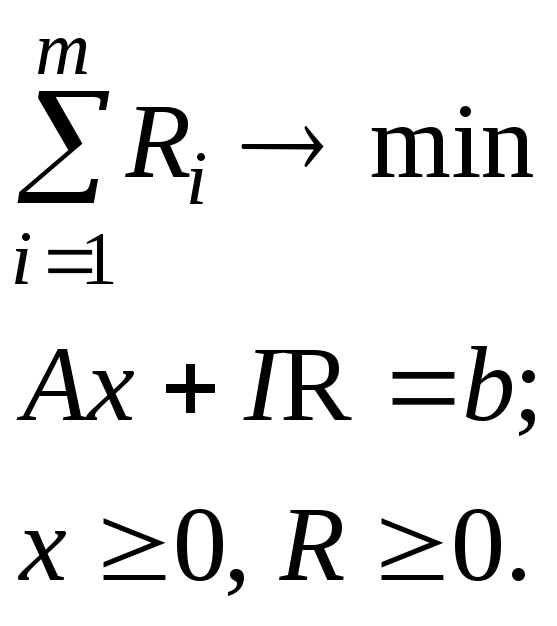