В.В.Воробьев. Теория управления. Нелинейные системы автоматического регулирования и управления. Конс / ЛЕКЦИЯ11

ЛЕКЦИЯ 11: Примеры точечного преобразования.

План.

1. Математическое описание системы.

2. Получение закона точечного преобразования.

3. Диаграмма точечного преобразования.

4. Построение графиков переходных процессов.

5. Применение метода точечного преобразования для системы с релейной характеристикой общего вида.

В качестве первого примера рассмотрим ту же систему, что и при разборе метода припасовывания (лекция 9). Уравнения объекта и регулятора имеют вид

где F(x) — гистерезисная релейная характеристика (рис. 3.10). Эту систему уравнений перепишем в виде

На фазовой плоскости (х, у) нанесем линии переклю­чения, соответствующие заданной нелинейной характери­стике (рис. 3.10): х=b при у > 0, х = -b при у < 0. Это будут полупрямые П0 и П1 (рис. 3.11).

Рис. 3.10

Ввиду нечетной симметрии характеристики F (х) можно рассматривать только участок фазовой траектории QQ1, иду­щий от полупрямой П0 до П1,так как закон возвращения этой траектории к линии П0 будет аналогичен. Таким обра­зом, будем рассматривать точеч­ное преобразование полупрямой П0 в полупрямую П1 (а не саму П0 в себя, как ранее). При этом исходная точка Q имеет последующую Q1.

Пусть в точке Q будет t=0, а в точке Q1 обозначим t=. На участке фазовой траектории QQ1 имеем F(x)= с. Поэтому уравнения (3.17) принимают вид

Интегрирование их дает

Используем здесь параметрический способ точечного преобразования. Обозначим ординаты точек Q и Q1 через у0 и y1 соответственно. Закон точечного преобразования будем искать в виде функций у0() и у1(). При началь­ных условиях (точка Q) t=0, х=b, у=у0 определя­ются произвольные постоянные в (3.18) и (3.19):

В точке Q1 имеем t=, х= -b, у= у1. Подставляя эти величины в уравнение (3.18), получаем

Рис. 3.11.

А подстановка в уравнение (3.19) даёт

Из последнего уравнения непосредственно находим

Тогда из (3.20) с учетом (3.21) получим

Формулы (3.21) и (3.22) и являются искомым законом точечного преобразования в параметрической форме.

Построим диаграмму (рис. 3.12) точечного преобра­зования в виде кривых у0() и у1() - (Переменная у1 берется по абсолютному значению, так как она отрица­тельна). Здесь в одном графике отражено все протекание переходного процесса (обозначено стрелками) и периодическое решение - точка пересечения кривых. При этом в переходном процессе найдены последовательные значе­ния ординат у0 и у1, а также времена  движения на

Рис. 3.12.

Рис. 3.13.

каждом участке, а в периодическом режиме — амплитуда у* и полупериод Т.

На рис. 3.13 показаны точки образующей переходных колебаний, взятые из диаграммы точечных преобразований (рис. 3.12). Дальше эти точки соединяются экспонен­тами (рис. 3.14) согласно уравнению (3.18). Таким образом, в виде единого простого геометрического построения здесь решается вся задача припасовывания решений по

Рис. 3.14.

Рис. 3.15.

участкам для переменной у. Затем, имея длины участков 1, 2, 3, ... и зная, что на границах участков х= ±b, легко по уравнению (3.19) построить также и кривую переходного процесса для переменной х (рис. 3.15, где х*—амплитуда автоколебаний). Аналогично получается и затухающий процесс (выше точки у*, рис. 3.12).

В качестве второго примера возьмем ту же систему (3.17), но с релейной характеристикой общего вида (рис. 3.16). Здесь на фазовой плоскости получаем четыре линии переключения (рис. 3.17).

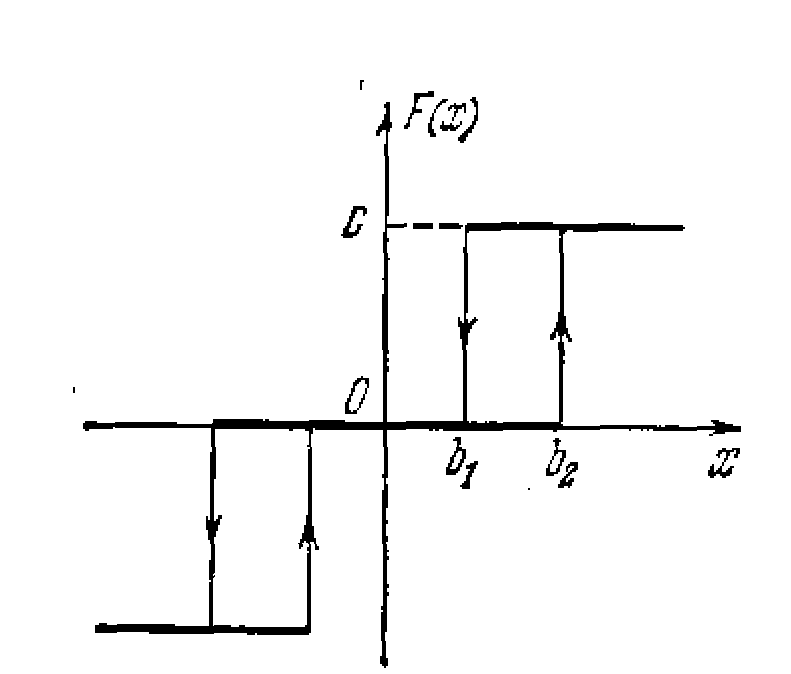
Рис. 3.16.

Рис. 3.17.

Ввиду нечетной сим­метрии характеристики F(x) достаточно рассмотреть участок фазовой траектории QQ1Q2, идущий от линии П0 через П1 до линии П2. При этом часть Q1Q2 фазовой траектории будет прямолинейная, так как там F(х)=0, и в силу (3.17)

Итак, будем рассматривать точечное преобразование полупрямой П0 в полупрямую П2 при условии, что пос­ледующая точка Q2 находится на линии П2. Но суще­ствуют фазовые траектории Q' Q1'Q2' у которых после­дующая точка Q2' находится не на линии П2, а на отрезке –b2<х <b1. Следовательно, надо будет также рассмотреть точечное преобразование части полупрямой П0 и в этот отрезок.

Начнем с первого случая (QQ1Q2). На участке QQ1, где F(x)= с, имеем решения уравнений (3.17) в виде

В силу начальных условий t=0, х= b2, у=у0 находим

В точке Q1 имеем: t = 1, х= b1, у=у1. Поэтому из (3.24) получаем

откуда находим

Используем далее уравнение (3.23) для участка тра­ектории Q1Q2. С учетом начальных условии

найдем произвольную постоянную

В точке Q2 имеем t=, х= -b2, у =у2. Поэтому из (3.23) получаем

или, согласно (3.26),

Мы получили параметрические выражения (через па­раметр 1) ординат исходной у0 (3.25) и последующей у2 (3.30) точек. Это позволяет построить диаграмму точеч­ного преобразования в параметрической форме (рис. 3.18). Параметр 1 в данном случае обозначает не все время движения от Q1 до Q2, а лишь время движения для тра­ектории (QQ1).

Чтобы определить время для всей траектории QQ1Q2, решим первое уравнение (3.17) на участке Q1Q2, где F(х)=0. Получим

Из начальных условий (3.27.) следует

а в точке Q2

Зная из диаграммы (рис. 3.18) значения у2 и 1 для каждого шага точечного преобразования, можем по фор­муле (3.31) подсчитать и время  для этого шага.

Рис. 3.18.

Так определяется переходный процесс, когда точка Q2 находится на линии П2. Предельное (нижнее) положение исходной точки Q0, при котором это справедливо, найдет­ся из диаграммы (рис. 3.18) при , как показано

штриховой линией. Это будет значение . Следовательно, при ординате исходной точки Q выражение (3.30) надо заменить другим. Здесь последующая точка Q2 (рис. 3.17) определяется абсциссой х2. Поскольку в точ­ке имеем у=0, то из (3.23) и (3.28) находим

Следовательно, для каждой точки кривой y0(1), ле­жащей на диаграмме (рис. 3.18) ниже точки берем на оси абсцисс значение 1. Для него но формуле (3.26) вычисляем у1, а затем х2 (3.32). Если при этом окажется , то процесс заканчивается равновесным состоя­нием системы внутри зоны нечувствительности релейной характеристики.