В.В.Воробьев. Теория управления. Нелинейные системы автоматического регулирования и управления. Конс / ЛЕКЦИЯ3

ЛЕКЦИЯ 3. Типы особых точек и фазовые портреты линейных систем.

План.

1. Уравнения, описывающие линейную систему и её фазовые траектории.

2. Случай вещественных корней.

3. Случай равных вещественных корней.

4.Случай комплексных корней.

В качестве исходного материала, используемого в даль­нейшем при изучении нелинейных систем, рассмотрим особые точки линейных систем второго порядка. Уравнения линейной системы имеют вид

или в векторно-матричной форме

при условии, что матрица А невырожденная, т. е. detА0 Дифференциальное уравнение фазовых траек­торий, согласно (1.5), имеет вид

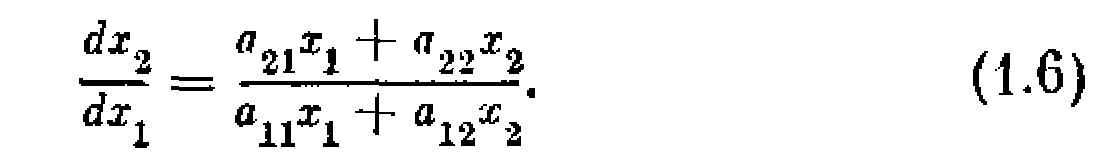
Единственной особой точкой (точкой равновесного состоя­ния системы) является точка х1=0, х2=0.

Пусть корни 1 и 2 характеристического уравнения

(здесь .Е—единичная матрица) различны. Путем подста­новки вида х=Ру где Р — некоторая невырожденная матрица, матрицу А можно привести к диагональному виду. Уравнения (1.5) примут вид:

или

Решением этих уравнений является

Рассмотрим фазовые траектории в этой условной си­стеме координат (у1,у2), а затем отобразим фазовые траектории на плоскость исходных координат (х1,х2).

Случай вещественных корней 1,2 Переходный про­цесс — апериодический. Пусть

Исключив t из решения (1.7), получим уравнение фазо­вых траекторий

Если знаки корней 1,2 одинаковы, то с учетом (1.8) имеем 2/1 > 1, и фазовые траектории представляются в виде парабол, как показано на рис. 1.15. При этом направление движения изображающей точки М по любой фазовой траектории определяется уравнением (1.7), а именно: случаю 1<0, 2< 0 отвечает рис. 1.15,а,

Рис. 1.15.

что соответствует затухающим переходным процессам; случай 1>0, 2> 0 (рис. 1.15,б) соответствует рас­ходящимся переходным процессам. Если же знаки корней 1,2 различны, то в урав­нении (1.9) имеем 2/1<-1, и фазовые траек­тории имеют вид гипер­бол (рис. 1.16).

В случае отрицатель­ных вещественных корней (рис. 1.15, а) особая точ­ка 0 называется точкой типа «устойчивый узел».

В случае положитель­ных вещественных кор­ней (рис. 1.15, б) осо­бая точка 0 называется точкой типа «неустойчи­вый узел».

В случае же вещественных корней разных знаков (рис. 1.16) особая точка 0 называется точкой типа «сед­ло». Седловая точка всегда неустойчива.

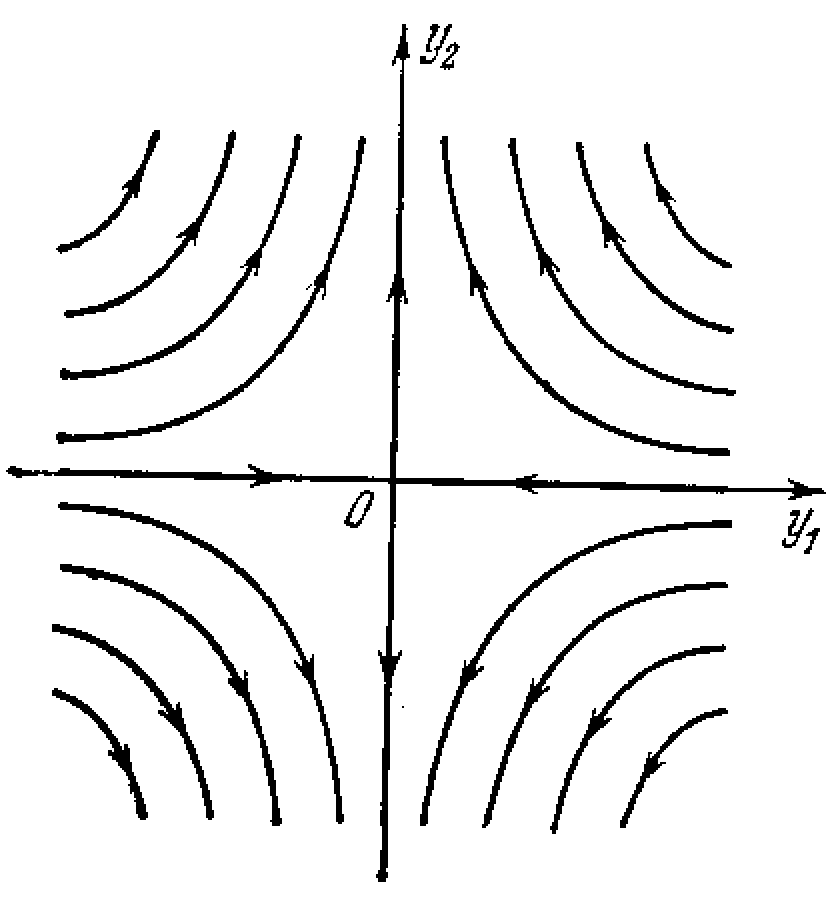
Рис. 1.16.

Отобразим полученные фазовые портреты линейной системы на плоскость исходных координат (х1,х2). Ис­пользуем тот факт, что оси парабол и асимптоты гипер­бол (у1,у2) сами являются фазовыми траекториями и при линейном преобразовании останутся прямыми. Их отображение на плоскость (х1х2) примет вид х2=kx1. Подставив это соотношение в (1.6), получим

или

откуда находим два значения k1 и k2. Это дает две пря­молинейные фазовые траектории (рис. 1.17)^*)*).

Рис. 1.17.

На рис. 1.17 дано расположение также и остальных (криволинейных) фазовых траекторий. Аналогичная картина изображена и на рис. 1.18 для особой точки типа «седло». По какой из фазовых траекторий пойдет переходный про­цесс в системе, определяется начальными условиями х1(t0), х2(t0), которые дают вам координаты начальной точки Мо (рис. 1.17).

Для уточнения такой качественной картины фазовых траекторий можно применить метод изоклин.

Рис. 1.18.

Изоклиной называется линия, соединяющая точки фазовых траекто­рий с одинаковым наклоном касательной, т. е. для каж­дой изоклины dx2/dx1 = с. Поэтому уравнение изоклины, согласно (1.6), имеет вид

Следовательно, любая прямая х2 =kиx1 будет изоклиной с соответствующим значением постоянной с. Задаваясь определенной величиной kи (рис. 1.18), согласно (1.10) находим

Нанеся несколько изоклин и зная для каждой из них крутизну наклона с пересекающих ее фазовых траекто­рии, можно уточнить всю картину фазовых траекторий.

Случай равных вещественных корней: 1=2. В этом случае получается вырожденный узел, устойчивый при 1,2<0 и неустойчивый при 1,2>0 (фазовые траекто­рии показаны в координатах у1, у2 на рис. 1.19, а, б).

Рис. 1.19.

Случай комплексных корней 1,2. Переходный про­цесс — колебательный. Пусть

Решения (1.7) принимают комплексный вид

Введя новые переменные с помощью подстановки

преобразуем решение к вещественной форме

где А и  — произвольные постоянные. Перейдем к полярным координатам (r,). Тогда

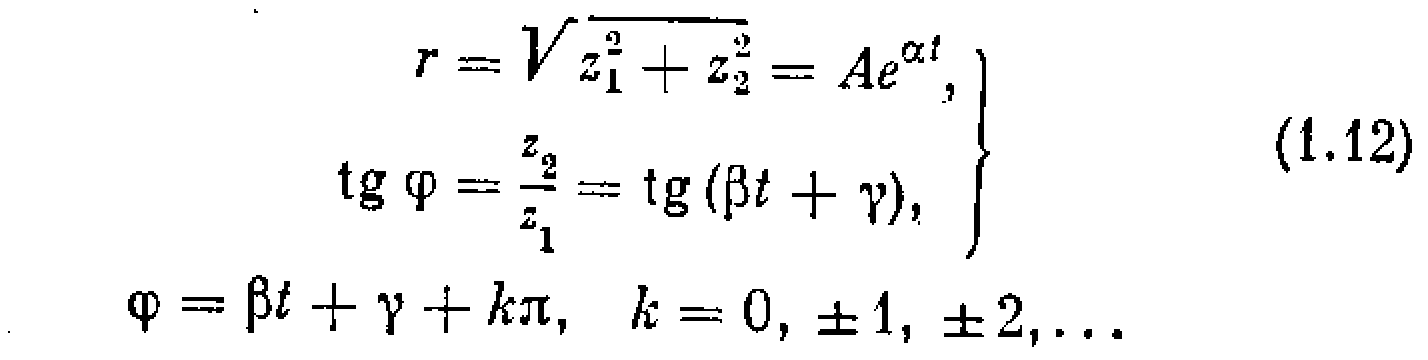
Эти выражения описывают логарифмическую спираль, изображенную на рис. 1.20, а для случая  < 0 и на рис. 1.20, б для  > 0.

Рис. 1.20.

В случае комплексных корней с отрицательной ве­щественной частью (рис. 1.20, а) особая точка 0 называ­ется точкой типа «устойчивый фокус».

В случае комплексных корней с положительной ве­щественной частью (рис. 1.20, б) особая точка 0 называ­ется точкой типа «неустойчивый фокус».

Для преобразования полученных фазовых портретов в исходную систему координат (х1,х2) воспользуемся методом изоклин. Пусть, например, задана система

Корни характеристического уравнения 1,2=-1j2.

Обозначив х == х1, х2 приведем систему к виду

Дифференциальное уравнение фазовых траекторий

Для изоклины х2 = kи х1 отсюда находим

Возьмем четыре значения. kи=0, 1, , -1; тогда с = -, -7, -2, 3. Соответствующие направления касательных

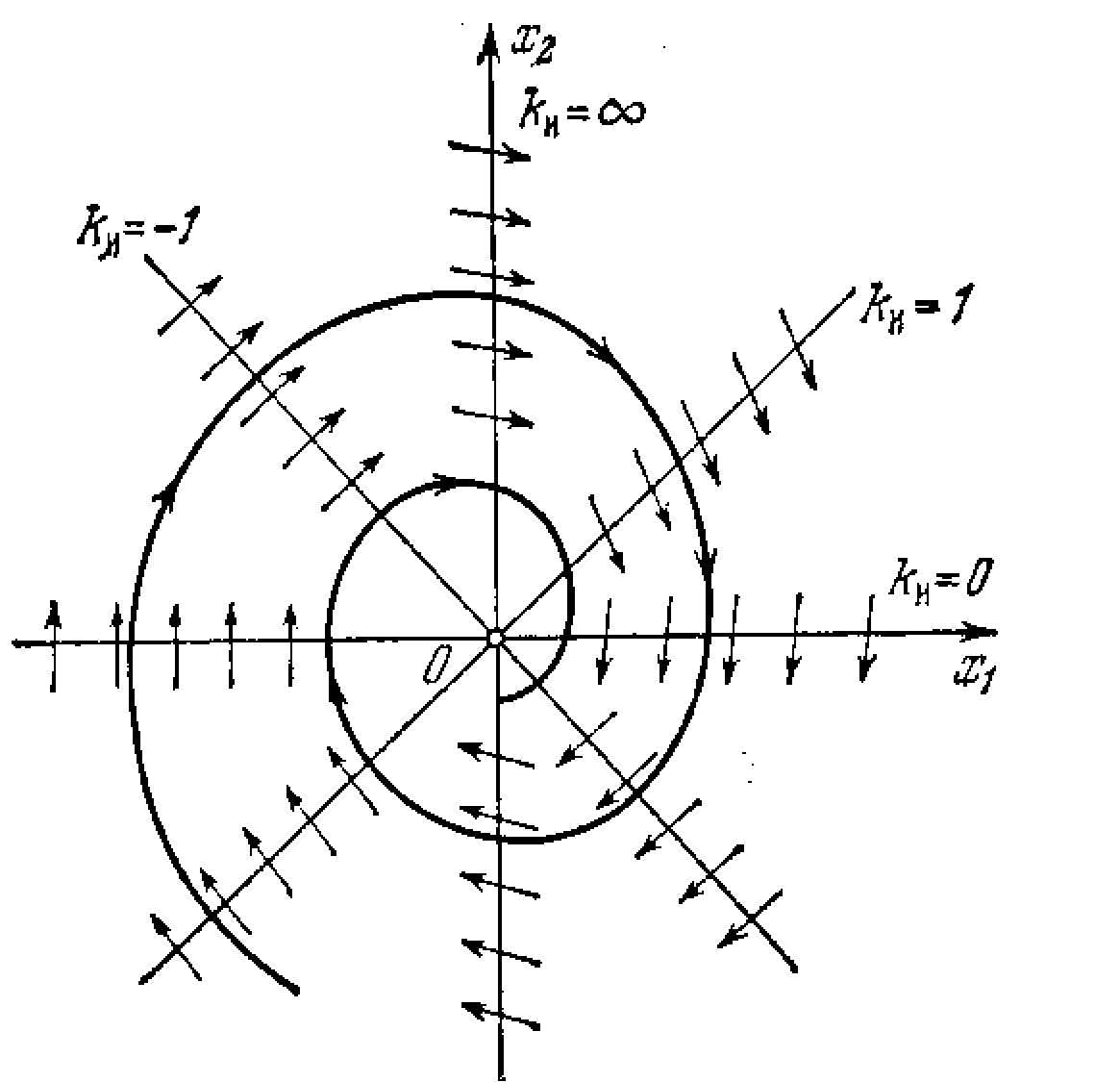
Рис. 1.21.

к фазовым траекториям показаны на рис. 1.21 стрелками. Ориентируясь по ним, вычерчиваем фазовые траектории. Одна из них изображена на рис. 1.21.

Как частный случай (1.11), при  = 0, т. е. для чисто мнимых корней

1,2 = ±j, из (1.12) в полярных координатах на плоскости (z1,z2) получаем

r=A=const. Фазовые траектории имеют вид окружностей (рис. 1.22). При переходе к исходным координатам

Рис. 1.22. Рис. 1.23.

(х1,х2) получатся эллипсовидные замкнутые кривые (рис. 1.23). Это соответствует периодическим во времени процессам. В случае чисто мнимых корней особая точка 0 (рис. 1.22 и 1.23) называется точкой типа «центр».

*) Как и ранее на рисунках коэффициенты k обозначают не углы, а крутизну наклона соответствующих прямых (т.е. k равны тангенсам углов наклона).