В.В.Воробьев. Теория управления. Нелинейные системы автоматического регулирования и управления. Конс / ЛЕКЦИЯ22

ЛЕКЦИЯ 22. Исследование устойчивости методом гармонической линеаризации

План.

1.Определение области устойчивости методом гармонической

линеаризации.

2.Примеры определения границ устойчивости в пространстве параметров нелинейных динамических систем.

Для нелинейных систем с одной нелинейностью, обладающих свойством фильтра (лекция 12), можно определять устойчивость как свойство затухания переходных процессов. Это непосредственно вытекает из материала лекции 13, 14 (см., например, рис. 4.16, 4.18). При этом граница устойчивости может быть определена как граница области существования периодических собственных колебаний в системе (К = Кгр на рис. 4.16, 4.18), т. е. как граница появления пары чисто мнимых корней в характеристическом уравнении гармонически линеаризованной системы. А это в свою очередь можно определить, приравняв нулю предпоследний определитель Гурвица

если все остальные определители положительны (для систем третьего и четвертого порядка это означает просто положительность коэффициентов характеристического уравнения).

Ограничимся рассмотрением однозначных нечетных нелинейностей F(x), гармоническая линеаризация которых имеет вид

F(x) = q(a)x. (5.32)

Величина коэффициента q(а)x, как видно из графиков, полученных в лекции 13, 14, меняется в зависимости от а в различных пределах для различных форм однозначных нелинейностей. Для одних — в пределах

0  q   (5.33)

для других — с некоторыми конечными предельными значениями:

где r1 u г2 — определенные числа для каждой нелинейности (см. лекцию 13, 14). Бесконечный интервал (5.33) охваты­вает все виды однозначных нелинейностей.

Для отыскания границы устойчивости системы (5.31), как границы появления периодических колебаний с какой-либо амплитудой а, надо потребовать выполнения

равенства n-1(q) = 0 хотя бы при каком-либо одном значении q в возможном для данной нелинейности ин­тервале (5.33) или (5.34).

Область же устойчивости системы будет лежать с той стороны этой границы, где

при всех возможных для данной нелинейности значени­ях q. Так, в примере 1 лекции 15, 16 имеем k  q  0 причем граница устойчивости (5.31) получается при q = k, а условие (5.35) выполняется, согласно (4.48), при

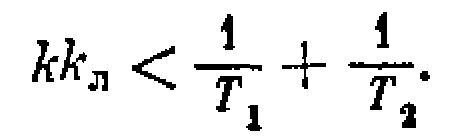
Аналогично в примере 2 лекции 15, 16 имеем 0  q  qmax, qmax=2c/b и граница устойчивости (5.31) достигается при q = qmax, а область устойчивости (5.35)

Если же речь идет об определении абсолютной устойчивости при любой форме однозначной нелинейности, удовлетворяющей лишь условию (5.16), т. е.

F(0) = 0, xF(x) > 0 при х  0, (5.36)

или (5.22) при наличии зоны нечувствительности, то на­до потребовать удовлетворения условия (5.35) при лю­бом значении q в бесконечном интервале (5.33).

Граница (5.31) области абсолютной устойчивости (5.35) определяется обращением в нуль минимально воз­можного при 0  q   значения n-1.Это минимальное значение может получаться как при конечном значении q внутри интервала [0, оо] (рис. 5.14, а), так и при одном из крайних значений q = 0 или q =  (рис. 5,14, б). Иначе говоря, граница устойчивости мо­жет быть определена из пары условий

или

или

Приведем примеры.

Пример 1. В качестве первого примера рассмотрим абсолютную устойчивость той же системы управления курсом самолета (рис. 5.9), которая в лекции 21 исследова­лась методом Ляпунова. Проведя гармоническую линеа­ризацию нелинейности F(u)= q(a)u., получим, согласно

Рис. 5.14.

уравнениям (5.21) — (5.23), характеристическое уравне­ние системы в виде

Условия (5.37) принимают вид

Оба они удовлетворяются при q = 0, если

Это— граница устойчивости (типа (5.38)). Условие же устойчивости n-1 > 0 при любом положительном значении q, как нетрудно видеть, запишется в виде

откуда непосредственно вытекают оба условия (5.30) и оба графика рис. 5.13, полученные методом Ляпунова. Такое совпадение имеет место не только в данном при­мере, но и для большого класса нелинейных систем [22].

Рис. 5.15.

Пример 2. Система (рис. 5.15) задана уравнениями

При замене F(x) = qx получаем характеристическое уравнение

Предпоследний определитель Гурвица

На границе устойчивости, согласно (5.37), имеем

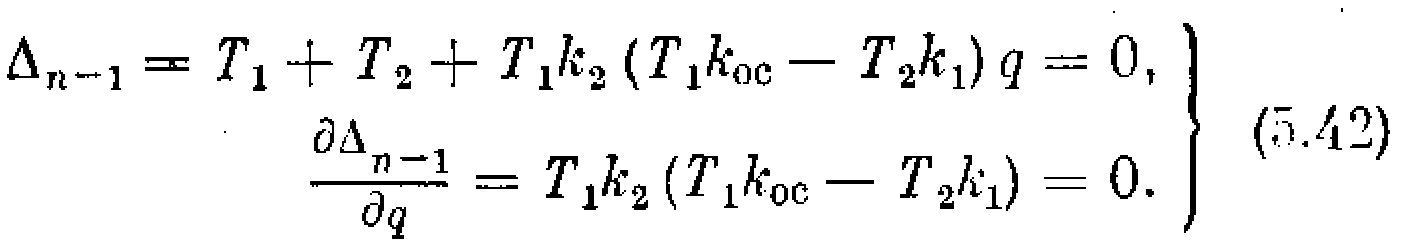
Отсюда - граница абсолютной устойчивости, имеющая место при q=;

В предыдущем примере условие устойчивости опреде­лялось условием (5.38), т. е. q = 0. Здесь же имеет место случай (5.39), т. е. q =. Очевидно далее, что условие абсолютной устойчивости системы n-1 > 0, согласно (5.42), при любом значении q определится неравенством kос >Т2 k1 / T1. В соответствии с этим область устойчиво­сти представлена графически на рис. 5.16.

В [22] имеются примеры, когда условия границы устойчивости (5.37) выполняются не только при край­них значениях q = 0 или q = , как здесь, но при про­межуточных конечных значениях q в соответствии с рис. 5.14. а.

Рис. 5.16.

Рассмотрим теперь влияние конкретной формы нели­нейности на устойчивость нелинейной системы в обоих характерных случаях, приведенных в примерах 1 и 2.

Рис. 5.17.

Пример 3. Пусть в примере 1 задана конкретная форма нелинейности (рис. 5.17, а), для которой коэффи­циент гармонической линеаризации q лежит в интервале

Поскольку граница устойчивости (5.41) определялась наименьшим значением q = 0, то она останется той же и при данной конкретной форме нелинейности. Но здесь следующим образом может быть определена область не­устойчивости системы (в целом).

Равенство n-1 = 0, определяемое формулой (5.40), при q = 0 дает границу устойчивости, а при всех остальных­

Рис.5.18.

значениях q(a) в интер­вале (5.44) равенство (5.40) определяет автоколебания. Но это возможно, согласно (5.40), только при условии

Иначе окажется n-1< 0 при любых значениях q в интерва­ле (5.44), т. е. система не­устойчива.

В результате получаем в данной системе три области (рис. 5.18): устойчивости, автоколебаний и неустойчиво­сти. Здесь граница устойчивости определяется формулой (5.41), а граница неустойчивости, согласно (5.45),

Однако во многих случаях нежелательно входить и в об­ласть автоколебаний. Тогда выбор параметров системы ограничивается областью устойчивости.

Пример 4. Пусть та же конкретная форма нелиней­ности (рис. 5.17, а) фигурирует в примере 2, приведен­ном выше.

Поскольку граница абсолютной устойчивости (5.42) получается при q=, то ограничение значений q ин­тервалом (5.44) расширит область устойчивости. Вместо (5.43) из (5.42) при q = qm получим новую границу

В соответствии с этим область устойчивости при кон­кретной форме нелинейности вместо общего случая (рис. 5.16) расширится, как показано на рис. 5.19. За этой границей имеет место область автоколебаний.

В заключение заметим, что описанное выше исследо­вание устойчивости нелинейной системы методом гармонической

Рис. 5.19.

линеаризации может быть выполнено и с при­влечением критерия Михайлова вместо критерия Гурвица. Подставив в левую часть характеристического урав­нения гармонически линеаризованной системы  = j и выделив вещественную и мнимую части

надо потребовать выполнения критерия Михайлова при всех возможных значениях q (5.33) или (5.34).

Иначе границу устойчивости можно определить как границу области, в которой

Х(, q)=0, Y(, q)=0,

т. е. как границу области существования автоколебаний. Это бывает удобно в более сложных случаях. Пример будет рассмотрен в конце лекциях 30, 31 (пример 4).