В.В.Воробьев. Теория управления. Нелинейные системы автоматического регулирования и управления. Конс / ЛЕКЦИЯ17

ЛЕКЦИЯ 17. Частотный способ определения симметричных автоколебаний.

План.

1.Основные положения частотного способа.

2.Пример следящей системы с релейной характеристикой.

3. Пример следящей системы с петлевой характеристикой.

Базируясь на свойстве фильтра линейной части системы (лекция 12), ищем периодическое решение нелинейной системы (рис. 4.21) на входе нелинейного элемента приближенно в виде

х = a sin t (4.50)

с неизвестными а и . Задана форма нелинейности у=F(x) и передаточная функция линейной части

Производится гармоническая линеаризация нелинейности

что приводит к передаточной функции

Амплитудно-фазовая частотная характеристика разомкнутой цепи системы получает вид

Периодическое решение линеаризованной системы (4.50) получается при наличии в характеристическом уравнении замкнутой системы пары чисто мнимых корней.

Рис.4.21.

А это по критерию Найквиста соответствует прохождению W(j) через точку -1. Следо­вательно, периодическое реше­ние (4.50) определяется равен­ством

или

где

Уравнение (4.51) определяет искомые амплитуду а и частоту  периодического решения. Это уравнение ре­шается графически следующим образом. На комплексной плоскости (U, V) вычерчивается амплитудно-фазовая частотная характеристика линейной части Wл(j) (рис. 4.22), а также обратная амплитудно-фазовая ха­рактеристика нелинейности с обратным знаком -1/Wн (a). Точка В их пересечения (рис. 4.22) и определяет величи­ны а и , причем значение а отсчитывается по кривой -1/Wн (a), а значение  — по кривой Wл (j).

Вместо этого можно пользоваться двумя скалярными уравнениями, вытекающими из (4.51) и (4.52):

которые также определяют две искомые величины а и .

Последними двумя уравнениями удобнее пользоваться в логарифмическом масштабе, привлекая логарифмические­

Рис. 4.22.

частотные характери­стики линейной части. Тогда вместо (4.53) и (4.54) будем иметь следующие два урав­нения:

На рис. 4.23 слева изображены графики левых частей уравнений (4.55) и (4.56), а справа—правых частей этих уравнений. При этом по оси абсцисс слева часто­та  откладывается, как обычно, в логарифмическом масштабе, а справа—амплитуда а в натуральном масш­табе. Решением этих уравнений будут такие значения а и , чтобы при них одновременно соблюдались оба ра­венства: (4.55) и (4.56). Такое решение показано на рис. 4.23 тонкими линиями в виде прямоугольника.

Очевидно, что сразу угадать это решение не удастся. Поэтому делаются попытки, показанные штриховыми линиями. Последние точки этих пробных прямоугольников М1 и М2 не попадают на фазовую характеристику нели­нейности. По если они расположены по обе стороны ха­рактеристики, как на рис. 4.23, то решение находится интерполяцией — путем проведения прямой ММ1.

Нахождение периодического решения .упрощается а случае однозначной нелинейности F(х). Тогда q' = 0 и уравнения (4.55) и (4.56) принимают вид

Решение показано на рис. 4.24.

Рис. 4.23.

Рис. 4.24.

После определения периодического решения надо ис­следовать его устойчивость. Как уже говорилось, перио­дическое решение имеет место в случае, когда амплитудно-фазовая характеристика разомкнутой цепи

проходит через точку -1. Дадим амплитуде отклонение а. Система будет возвращаться к периодическому ре­шению, если при а > 0 колебания затухают, а при а < 0 — расходятся. Следовательно, при а > 0 харак­теристика W(j, а) дол­жна деформироваться (рис. 4.25) так, чтобы при а > 0 критерий устойчивости Найквиста соблюдался, а при а < 0 — нарушался.

Итак требуется, что­бы на данной часто­те  было

Рис. 4.25.

Отсюда следует, что на рис. 4.22 положительный отсчет амплитуды а вдоль кривой -1/Wн (а) должен быть на­правлен изнутри вовне через кривую Wл (j), как там и показано стрелкой. В противном случае периодическое решение неустойчиво.

Рассмотрим примеры.

Пусть в следящей системе (рис. 4.13, а) усилитель имеет релейную характеристику (рис. 4.17, а). Па рис. 4.17, б для нее показан график коэффициента гар­монической линеаризации q(а), причем q’(а) =0. Для определения периодического решения частотным спосо­бом, согласно рис. 4.22, надо исследовать выражение

Из формулы (4.24) получаем для данной нелинейности

График этой функции изображен па рис. 4.26.

Передаточная функция линейной части имеет вид

Рис.4.26.

Амплитудно-фазовая характеристика для нее приведена на рис. 4.27. Функция же -1/Wн (а), являясь в данном слу­чае вещественной (рис. 4.26), укладывается вся на отрица­тельной части вещественной оси (рис. 4.27). При этом на участке изменения амплитуды b  a  b амплитуда отсчи­тывается слева извне внутрь кривой Wл(j), а на участке а > b— в обратную сторону. Следовательно, первая точка пересечения (а1) дает неустой­чивое периодическое решение, а вторая (а2) — устойчивое (ав­токолебания). Это согласуется с прежним решением (пример 2 лекция 15, 16).

Рассмотрим также случай петлевой характеристики реле (рис. 4.28, а) в той же следящей системе (рис. 4.13, а). Амплитудно-фазовая частотная характе­ристика линейной части та же (рис. 4.28, б). Выражение же для кривой –1/Wн(а), согласно (4.52) и (4.23), при­нимает вид

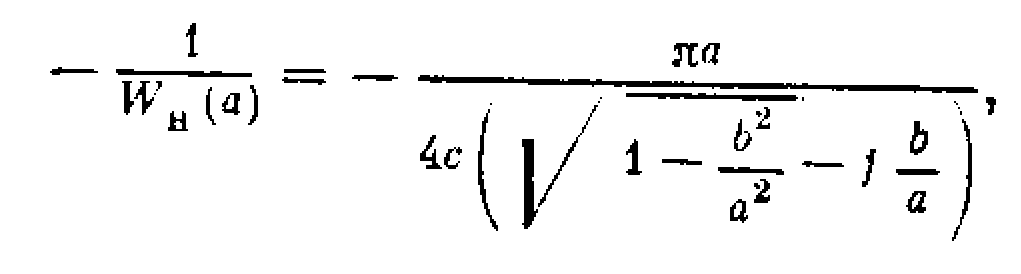
или

Это—прямая, параллельная оси абсцисс (рис. 4.28, б), с отсчетом амплитуды а справа налево. Пересечение даст устойчивое периодическое решение (автоколебания). Чтобы получить графики зависимости амплитуды и частоты

Рис. 4.27.

Рис. 4.28.

от kл, представленные на рис. 4.20, нужно на рис. 4.28 построить серию кривых Wл(j) для каждой величины kл и найти в их точках пересечения с прямой –1/Wн(а) соответствующие значения а и .