В.В.Воробьев. Теория управления. Нелинейные системы автоматического регулирования и управления. Конс / лекция32_33

ЛЕКЦИЯ 32,33. Псевдолинейная коррекция.

План.

1. Псевдолинейные корректирующие устройства.

2. Коррекция апериодического звена.

3. Коррекция инерционности дифференцирующего контура.

4. Нелинейный фильтр с фазовым опережением.

5. Нелинейный фильтр с амплитудным ослаблением.

Псевдолинейными корректирующими устройствами называются такие нелинейные корректирующие устройства, у которых эквивалентные передаточные функции (а значит, и коэффициенты гармонической линеаризации), в отличие от рассмотренных в предыдущей лекции, зависят только от частоты и не зависят от амплитуды. Однако эта зависимость от частоты—нелинейная в том смысле, что характер ее отличается от частотной зависимости линейных передаточных функций и может быть произвольным, т. е. отсутствует жесткая связь меж­ду амплитудными и фазовыми характеристиками, которая имеется у линейных звеньев. Это важное достоинство псевдолинейных устройств позволяет корректировать фазовые соотношения независимо от амплитудных и наоборот, что невозможно сделать линейными средствами.

Результат гармонической линеаризации при исследовании устойчивости для псевдолинейного устройства F(x) имеет вид

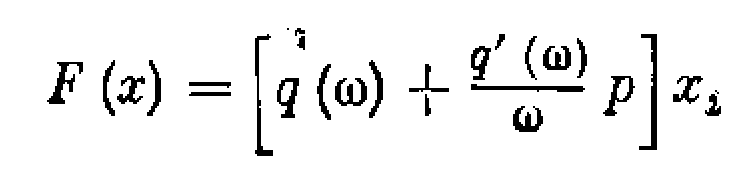
а при исследовании колебательных переходных процессов

Эти выражения можно представить в другой форме:

где для исследования устойчивости имеем

а для колебательных переходных процессов

Такие псевдолинейные корректирующие устройства тоже обладают большими дополнительными возможностями улучшения качества процессов управления по сравнению с линейными устройствами.

Приведем несколько примеров.

1. Коррекция апериодического звена. Ставится задача существенного уменьшения инерцион­ности, т. е. отставания выходного сигнала по

 = arctg Т апериодического звена

(Tp+1) у = kх, (7.32)

В одной из возможных схем такой коррекции (рис. 7.18, а) при помощи ключа отсекаются хвостовые части выходного сигнала, причем последний приобрета­ет форму, показанную штриховкой на рис. 7.18, б. Тогда выражения (4.11) для коэффициентов гармонической ли­неаризации примут вид

где  = arctg Т. Видно, что q и q' будут зависеть лишь от частоты , но не от амплитуды, что характерно для псевдолинейных корректирующих устройств. Применяя другую форму гармонической линеаризации (7.29), получим для скорректированного апериодического звена вместо (7.32) уравнение

в котором новые эквивалентные постоянная времени Т* и коэффициент усиления k* определяются формулами

Рис. 7.18.

(7.30) или (7.31) через найденные уже q() и q’(). На рис. 7.19 приведены графики их зависимости от час­тоты. Видно существенное снижение инерционности (например,

Pис.7.19.

при Т = 2 получается примерно Т* = 0,5Т), но при этом примерно во столько же раз снижается и усиление k*.

Лучший эффект получается при введении дополни­тельного упреждения  (рис. 7.20) при ключевом вырезании части выходного сигнала. При этом получается

Графики для Т* и k* в зависимости от  приоб­ретают вид, показанный на рис. 7.21. Таким способом

Рис.7.21.

можно уменьшать фазовое запаздывание в тех звеньях системы, которые обладают большой постоянной времени, плохо влияющей на качество процесса управления.

2. Коррекция инерционности дифференцирующего контура. Задана схема системы с дифференцирующим контуром F(u) (рис. 7.22), нелинейность которого состоит в коррекции его инерционности.

Рис. 7.22.

Рис. 7.23.

как показано на рис. 7.23. Выходной сигнал, обозначен­ный штриховкой, в хвостовой своей части изменяет знак на противоположный. Тогда вместо линейного диффе­ренцирующего звена

(Tp+1) у = Трu

получаем нелинейное (псевдолинейное) с эквивалентным уравнением

где

 — заданное опережение,  = arctg T. Величина q'

Рис. 7.24

может быть сделана положительной. Зависимость коэф­фициентов гармонической линеаризации q и q' от частоты колебаний  показана на рис. 7.24 при различных заданных опережениях .

Уравнение для ошибки системы (см. рис. 7.22) получает вид

где k = k1 k2 k3 k4 k5. Характеристическое уравнение системы

Частота определяется формулой (после подстановки  = j:

Граница устойчивости n-1 = 0 описывается выражением

Исследование показывает, что область устойчивости системы за счет такой коррекции значительно увеличивается

Рис. 7.25.

т. е. можно существенно повысить общий коэффициент усиления k, не вызывая неустойчивости системы.

3. Нелинейный фильтр с фазовым опере­жением. Схема, показанная на рис. 7.25, позволят получить фазовое опережение без изменения амплитуды. Она аналогична звену переменной структуры, но вместо сложения сигналов введено умножение модуля kx на sign ,

Рис. 7.26.

где —выход линейного фильтра Wф(s), создающего опережение. На рис. 7.26 приведены нелинейные характеристики этой схемы при разных значениях опережения , получаемых выбором параметров схемы. Так, при 0 <  < /2 имеем

а при /2 <  < 

где а - амплитуда входных колебаний, причем при  = /2 точки С1 и С2 сливаются. Если линейная часть фильтра имеет вид

то опережение

Для коэффициентов гармонической линеаризации имеем формулы

причем интегралы разбиваются на два с пределами соот­ветственно (0, ) и (,). В результате получаем

где  = f() выражается формулой (7.34). Как видим, данная нелинейная схема относится к классу псевдоли­нейных. Получаемое фазовое опережение

показано на рис. 7.27 при разных значениях  в зави­симости от частоты , отложенной по логарифмической шкале. При этом амплитудное искажение Q () опреде­ляемое величиной

оказывается незначительным (менее 4 дБ), что вполне приемлемо для решения поставленной задачи.

Рис. 7.27.

Рис. 7.28.

4.Нелинейный фильтр с амплитудным ослаблением. Схема, изображенная на рис. 7.28, позволяет получить ослабление амплитуды с ростом частоты без изменения фазы. Выходной сигнал у = х1х связан с х соотношением

(Тр+1) х1 = sign х.

Формы колебаний входящих сюда переменных при х = a sin t показаны на рис.7.29, причем

где

Используя формулы гармонической линеаризации (7.35), нужно заменить этих формулах kx на х1 и

Рис.7.29.

Рис. 7.30.

разбить каждый интеграл на два: (0, ) и (, ) где  - точка перемены знака х1 (см. рис. 7.29). определяе­мая выражением

Результат интегрирования

(снова отмечаем зависимость q и q' только от частоты, но не от амплитуды). На рис.7.30 показана амплитудная характеристика

такого псевдолинейного фильтра. Из характеристики вид­но эффективное подавление амплитуды колебаний. Лег­ко проверить, что фазовое искажение при этом незначи­тельно.