В.В.Воробьев. Теория управления. Нелинейные системы автоматического регулирования и управления. Конс / лекция26

ЛЕКЦИЯ 26. Процессы управления в автоколебательных системах.

План.

1. Уравнение динамики системы.

2. Коэффициент усиления нелинейности в процессе управления.

3. Определение амплитуды и частоты автоколебаний.

4. Вибрационное сглаживание и вибрационная линеаризация нелинейности при помощи автоколебаний.

5. Влияние автоколебательных вибрационных помех на устойчивость и качество процесса управления.

Автоколебательные системы довольно часто встречаются среди систем автоматического управления и регулирования, в том числе системы с характеристиками релейного типа. Будем считать, что частота автоколебаний в рассматриваемых системах лежит много выше спектра возможных частот процесса управления. Поэтому будем искать решение для переменной х на входе нелинейности (рис. 6.1) в виде

где x°(t) —медленная переменная по сравнению с x*(t). Уравнение динамики системы (рис. 6.1) имеет вид

Q(p) x +R(p) F(x) = S(p) f(t), (6.30)

где f(t) —медленная функция времени (по сравнению с х*). Гармоническую линеаризацию нелинейности произведем в предположении, что х° не успевает заметно измениться за период автоколебаний. Тогда, согласно (4.15),

Подставив (6.31) в уравнение системы (6.30), разобьем последнее, как и прежде, на два. Уравнение для медленных составляющих (т. е. для процесса управления) получит вид

Уравнение для периодических составляющих запишется в виде

Три неизвестных функции x°(t), а и , в искомом решении (6.29) определяются совместным решением уравнений (6.32) и (6.33). Поскольку эти функции взаимосвязаны, причем х° (процесс управления) меняется во времени, то амплитуда а и частота  автоколебаний тоже будут медленно меняться во времени в процессе уп­равления.

Будем рассуждать аналогично нашим рассуждениям в предыдущей лекции. Если путем решения уравнения (6.33) найти зависимость а(х°) и подставить ее в выражение F⁰(х⁰, a), полученное по формуле (4.16), то найдем новую нелинейную функцию

Ф(x⁰) = F°(x⁰, a(x°)),

которая оказывается плавной кривой (рис. 6.8) для лю­бых нелинейностей. Применяя к этой функции всю прежнюю процедуру обычной линеаризации (6.17), (6.18), получим

Для конкретных нелинейностей здесь будут справед­ливы прежние формулы (6.20)—(6.24) и графики (рис. 6.9—6.12), в которых, однако, в отличие от преж­него, величина ас является амплитудой симметричных автоколебаний, определяемой для данной системы со­гласно лекции 15, 16 или 17.

Таким образом, для нахождения коэффициента усиле­ния нелинейности в процессе управления kн в автоколе­бательной системе нет необходимости искать зависимость а (х°) и строить новую нелинейную функцию Ф (х⁰), а требуется знать лишь амплитуду .симметричных авто­колебаний ас. В результате уравнение динамики процес­са управления в автоколебательной системе вместо нели­нейного (6.32) будет линейным:

Однако коэффициент kн обладает особыми свойства­ми. Он, согласно (6.20)—(6.24), зависит от амплитуды ас, а эта последняя, согласно лекции 15,16, определяется через параметры всей системы. Следовательно, kн зависит так­же и от структуры и параметров (ki, Ti) линейной части системы, т. е.

Эту особенность надо учитывать при синтезе системы с использованием линейной теории, а также при исследо­вании устойчивости и качества процессов управления.

Для определения амплитуды и частоты автоколеба­ний, которые накладываются на процесс управления, надо использовать уравнение (6.33). Оно полностью сов­падает с уравнением (4.65) для несимметричных автоко­лебаний. Решается это уравнение в общем случае под­становкой =j в характеристическое уравнение

после выполнения подстановки и выделения веществен­ной и мнимой частей получим два уравнения:

Х(, а, х°) = 0, Y(, а, х⁰) = 0. (6.37)

Отсюда определяются зависимости а(x°) (х⁰) причем x⁰(t)- процесс управления, определяемый дифференциальным уравнением (6.35).

В случае, если нелинейность F(x) является однознач­ной это решение упрощается, так как частота автоколе­баний  в этом случае не зависит от величины х⁰ и от формы нелинейности. Эта частота постоянна в процессе управления и определяется отдельно из уравнения (4.67):

а зависимость а(х°) определяется также отдельно из вы­ражения

куда подставляется значение , найденное из (6.38)

Рис. 6.16.

Пример. Рассмотрим систему с идеальной релейной характеристикой, схема которой приведена на рис. 6.16.

Заданы

и коэффициент жесткой обратной связи kос.

Общее уравнение динамики системы относительно переменной x запишется в виде

Для подстановки и уравнение (6.38) здесь имеем

Поэтому, согласно (6.38), получаем значение частоты автоколебаний

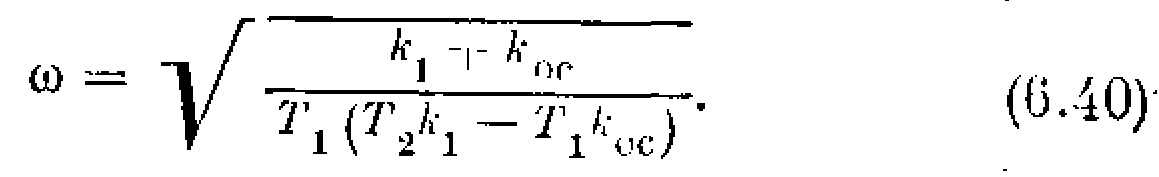
Гармоническая линеаризация нелинейности дает

где, согласно (4.33),

Коэффициент усиления нелинейности в процессе управ­ления Ав, согласно (6.20), вычисляется в виде

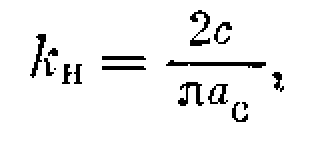
где ас—амплитуда симметричных автоколебаний в дан­ной системе.

Из формул (6.39) и (6.41) при х⁰ = 0 получаем

откуда с подстановкой (6.40) находим

Следовательно,

Итак, общее уравнение динамики системы относи­тельно переменной х для процесса управления принима­ет вид

где коэффициент kн выражается через другие параметры системы формулой (6.43). Дальше эту систему можно рассчитывать как обыкновенную линейную, определяя устойчивость и качество процесса управления с соответ­ствующим выбором параметров, учитывая выражение для kн (6.43). Здесь нужно еще иметь в виду ограничен­ность возможного интервала линеаризации процесса управления, так как из (6.41), например, следует требова­ние х⁰<а. Отсюда вытекают требования на соотношение параметров системы в соответствии с формулой для ам­плитуды (6.42).

Для того чтобы определить амплитуду автоколебаний, наложенных на процесс управления, надо воспользовать­ся формулой (6.39), которая с подстановкой  (6.40) и q (6.41) дает

откуда определяется зависимость а(х°) в процессе управления.

Рис. 6.17.

Рассмотрим и здесь те же две специфические частные задачи, которые рассматривались выше при вынужден­ных вибрациях.

Задача 1. Вибрационное сглаживание и вибрационная линеаризация нелинейности при помощи автоколебании.

Мы видели, что за счет автоколебательных вибраций в автоматической системе любая нелинейная характеристика, в том числе скачкообразная и гистерезисная, становится плавной кривой Ф(х°), как и прежде (рис. 6.8). Это и называется вибрационным сглаживанием нелинейности, а замена Ф⁰ = kн x° — вибрационной линеаризацией нелинейности для сигнала управления при помощи автоколебаний.

Для реализации этого свойства в системе вокруг нелинейного звена организуется внутренний автоколеба­тельный контур (рис. 6.17). Параметры его выбираются так, чтобы частота автоколебаний была достаточно высокой и не пропускалась остальными звеньями системы (за пределами этого контура) и чтобы амплитуда автоколебаний была не меньше возможных значений медленной составляющей х⁰ па входе нелинейности х (рис. 6.17).

Далее вычисляется амплитуда ас симметричных (т. e. при х° = 0) автоколебании этого контура, взятого отдельно. Затем через величину ас определяется значение kн для данной нелинейности. После этого процесс управления во всей системе в целом исследуется и рассчитывается как в чисто линейной с заменой нелинейности F(x) на kн х ⁰.

Задача 2. Влияние автоколебательных вибрационный помех на устойчивость и качество процесса управлениям

Наряду со специальным использованием автоколебаний, изложенным в задаче 1, могут быть случаи их вредного влияния вплоть до нарушения устойчивости процесса управления. Это влияние совершенно аналогично действию внешних вибрационных помех (лекция 25).

Обратимся к той же задаче учета упругих вибраций корпуса самолета в полете, как и при исследования вибрационной помехоустойчивости в предыдущей лекции. Там эти вибрации считались поступающими на гироскоп извне. Строго же говоря, они имеют место внутри систем мы, как показано на рис. 6.18, а, где автопилот и самолет составляют прежний контур управления, в котором рассматривается движение самолета как твердого тела. Но теперь параллельно ему подключен еще контур упругих колебаний корпуса с уравнением

где 1 — угол отклонения при изгибе оси самолета в точке установки гироскопа. Изгибные вибрации при таком рассмотрении являются автоколебательными.

Чтобы определить коэффициент усиления kн нелиней­ности F(x) автопилота в процессе управления, нужно найти сначала амплитуду симметричных изгибных колебаний ас.

Рис. 6.18.

Поскольку они не проходят через звено «само­лет как твердое тело», то для определения ас рассчиты­ваются автоколебания в отдельном контуре (рис. 6.18, б). Затем полученное значение ас используется при опреде­лении kн, после чего система самолет — автопилот исследуется как линейная с учетом выражения kн че­рез другие параметры системы (см. пример, приводив­шийся выше). Заметим, что поскольку коэффициент демпфирования в уравнении (6.44) мал, то частота автоколебаний будет близка к значению с в уравнении (6.44). Оно и давало возможность рассматривать в предыдущей лекции прохождение автоколебаний через автопилот как прохождение вынужденных колебаний с заданной извне частотой.