В.В.Воробьев. Теория управления. Нелинейные системы автоматического регулирования и управления. Конс / лекция30_31

ЛЕКЦИЯ 30, 31. Нелинейные корректирующие устройства.

План.

1.Отличительные особенности нелинейной коррекции.

2.Система с нелинейной обратной связью.

3.Усовершенствованная система с нелинейной обратной связью.

3. Система с ограничением линейности обратной связи.

Специального вида нелинейности можно вводить в линейную систему в качестве корректирующих устройств; в результате этого в скорректированном виде линейная система становится нелинейной. Коррекцию с помощью нелинейных устройств производят также и в нелинейных системах. Нелинейная коррекция обладает более широкими возможностями, чем линейная, так как она, во-первых, дает большее разнообразие форм частотных ха­рактеристик и, во-вторых, она позволяет менять форму частотных характеристик в зависимости от величины амплитуды сигнала. Последнее свойство нелинейной коррекции является принципиально новым качеством по сравнению с линейной коррекцией. Оно придает системе как бы свойство самонастройки по величине ошибки возникающей в системе в процессе управления.

Задачи нелинейной коррекции могут заключаться, как обычно, в достижении желаемых свойств процессов управления, причем должна предусматриваться возможность изменения этих свойств с изменением величина отклонения. Таким образом, открывается возможности преодолевать известное из линейной теории противоречие между требованиями точности и требованиями устойчивости системы, а также значительно усиливать регулирующее воздействие при больших отклонениях и т. п.

Кроме того, если в заданной нелинейной системе имеются вредные для процесса нелинейности (люфт, гистерезис, зона нечувствительности), то путем введений

Рис. 7.10.

специальной нелинейной коррекция можно в известной мере ослабить вредное влияние имеющихся в системе неизбежных нелинейностей.

В качестве первых примеров рассмотрим введение нелинейного корректирующего устройства в линейную систему.

1. Проанализируем систему с нелинейной обратной связью, сигнал которой уменьшается с возрастанием ошибки. Схема такой системы показана на рис. 7.10. Напряжение, пропорциональное модулю ошибки, подается на вход умножителя и затем вычитается из выходного напряжения тахогенератора, находящегося в цепи линейной обратной связи. Сигнал обратной связи уменьшается, когда ошибка возрастает, что приводит к убыстрению отработки больших отклонений и уменьшению скорости отработки в конце процесса. Динамика системы описывается уравнениями

Уравнение системы в переходном процессе без внеш­него воздействия (1 = 0) имеет вид

где kос = k2 k3 k5, k’ос = k1 kв kос, k = k1 k2 k4. Гармониче­ская линеаризация входящей сюда нелинейности F(x) = хрх для переходного процесса, согласно (6.48), дает

где по формулам (4.11) с учетом (6.47) для данной не­линейности имеем

После интегрирования получаем

Тогда характеристическое уравнение системы (7.12) примет вид

Подстановка  =  + j дает два уравнения

Из второго уравнения

а из первого —-

На основании этих двух формул можно построить диаграммы качества нелинейных переходных процессов (см. лекцию 27) по любому параметру, например по парамет­ру k. Можно также при всех заданных параметрах опре­делить зависимости (а) и (а) и произвести оценки качества переходных процессов.

2. Рассмотрим более совершенную систему, схема ко­торой изображена на рис. 7.11. Система отличается от прежней тем, что сигнал нелинейной коррекции uос проходит через контакты реле. В результате при u5 < 0 (т. е. в четных четвертях колебаний) сигнал нелинейной коррекции не подается на вход усилителя. Это — сущест­венное улучшение в сравнении с предыдущей системой, так как там уменьшение демпфирования давалось во всех четвертях колебаний, в то время как в четных чет­вертях это уменьшение пользы не приносят. Здесь оно исключается за счет отключения коррекции при u5 < 0.

Pис.7.11.

В результате вместо уравнения (7.12) теперь полу­чим

где

Коэффициенты гармонической линеаризации изменят­ся при этом следующим образом:

Подставив это в общую формулу (7.13), получим

Характеристическое уравнение гармонически линеаризо­ванной системы примет вид

После подстановки  = +j отсюда получаются два уравнения. Каждое из них дает возможность выразить величину а в явном виде:

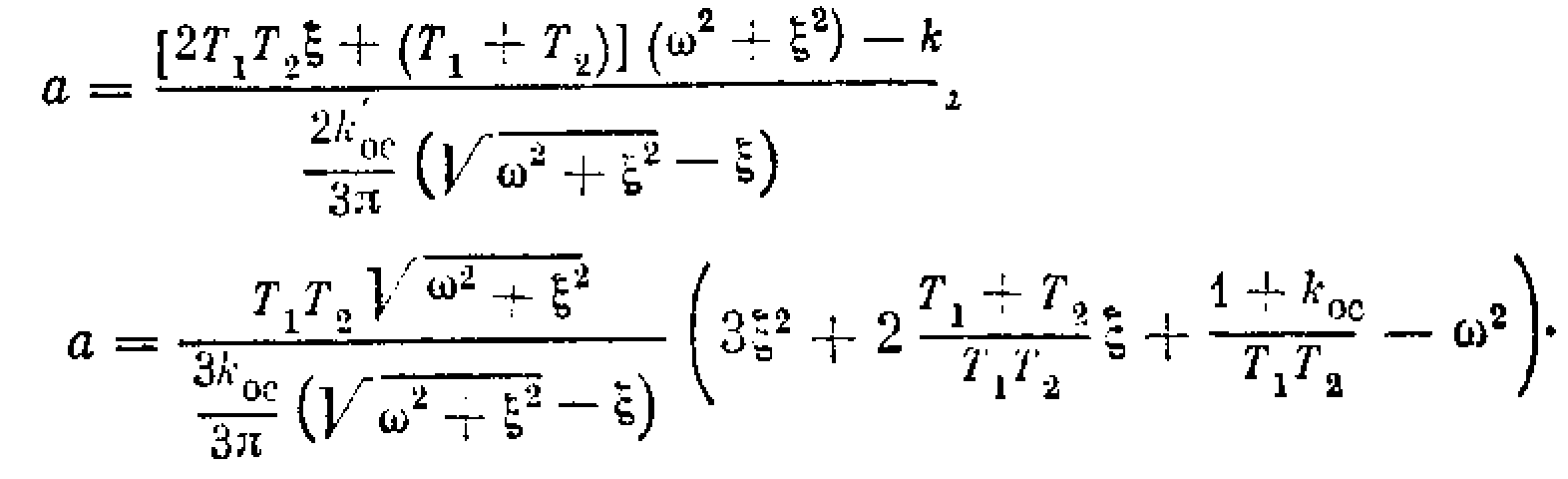
Графическим решением этой системы двух уравнений можно найти значения а и  для каждого заданного значения . В результате получаются зависимости (a) и (а), характеризующие качество переходных процессов при заданных параметрах системы. Если же менять k или другой параметр системы, то можно построить и диаграммы качества нелинейных переходных процес­сов в этой системе по любому параметру.

3. Система с ограничением линейности обратной свя­зи схематически показана на рис. 7.12. Уравнения ее заданы в виде

где F(д) - нелинейность, изображенная на рис. 7.12. Применение такой нелинейной обратной связи позволяет уменьшить величину ошибки в динамике при большой скорости отработки (улучшает качество переходного процесса сохраняя возможность обеспечения необходимого значения kос при малых скоростях, исходя из требования

Рис. 7.12.

статической точности. Гармоническая линеаризация для переходного процесса здесь, согласно лекции 27, дает

причем

Характеристическое уравнение системы:

Из двух уравнений, получаемых после подстановки  =  +j, находим

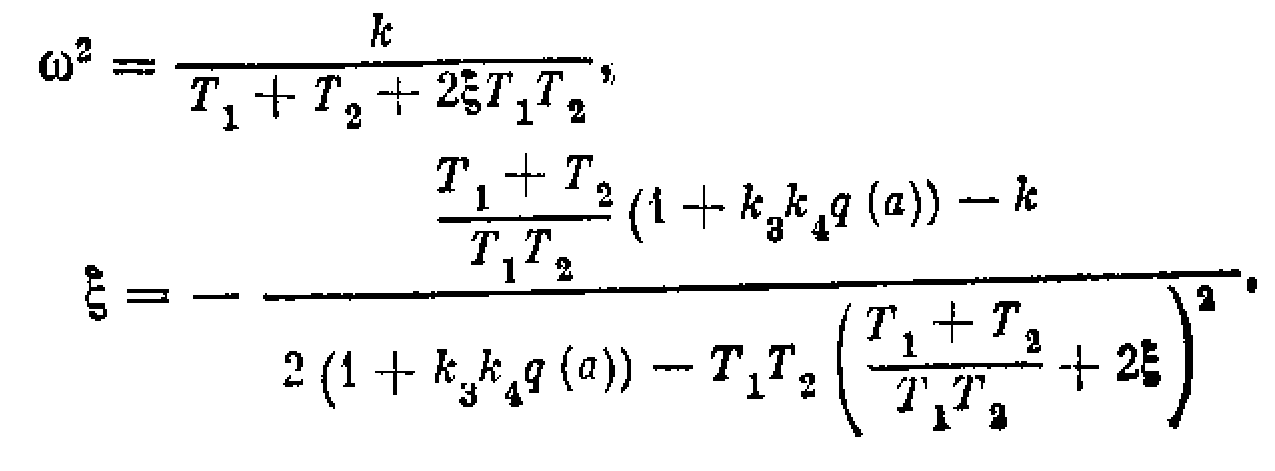
Построим зависимости (а) при разных значение параметра , входящего в выражение для q(a) (7.15) и определяющего зону линейности характеристики обратной связи (рис, 7.12). Эти зависимости (а) показаны

Рис.7.13.

на рис. 7.13. По величине (а) можно составить оценку длительности переходного процесса и выбрать наилучшее значение b.

4. Приведем, наконец пример введения нелинейной коррекции в нелинейную ав­томатическую систему. Схема системы представлена на рис. 7.14. Система имеет релейное управление. В качестве корректирующего уст­ройства введена нелинейная обратная связь по скорости с параболической характеристикой

uос = kос х² sign x, x = p.

После гармонической линеаризации имеем

где ах — амплитуда колебаний скорости х = р. Релейная характеристика

в результате гармонической линеаризации принимает вид

где а - амплитуда колебаний переменной u. Передаточ­ные функции линейных звеньев системы указаны на схеме рис. 7.14.

Характеристическое уравнение гармонически линеа­ризованной системы получает вид

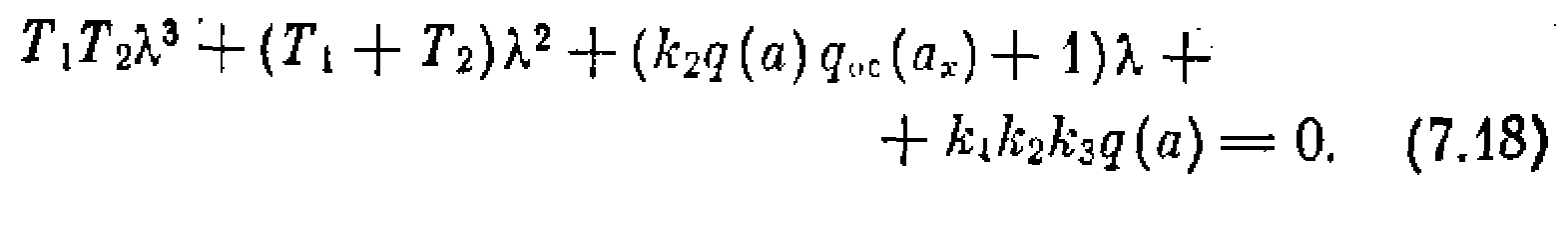
Выразим амплитуду ах, через а. Согласно схеме рис. 7.14 получаем

Тогда по формуле (7.16) получаем

Исследуем устойчивость данной системы с нелиней­ной обратной связью и сравним со случаем, когда, в той же

Рис. 7.14.

релейной системе обратная связь линейна, т. е. когда величина qос заменяется просто коэффициентом kос. Гра­ницу устойчивости будем искать как границу области существования автоколебаний согласно указанию в кон­це лекции 22.

Подставив в характеристическое уравнение (7.18)  = j получим

Эти два уравнения с подстановкой (7.19) определяют частоту  и амплитуду а автоколебаний. Выполнение равенств (7.20) соответствует прохождению кривой Ми­хайлова (при данном значении а) через начало координат (кривая 1 на рис. 7.15). Для устойчивости системы (отсутствие автоколебаний) нужно, однако, чтобы уравнения (7.20) не удовлетворялись и кривая Михайлова охватывала бы начало координат (кривая 2 на рис. 7.15), т.е. чтобы при Х= 0 выполнялось условие Y0(a) > 0 при любом значении а. Удобнее пользоваться выражением

Поскольку параметр  > 0, то данное условие устойчивости

Рис. 7.15.

можно записать в виде

Из условия Х = 0, согласно (7.20) выразим параметр  через величину а: '

и подставим его в выражение для Y(a), используя одновременно и подстановку (7.19). В результате получим условие устойчивости (7.21) в виде

где

В случае, если в данной релейной системе обратная связь линейна, т. е. qос = kос, получим согласно (7.20) более простое выражение условия устойчивости:

или

Отсюда видно, что если

то система устойчива при любых значениях коэффициен­та усиления k2 и сигнала с реле. При

Рис.7.16.

условие (7.24) будет удовлетворено при всех значениях а в том случае, если оно удовлетворяется при наибольшем значении q. График q(а), согласно (7.17), имеет вид, изображенный на рис. 7.16, а условие устойчивости релейной системы с ли­нейной обратной связью (7.24) принимает вид

В соответствии с этим на рис. 7.17 изображена область устойчивости на плоскости k2 kос а случае линейной обратной связи.

Рис. 7.17.

Аналогично на основании выражения (7.23) запишем условие устойчивости релейной системы с нелинейной обратной связью:

Здесь также надо потребовать удовлетворения этого условия при наибольшем значении q(a). Условие устойчивости примет вид

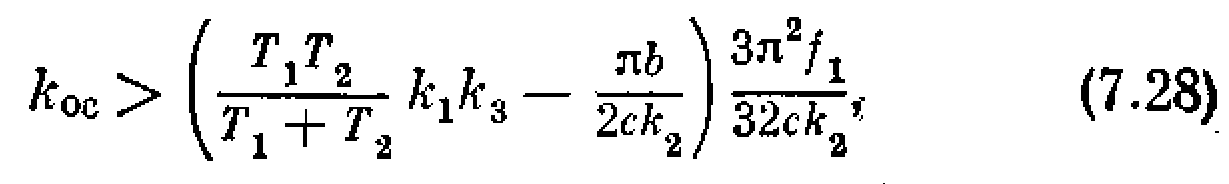
где

Поскольку в первом грубом приближении величина f1 пропорциональна величине сk2, то характер очертания границы устойчивости сохранится. Если при этом множитель за скобкой в выражении (7.28) можно сделать меньшим единицы, то за счет нелинейности обратной связи можно расширить область устойчивости, как показано на рис. 7.17,