В.В.Воробьев. Теория управления. Нелинейные системы автоматического регулирования и управления. Конс / ЛЕКЦИЯ1

ЛЕКЦИЯ 1. Виды и особенности нелинейных систем.

План.

1. 1. Понятие нелинейной системы.

2. Статические нелинейности.

3. Динамические нелинейности.

Система автоматического управления или регулирования называется нелинейной в том случае, если хотя бы одно звено системы описывается нелинейным уравнением (обладает нелинейной характеристикой). В первой части курса изучались линейные системы как обыкновенные, так и другие (с запаздыванием, с распределенными параметрами, с переменными параметрами и дискретные). Система любого из этих видов становится нелинейной, если хотя бы в одном звене систе­мы имеется какое-либо отклонение от линейной зависимости. Поэтому класс возможных нелинейных систем весьма широк.

Строго говоря, все реальные системы являются в большей или меньшей степени нелинейными. Однако во всех случаях, когда с инженерной точки зрения до­пустимо рассматривать линеаризованную систему, обра­щаются к линейной теории как более простой и более разработанной. И только тогда, когда нелинейность иг­рает существенную роль в поведении системы, прибега­ют к теории нелинейных систем. Последняя становится все более важной для практики по мере повышения требований к качеству процессов и к точности расчета систем автоматического управления и регулирования. Можно различать статические и динамические нели­нейности.

Статические нелинейности — это нелинейности стати­ческих характеристик. Они могут быть непрерывными (рис. 1.1), или релейными (рис. 1.2). С другой стороны, они могут быть однозначными (рис. 1.1 и 1.2), петле­выми гистерезисными (рис. 1.3) или опережающими (рис. 1.4). Па рисунках даны примеры аналитического описания статических нелинейностей.

Нелинейные статические характеристики могут иметь и более сложный вид, как это показано, например, на рис. 1.5. а) Комби­нация релейной и линейной характеристик; б) характе­ристика расхода газа х2 при разных давлениях в зависи­мости от открытия клапана х1 в) зависимость скорости

Рис. 1.2.

привода х2 от управляющего сигнала х1 при разных на­грузках; г) зависимость между моментом и угловой ско­ростью электродвигателя при разных напряжениях.

Динамические нелинейности — это нелинейности, связанные с дифференциальными уравнениями динамики звена. К ним относится, например, нелинейное трение. Так, нелинейная сила вязкого трения характеризуется выражением

Сила сухого трения в простейшем случае (имеются и более сложные зависимости) описывается соотношением

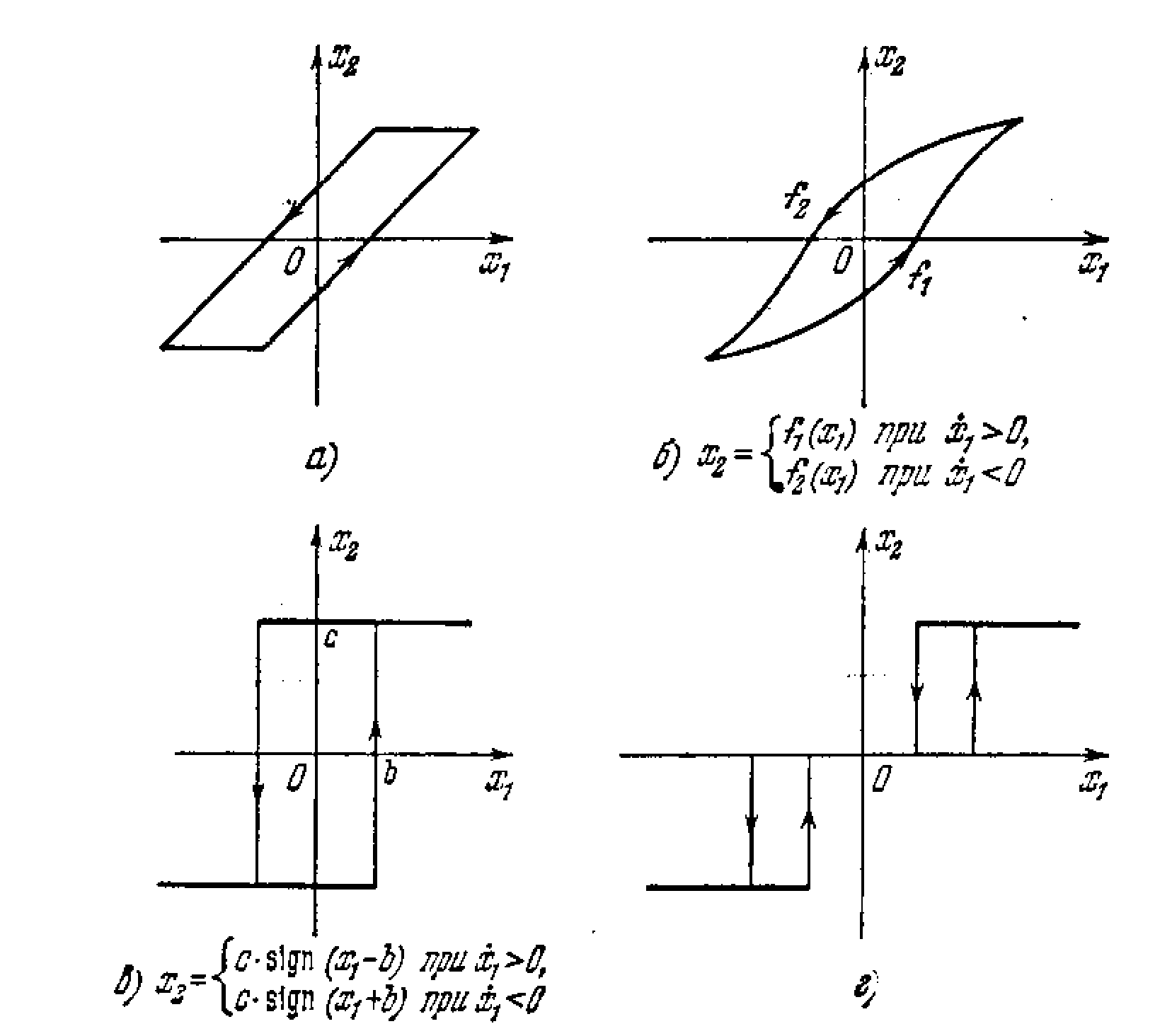
Рис. 1.3.

Звено с изменяющейся постоянной времени имеет вид

или же

Рис. 1.4.

Рис. 1.5.

Здесь надо отметить особенность такой динамической нелинейности по сравнению с линейным звеним с переменным параметром вида

В системе с переменными параметрами фигурирует зави­симость коэффициентов от времени, в то время как нели­нейность характеризует их зависимость от координат (или производных). Точно так же, например, гистерезис (рис. 1.3) представляет собой нелинейное (координатное) запаздывание, в отличие от временного или инерционного в линейных системах. Аналогично на рис. 1.4 представле­но нелинейное (координатное) опережение.

Конечно, -могут быть нелинейные звенья с перемен­ным параметром, например вида

а также нелинейные запаздывающие звенья типа

Примерами динамических нелинейностей могут слу­жить также любые нелинейные дифференциальные, раз­ностные и интегральные уравнения.

Нелинейности в системах управления и регулирования могут быть естественно присущими реальной системе (трение, люфт, гистерезис, зона нечувствительности, насы­щение) и зачастую вредными; влияние их в этом случае надо стремиться уменьшить. Но могут быть и специально вводимые нелинейности для придания системе желаемых свойств. Таковы, например, релейные элементы и различ­ные нелинейные и псевдолинейные корректирующие устройства. Большой интерес представляют также логи­ческие нелинейные управляющие блоки и системы с пе­ременной структурой, о которых речь будет в последую­щих главах. Оптимизация систем автоматического управления также в большинстве случаев связана с введением специальных нелинейностей в контур системы. Введение специальных нелинейностей приводит к различным нелинейным законам управления, которые обладают более богатыми возможностями по сравнению с линейными.