В.В.Воробьев. Теория управления. Нелинейные системы автоматического регулирования и управления. Конс / ЛЕКЦИЯ21

ЛЕКЦИЯ 21. Пример исследования устойчивости методом Ляпунова.

План.

1. Уравнения системы управления курсом самолета.

2. Описание установившегося режима полета.

3. Получение условий устойчивости.

4. Определение областей абсолютной устойчивости в пространстве параметров системы.

В качестве примера исследуем систему управления курсом самолета (рис. 5.9). Уравнение движения самолета в упрощенном виде имеет вид

где  — угол отклонения оси самолета по курсу,  — угол отклонения руля, F(u) —нелинейная характеристика привода руля (рис. 5.10, д), причем

Измерительно-усилительное устройство с обратной связью привода описывается выражением

Для перехода к каноническим уравнениям представим уравнение самолета (5.21) в виде

и обозначим

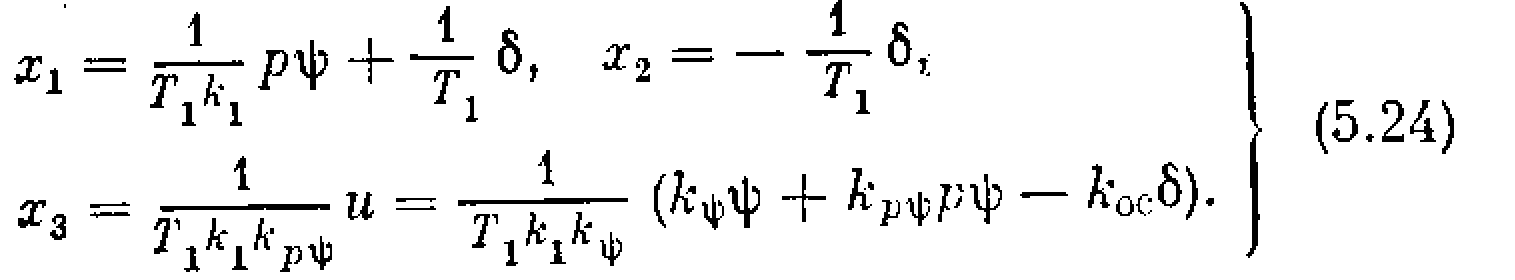
В связи с последним обозначением нелинейная характеристика F(u) заменится на f(х3) (рис. 5.10, б), где

Рис. 5.9.

Рис. 5.10.

изменится лишь масштаб по оси абсцисс. Поэтому зона нечувствительности вместо b (рис. 5.10. а) будет иметь размер b/(T1 k1 k p.)

Введем безразмерное время  = t/T1 . Тогда система уравнений (5.21), (5.23) преобразуется к каноническому виду

Рис.5.11.

где

Как видно из уравнений (5.21)— (5.24), установив­шийся режим полета, устойчи­вость которого надо исследо­вать, определяется значениями  = 0, р=0 < (b/kp) или х1=0, х2=0,х3<(b/T1 k1 kp), что иллюстрируется отрезком АВ на рис. 5.11. Рассмотрим отдельно два случая  > 1 и 0<<1.

1. Случай  >1 Функция Ляпунова берется в виде

Производная от нее

или в силу уравнений системы (5.25) после простых преобразований имеем

Функция V (х) (5.27) является положительно опре­деленной. Производная же W (х) от нее будет отрица­тельной знакопостоянной при условии

г>-1, если >1. (5.28)

Это и является, следовательно, условием устойчивости системы согласно теореме Ляпунова.

Заметим, что dV/d = W (х) обращается в нуль, ког­да х1 = 0 и f (х3) = 0 при любом значении х2, т. е. на всей полосе, изображенной па рис. 5.12. Поэтому инте­ресно проверить, не застрянет ли изображающая точна на этой полосе, если фазовая траектория попадет туда. Из уравнений (5.25) на этой полосе имеем

Следовательно, фазовая траектория будет проходить че­рез полосу в направлении, параллельном оси х3, как показано на рис.5.12. и не застрянет на ней.

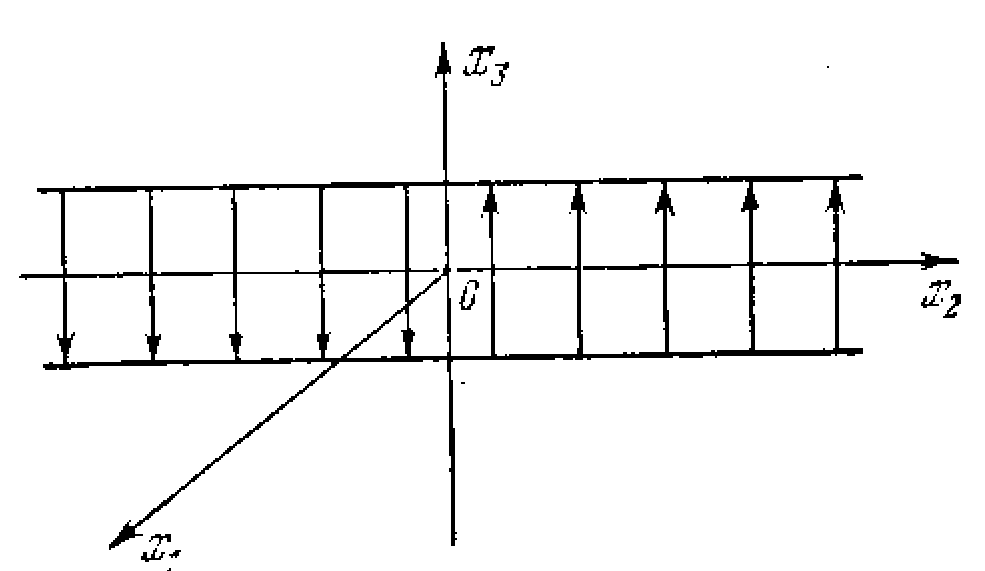
Рис. 5.12.

2. Случай 0<<l. Функция Ляпунова берется в

виде

Производная от неё в силу уравнений системы (5,25):

Отсюда условие устойчивости системы, как условие от­рицательного знакопостоянства функции W (х) прини­мает вид

г > 0, если 0 <  < 1. (5.29)

В соответствии с обозначениями (5,26) через исходные параметры системы условия устойчивости (5,28) и (5.29) запишутся в виде соответственно

что графически изображено на рис. 5.13, а. Этот резуль­тат физически понятен: коэффициент дополнительной обратной связи kос должен быть достаточно большим, если коэффициент интенсивности введения производной от ошибки kр взят сравнительно малым. Устойчивость системы не зависит от величины коэффициента обрат­ной связи, если производная введена с достаточно боль­шим коэффициентом.

Рис. 5.13.

Согласно (5,30) имеем (при положительных коэффи­циентах)

т. е. основной коэффициент усиления автопилота k мож­но увеличить за счет усиления обоих стабилизирующих средств: kос и kр, что показано графически на рис. 5.13, б.

Поскольку в условия устойчивости нелинейной систе­мы (5.30) не вошли параметры самой нелинейности, они являются условиями абсолютной устойчивости системы при любой форме однозначной нелинейности, удовлетво­ряющей лишь условию (5.22).