В.В.Воробьев. Теория управления. Нелинейные системы автоматического регулирования и управления. Конс / ЛЕКЦИЯ24

ПРОЦЕССЫ УПРАВЛЕНИЯ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

В НЕЛИНЕЙНЫХ СИСТЕМАХ

ЛЕКЦИЯ 24. Одночастотные вынужденные колебания. Частотные характеристики.

План.

1. Постановка задачи. Описание неавтономной динамической системы.

2. Условия существования одночастотных вынужденных колебаний.

3. Явление захватывания.

4. Частотные характеристики замкнутой системы по первой гармонике.

Исследование вынужденных колебаний нелинейных систем представляет собой в общем сложную задачу в связи с отсутствием суперпозиции отдельных решений, а также существенным изменением поведения системы в зависимости от размера амплитуды колебаний, с наличием не единственного установившегося режима и возможностью перескоков с одного режима на другой, с особенностями высших гармоник, субгармоник, комбинационных частот и с многими другими факторами.

В данной лекции мы рассмотрим случай одночастотных вынужденных колебаний, т. е. колебаний нелинейной системы с частотой внешнего периодического воздействия, и найдем условия их существования.

Рассмотрим нелинейную систему с внешним воздействием (рис. 6.1), заданным в виде

F(t) = В sin t. (6.1)

Уравнение динамики системы имеет вид

Решение для вынужденных колебаний будем искать приближенно в форме

где  задано, а неизвестными являются амплитуда а и фаза .

Рис.6.1.

Произведем гармоническую линеаризацию нелинейности:

где коэффициенты q(а) и q’(а) вычисляются для сим­метричных (нечетных) нелинейностей по прежним фор­мулам (4.11), если в них положить  = t+. Для конкретных нелинейностей можно здесь использовать формулы, полученные в лекции 13, 14.

Подставим (6.1), (6.3) u (6.4) в уравнение систе­мы (6.2):

Используем символический метод определения периоди­ческого решения, подставив сюда р = j, а вместо sin t выражение е^jt. Тогда полу­чим

или

где

Рис. 6.2.

Уравнение (6.6) с двумя неизвестными а и  можно решить графически, как показано на рис. 6.2. Правая часть (6.6) изображается в виде окружности радиуса В, а левая часть Z(a) строится как кривая по точкам с пе­ременным параметром а. Точки пересечения окружности с кривой Z(a) дают решение, причем величина ампли­туды вынужденных колебаний определяется в точке пересечения по отметкам на кривой Z, а фаза—но вели­чине угла (рис. 6.2).

На рис. 6.2 окружности пересекают кривую только при радиусе большем некоторого порогового значения В >Впор- Следовательно, в этом случае одночастотные вынужденные колебания (6.3) возможны только при

Рис. 6.3.

Pиc.6.4.

достаточно большой амплитуде В, а при меньшей ампли­туде В внешнего воздействия будет иметь место сложное движение, включающее в себя и собственную частоту системы.

Построив серию кривых Z(a) по формуле (6.7) для разных значений частоты внешнего воздействия  (рис. 6.3), можем построить график зависимости поро­гового значения В от частоты , например, в виде, изоб­раженной на рис. 6.4, где а — частота автоколебаний данной системы. Тогда мы получим область значений В и а, в которой существуют одночастотные вынужденные колебания. Эта область называется областью захватывания. Явление захватывания состоит в том, что при В > Впор собственные колеба­ния (автоколебания) срывают­ся и система переходит целиком на одночастотные вынужденные колебания с частотой внешнего воздействия. Строго говоря, эти одночастотные вынужденные колебания будут несинусоидальными. В соответствии со свойством фильтра линейной части (лекция 12) они для перемен­ной х будут только близки к синусоидальным (6.3). Об определении­

Рис. 6.5.

высших гармоник этих колебаний.

На основании рис. 6.3 можно построить зависимости а() и (), т. е. частотные характеристики замкнутой нелинейной системы по первой гармонике (6.3). В ли­нейных системах частотные характеристики А() и () не зависели от размера входной амплитуды и вычисля­лись для единичной амплитуды на входе. В нелинейной же системе характер частотных характеристик А()=а ()/B и () может существенно зависеть от раз­мера В. Поэтому для разных значений В получается се­рия частотных характеристик (рис. 6.5) замкнутой сис­темы по первой гармонике.

Пример. Пусть уравнение системы имеет вид

при гистерезисной нелинейности (рис. 6.6) и f(t) = B sin t. Тогда в уравнении (6.6), согласно (6.7), бу­дем иметь

Для заданной частоты  = 10 сек ^-1 и заданных пара­метров системы k = 10, с = 10, b = 4, Т1 = 0,01, T2 =0,02, кривая Z(a) изображена на рис. 6.6, где отмечены

Рис.6.6.

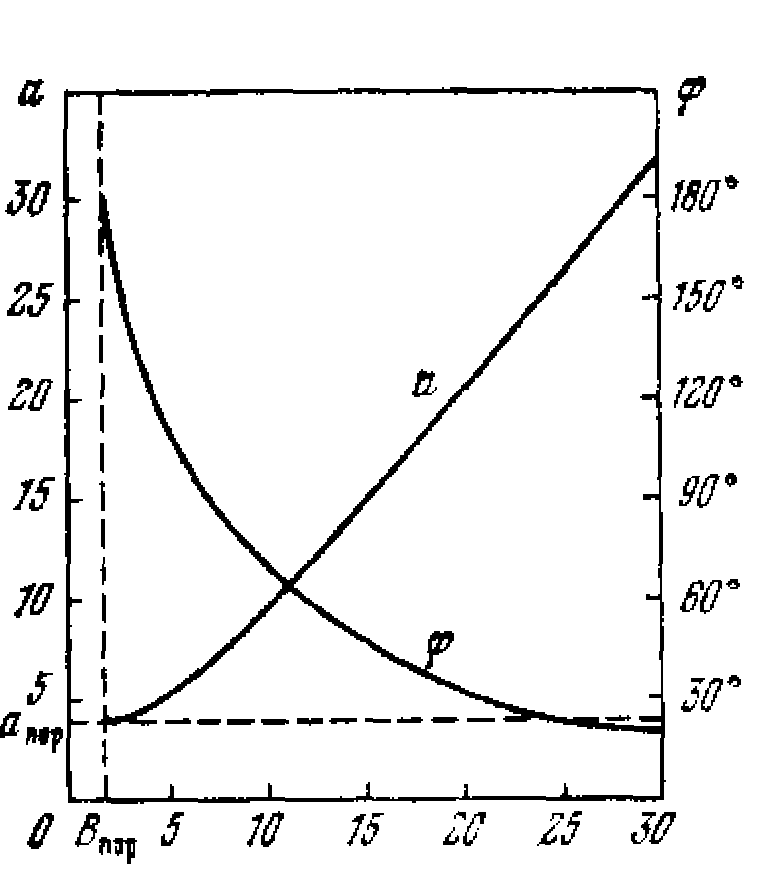
Рис. 6.7.

значения а. Проведя окружности разных радиу­сов В, по точкам пересечения определим зависимости а (В) и (В) (рис. 6.7) для вынужденных колебаний при данной частоте.