- •Министерство образования и науки Российской Федерации
- •Содержание
- •Введение
- •1. Современное состояние проблемы моделирования систем
- •1.1. Моделирование как метод научного познания. Философские аспекты моделирования
- •1.2. Использование моделирования при исследовании и проектировании систем
- •1.2.1. Особенности разработки систем
- •1.2.2. Особенности использования моделей
- •1.2.3. Перспективы развития методов и средств моделирования систем
- •2. Основные понятия теории моделирования систем
- •2.1. Принцип системного подхода в моделировании систем
- •2.1.1. Структура системы – совокупность связей между элементами системы
- •2.1.2. Экспериментальные исследования систем
- •2.2. Стадии разработки моделей
- •2.3. Понятие подобия
- •2.3.1. Общие положения
- •2.3.2. Основные понятия теории размерности
- •2.3.3. Примеры подобия
- •2.4. Общая характеристика проблемы моделирования систем
- •2.4.1. Объект моделирования.
- •2.4.2. Характеристики моделей систем
- •2.4.3. Цели моделирования систем
- •2.5. Классификация видов и методов моделирования систем
- •2.5.1. Классификационные признаки
- •2.5.2. Математическое моделирование.
- •2.6. Построение модели
- •2.7. Разработка вычислительного метода
- •2.8. Проверка (тестирование) модели
- •3. Математическое моделирование
- •3.1. Задачи и цели исследования математических моделей
- •3.2. Методология математического моделирования. Системный анализ
- •3.2.1. Понятие системы
- •3.2.2. Этапы системного анализа и декомпозиция
- •3.2.3. Экспертные оценки
- •3.3. Классификация математических моделей
- •3.4. Методы формализованного описания системы
- •3.4.1. Математическая модель по “входу-выходу”
- •3.4.2. Математическая модель в пространстве состояний
- •3.4.3. Описание линейных систем в пространстве состояний
- •3.4.4. Реализация систем в пространстве состояний
- •3.5. Методы построения математических моделей и их применение в сапр
- •3.5.1. Методы построения математических моделей
- •3.5.2. Математические модели с точки зрения сапр
- •3.5.4. Методика составления уравнений динамики элементов сау
- •3.6. Математические модели системы управления. Понятие об оптимальном управлении
- •4. Экспериментальное определение динамических характеристик объектов моделирования
- •4.1. Понятие о динамических характеристиках объектов
- •4.2. Определение динамических характеристик элементов систем по временным характеристикам
- •4.2.1. Определение статических характеристик
- •4.2.2. Определение динамических характеристик объектов с помощью периодических воздействий
- •4.4.1. Временные характеристики и их свойства
- •4.4.2. Определение характеристик апериодического звена
- •4.4.3. Определение характеристик колебательного звена
- •4.3. Формы описания динамических свойств объектов
- •4.4. Синтез пассивных двухполюсников и четырехполюсников
- •4.3.1. Разложение передаточной функции активного четырехполюсника
- •4.3.2. Способы синтеза двухполюсников
- •4.5. Экспериментальная отработка характеристик системы управления движущимся объектом
- •4.5.1. Общие положения
- •4.5.2. Алгоритмы обработки внешнетраекторных измерений
- •5. Динамические свойства воспринимающих элементов и датчиков
- •5.1. Основные определения и понятия
- •5.1.1. Понятие датчика
- •5.1.2. Классификация датчиков
- •5.2. Основные характеристики датчиков
- •5.2.1. Погрешности измерений
- •5.2.2. Чувствительность датчиков
- •5.2.3. Быстродействие датчика
- •5.3. Схемы формирования сигналов пассивных датчиков
- •5.3.1. Общие характеристики
- •5.4. Оптические датчики
- •5.4.1. Определения и основные зависимости
- •5.4.2. Фоторезисторы
- •5.4.3. Фотодиоды
- •5.4.4. Тепловые приемники излучения
- •5.4.5. Датчики изображения
- •5.4.6. Волоконная оптика
- •5.5. Датчики температуры
- •5.5.1. Методы измерения температуры
- •5.6. Датчики положения и перемещения
- •5.6.1. Методы определения положения и перемещения
- •5.6.2. Резисторные потенциометры
- •5.6.3. Индуктивные датчики
- •5.6.4. Емкостные датчики
- •5.6.5. Цифровые датчики
- •5.6.6. Датчики близости
- •5.7. Датчики деформации
- •5.7.1. Основные определения
- •5.7.2. Основные положения
- •5.8. Тахометрические датчики
- •5.8.1. Электродинамическая тахометрия
- •5.8.2. Импульсная тахометрия
- •5.8.3. Гирометры
- •5.9. Датчики ускорения, вибрации и удара
- •5.9.1. Общие положения
- •5.9.2. Принцип действия сейсмических датчиков
- •5.10. Датчики скорости, расхода и уровня жидкости
- •5.10.1. Элементарные понятия
- •5.10.2 Датчики и методы измерения скорости жидкости
- •5.10.3. Измерение расхода жидкости
- •5.10.4. Измерение и указание уровня жидкости
- •5.11. Датчики влажности
- •5.11.1. Определения
- •5.11.2. Гигрометры
- •5.12. Акустические датчики
- •5.12.1. Распространение плоской волны
- •5.12.2. Распространение трехмерной волны
- •5.12.3. Микрофоны
- •5.12.4. Измерение интенсивности
- •6. Основы технологии имитационного моделирования
- •6.1. Основные определения и понятия
- •6.2. Область применения и классификация имитационных моделей
- •6.3. Описание поведения системы
- •6.3.1. Общие положения.
- •6.3.2. Методика моделирования случайных факторов
- •6.3.3. Два подхода к моделированию случайных чисел
- •6.4. Оценка качества псевдослучайных чисел
- •6.5. Оценка качества имитационного моделирования
- •7. Методы испытаний систем управления и их применение в системах автоматизированного проектирования (сапр)
- •7.1. Полунатурное моделирование
- •7.1.1. Общие положения
- •7.1.2. Автоматизация испытаний на основе полунатурного моделирования
- •8. Анализ систем управления с эвм
- •8.1. Основные задачи
- •8.2. Особенности систем управления с эвм
- •8.2. Основные положения из теории дискретных линейных систем
- •8.2.1. Последовательности
- •8.2.2. Линейные системы с постоянными параметрами
- •8.2.3. Разностные уравнения
- •8.2.3.1. Решение разностных уравнений методом прямой подстановки
- •8.3. Расчет цифровых фильтров по фильтрам непрерывного времени
- •8.3.1 Методика синтеза цифровых фильтров. Общие положения
- •8.3.2 Методы дискретизации аналоговых фильтров
- •8.3.3. Геометрическая интерпретация методов расчета цифровых фильтров по фильтрам непрерывного времени
- •9. Моделирование свойств объектов с помощью системыMatLab
- •9.1. Введение
- •9.2. MatLab как научный калькулятор
- •9.2.1. Командное окно
- •9.2.2. Операции с числами
- •9.2.3. Простейшие операции с векторами и матрицами
- •9.2.4. Некоторые функции прикладной численной математики
- •9.2.5. Построение простейших графиков
- •9.3. Исследование линейных стационарных систем (лсс)
- •9.3.1. Классы пакета control.L
- •9.3.2. Ввод и преобразование моделей
- •Пример создания модели
- •9.3.3. Анализ системы
- •9.4. Моделирование динамических процессов с помощью подсистемы MatLab simulink
- •9.4.1. Краткие сведения о подсистеме MatLab simulink
- •9.4.2. Запуск подсистемы simulink
- •9.4.3. Создание модели
- •9.4.4. Некоторые основные приемы подготовки и редактирования модели
- •9.4.5. Установка параметров моделирования и его выполнение
- •9.2.2. Результат составления модели
- •Приложения п1. Динамические характеристики объектов моделирования
- •П2. Примеры составление функциональной и структурной схемы динамической системы
- •П2.1. Система управления угловой скорости вращения ротора двигателя при условии действия постоянного возмущения
- •П2.2. Система сопровождения цели
- •П2.3. Система автоматического наведения летательного аппарата на объект
- •П2.4. Система управления уровнем жидкости
- •П2.5. Система управления экономическими параметрами
- •Использованные источники
- •Основы теории и практики моделирования динамических систем
9.3.3. Анализ системы
Пакет CONTROL предоставляет пакет процедур для осуществления анализа САУ, прежде всего, для определения отклика системы на внешние воздействия как во временной, так и в частотной областях.
Для нахождения временных откликов системы на внешние воздействия некоторых видов предусмотрены функции:
impulse Нахождение отклика на импульсное входное воздействие.
step Нахождение реакции системы на единичный скачок входного воздействия.
initial Определение собственного движения системы при произвольных начальных условиях.
lsim Определение реакции системы на входное воздействие произвольной формы, задаваемое в виде вектора его значений во времени.
Группа процедур для представления реакции системы на гармонические воздействия в частотной области:
bode Строит график АЧХ и ФЧХ (диаграмму Боде) указанной системы.
nyquist Строит в комплексной плоскости график АФХ разомкнутой системы в полярных декартовых координатах.
nichols Строит карту Николса системы, т.е. график АФХ разомкнутой системы в декартовых координатах.
sigma Строит график зависимости от частоты сингулярных значений системы; обычно совпадает с АЧХ системы.
margin Строит диаграмму Боде с указанием запасов по амплитуде и по фазе.
Процедуры, вычисляющие отдельные характеристики и графически показывающие расположение полюсов и нулей системы.
pole Расчет полюсов системы.
zpkdata Расчет полюсов, нулей и коэффициента передачи системы.
pzmap Построение на комплексной плоскости карты расположения нулей и полюсов системы.
Примеры анализа во временной области
1 .
Применяя процедуруstep
к созданной выше модели,
.
Применяя процедуруstep
к созданной выше модели,
>> step(sys)
можно получить график
2. Аналогично, использование процедуры impulse
>> impulse(sys)
приведет к появлению в графическом окне графика, приведенного ниже:

3. При применении процедуры initial необходимо в число входных параметров включить, во-первых, полный вектор всех начальных условий по переменным состояния, а, во-вторых, момент времени окончания процесса интегрирования.
>> sssys=ss(sys)
>> initial(sssys,[0 0 0 1],20)
Получим

4 .
Для применения процедурыlsim
необходимо
предварительно задать вектор t
значений времени, в которых будут заданы
значения входного воздействия, а затем
задать вектор u
значений входной величины в указанные
моменты времени
.
Для применения процедурыlsim
необходимо
предварительно задать вектор t
значений времени, в которых будут заданы
значения входного воздействия, а затем
задать вектор u
значений входной величины в указанные
моменты времени
>> t=0:0.01:40; u=sin(t); lsim(sssys,u,t);grid
Р езультат
представлен на следующей фигуре:
езультат
представлен на следующей фигуре:
Примеры анализа в частотной области
1. >> bode(sys)
2. >> nyquist(sys)

3. >> nichols(sys)
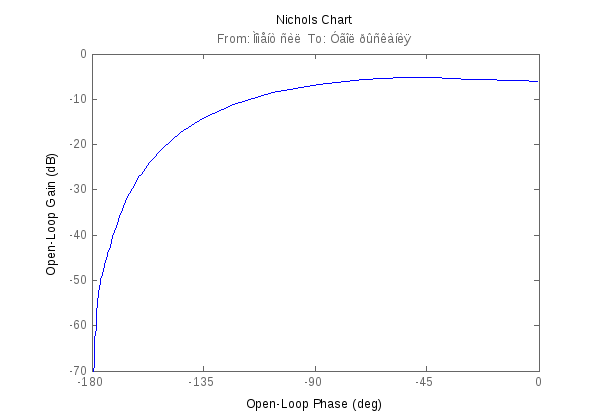
4. >> sigma(sys)

5. >> margin(sys);grid

Примеры применения процедур для вычисления полюсов и нулей системы.
1. >> pole(sys)
ans =
-4.8653 + 8.5924i
-4.8653 - 8.5924i
-0.3847 + 0.6040i
-0.3847 - 0.6040i
2. >> sysz=zpk(sys)
Zero/pole/gain from input "Момент сил" to output "Угол рыскания":
0.25 (s^2 + 10s + 100)
------------------------------------------------
(s^2 + 0.7693s + 0.5128) (s^2 + 9.731s + 97.5)
3. >> [z,p,k]=zpkdata(sysz,'v')
z =
-5.0000 + 8.6603i
-5.0000 - 8.6603i
p =
-4.8653 + 8.5924i
-4.8653 - 8.5924i
-0.3847 + 0.6040i
-0.3847 - 0.6040i
k =
0.2500
4. >> pzmap(sys); grid
Результат представлен на рисунке ниже